Merge Sort(합병정렬)
합병 정렬 또는 병합 정렬은 O(n log n) 비교 기반 정렬 알고리즘이다. 일반적인 방법으로 구현했을 때 이 정렬은 안정 정렬에 속하며, 분할 정복 알고리즘의 하나이다. 존 폰 노이만이 1945년에 개발했다. 위키백과
•
안정 정렬
•
분할 정복 알고리즘
◦
분할 정복 알고리즘(divide and conquer)은
▪
문제를 작은 2개의 문제로 분리해 각각 해결한 후, 결과를 모아 원래의 문제를 해결하는 전략
▪
보통 순환 호출을 통해 구현
1.
리스트의 길이가 0또는 1이면 이미 정렬된 것으로 봄
2.
리스트 길이가 2 이상이라면 리스트를 절반으로 나누어 비슷한 크기의 두 부분리스트로 나눔
3.
각 부분 리스트를 재귀적으로 합병정렬로 정렬
4.
두 부분 리스트를 다시 하나의 정렬된 리스트로 합병
합병정렬 알고리즘
•
분할
•
정복
•
결합
이 세가지 단계로 이뤄짐
ex1)
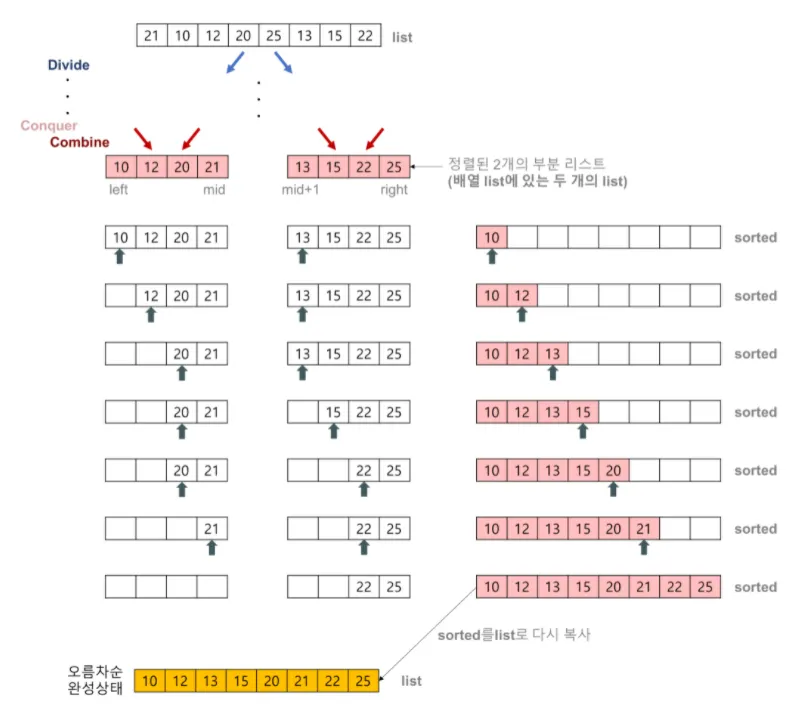
[21, 10, 12, 20, 25, 13, 15, 22] 배열이 있다고 할 때,
1.
2개의 리스트의 값들을 처음부터 하나씩 비교하여 두 개의 리스트의 값 중에서 더 작은 값을 새로운 리스트(sorted)로 옮긴다.
2.
둘 중에서 하나가 끝날 때까지 이 과정을 되풀이한다.
3.
만약 둘 중에서 하나의 리스트가 먼저 끝나게 되면 나머지 리스트의 값들을 전부 새로운 리스트(sorted)로 복사한다.
4.
새로운 리스트(sorted)를 원래의 리스트(list)로 옮긴다.
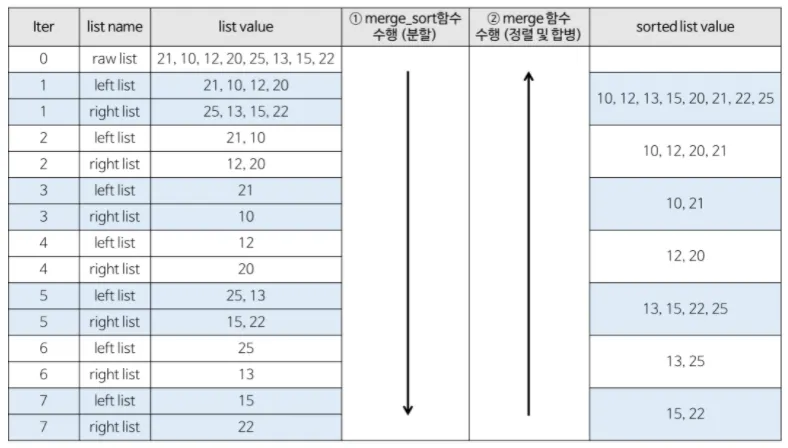
ex2)
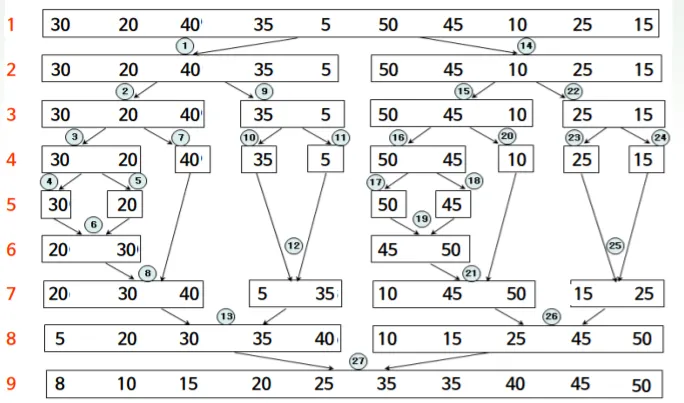
파란 동그라미가 순서를 나타냄
그림처럼 부분리스트 크기가 1이 될 때 까지 분할합니다(단계 5까지)
이후 합병하며 정렬을 하게되는데, 순서가 중요합니다
합병의 순서는 분할의 역순이라고 할 수 있겠습니다.
그림에서 보면 5단계의 맨 앞에 보이는 30, 20이 가장 마지막에 분할되었으므로 맨 처음으로 합병해줍니다.
합병을 하는거는 합병 대상인 두 리스트의 원소를 앞에서부터 비교하여 작은 값을 갖는 원소를 새로운 리스트에 넣어주는 방식으로 생각하면 됩니다.
합병정렬 구현
void MergeSort(int A[ ], int Left, int Right)
/* 입력: A[Left:Right], Left, Right
출력: A[Left:Right] - 정렬된 배열. */
{ int Mid;
if (Left < Right) {
Mid = (Left + Right)/2;
MergeSort(A[ ], Left, Mid);
MergeSort(A[ ], Mid+1, Right);
Merge(A[ ], Left, Mid, Right);
} }
void Merge(int A[ ], int Left, int Mid, int Right)
/* 입력: A[Left:Mid], A[Mid+1:Right] - 정렬된 두 배열.
출력: A[Left:Right] : A[Left:Mid]와 A[Mid+1:Right] 를 합병 */
{ int B[NUM_OF_KEYS], i, LeftPtr, RightPtr, BufPtr;
LeftPtr = Left; RightPtr = Mid + 1; BufPtr = Left;
// 분할 정렬된 list 합병
while (LeftPtr <= Mid && RightPtr <= Right){
if (A[LeftPtr] < A[RightPtr])
B[BufPtr++] = A[LeftPtr++];
else
B[BufPtr++] = A[RightPtr++];
}
// 남은 값 일괄 복사
if (LeftPtr > Mid) {
for (i = RightPtr; i <= Right; i++)
B[BufPtr++] = A[i];
}
// 남은 값 일괄 복사
else{
for (i = LeftPtr; i <= Mid; i++)
B[BufPtr++] = A[i];
}
// 임시배열 B의 리스트를 원래 배열 A로 재복사
for (i = Left; i <= Right; i++)
A[i] = B[i]; }
C
복사
void main(){
int i;
int n = 8;
int list[n] = {21, 10, 12, 20, 25, 13, 15, 22};
// 합병 정렬 수행(left: 배열의 시작 = 0, right: 배열의 끝 = 7)
merge_sort(list, 0, n-1);
}
}
C
복사
단점
•
만약 레코드를 배열(Array)로 구성하면, 임시 배열이 필요하다.(입력 크기에 비례하는)
⇒ 제자리 정렬(in-place sorting)이 아니다.
•
레크드들의 크기가 큰 경우에는 이동 횟수가 많으므로 매우 큰 시간적 낭비를 초래한다.
장점
•
안정적인 정렬 방법 (순차적으로 이동하기 때문에)
•
데이터의 분포에 영향을 덜 받는다. 즉, 입력 데이터가 무엇이든 간에 정렬되는 시간은 동일하다. (로 동일)
•
만약 레코드를 연결 리스트(Linked List)로 구성하면, 링크 인덱스만 변경되므로 데이터의 이동은 무시할 수 있을 정도로 작아진다.
⇒ 제자리 정렬(in-place sorting)로 구현할 수 있다.
•
따라서 크기가 큰 레코드를 정렬할 경우에 연결 리스트를 사용한다면, 합병 정렬은 퀵 정렬을 포함한 다른 어떤 졍렬 방법보다 효율적이다.
[시간복잡도]
Merge함수
•
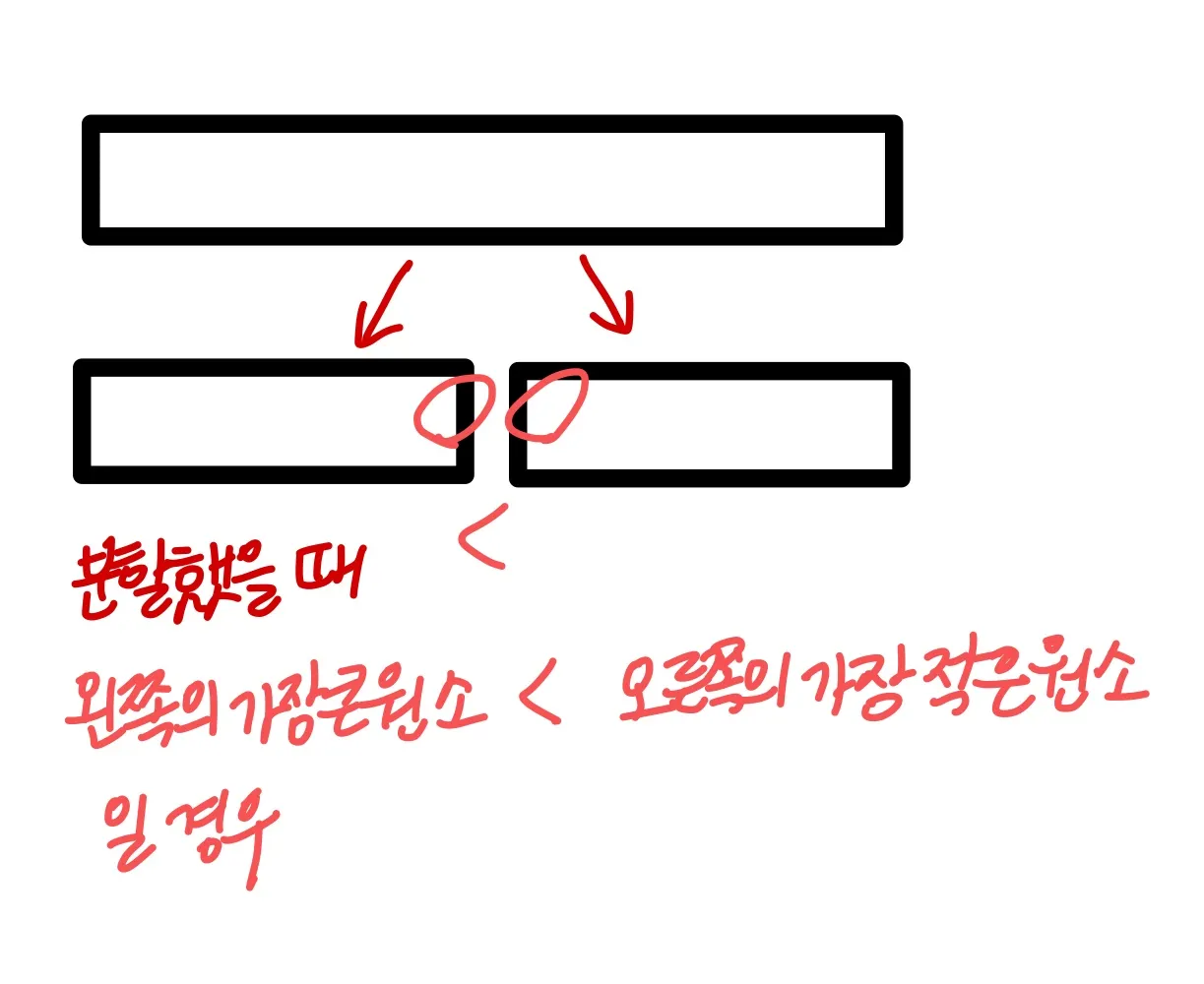
최선시간복잡도 = min(m, n) :
이 때 왼쪽 배열의 모든 원소가 오른쪽 배열의 모든 원소보다 작기 때문에
왼쪽 배열 크기 m, 오른쪽 배열 크기 n일 경우 오른쪽 배열의 첫번째 원소가 왼쪽 배열의 모든 원소와 한번씩 비교가 이뤄진 뒤 더 이상의 비교는 진행되지 않고 복사하는 과정만 이뤄지기 때문이다.
ex) 2, 3, 4, 0, 1 | 7, 8, 9, 5, 6
•
최악시간복잡도 = m+n-1
ex) m=n일때,
a1, a2, ..., am, b1, b2, ..., .bn에 대해
정렬순서가 a1,b1, a2, b2, ..., am, bm인 경우
ex) 0 8 4 2 6 | 1 9 5 3 7
MergeSort함수
•
별도의 배열 B를 사용하므로 제자리 정렬이 아니다(Merge함수에서 입력크기에 비례하는 메모리를 사용하기 때문)
•
안정성 O
•
최악시간복잡도 =
ex) 0 8 4 2 6 1 9 5 3 7
N개의 데이터가 주어져있다면
절반-절반-절반 해가다가 1의 크기 갖는 리스트로 분할때까지 즉, 의 깊이가 발생하고 합병은 역순을 따르기 때문에 그 또한 의 깊이를 갖게되기 때문. (두번의 과정)