선택(Selection)문제

배열에서 i번째 큰 원소 찾기 문제

선택 문제

임의로 나열된 n개의 데이터에서 크기가 i번째인 것을 찾기

•

i=1 : 최소치 문제

•

i=n : 최대치 문제

→ 이 둘은

O(n)

의 복잡도를 가짐

이 외의 일반적인 경우에는 정렬 후 i번째 원소를 선택하게 되어있다.

⇒

O(n\log(n))

: 일반적인 정렬 알고리즘의 시간복잡도

최솟값 찾기 $O(n)$

같은 방식으로 최댓값 찾기도 할 수 있겠죠?

int Minumum (int A[], int n){
	/* 입력A[] : n개의 숫자 저장된 배열
				 n : 배열 A에 저장되어 있는 숫자 개수
		 출력 : A에 저장된 값 중 최솟값 */
	int i, Temp;
	Temp = A[0]; // 맨 첫번째 원소를 Temp에 저장
	for (i=1;i<n;i++)
		if (Temp>A[i]) Temp=A[i]; // A[1]~A[n-1]을 반복하면서, A[i]가 Temp보다 작으면 Temp에 A[i]를 넣음
		// 결과적으로 원소를 하나하나 보면서 비교해서 가장 작은 것을 Temp에 넣게 되는 것
		// O(n)이 걸릴 수 밖에 없다.
	return Temp;
}
C
복사

최댓값 최솟값 동시에 찾기 $O(n)$

선택 알고리즘(Selection algorithm)

void findMinMax(int A[], int n, int *Minimum,int *Maximum){
	/* 입력 A : n개의 숫자 저장되 배열
		 n : 배열 A에 저장되어 있는 숫자 개수
		 출력 : *Minimum A에 저장된 값 중 최솟값 
						*Maximum A에 저장된 값 중 최댓값 */
	int i;
	int Small, Large;
	*Minimum=A[0]; *Maximum=A[0]; // 일단 처음에는 둘 다 A의 첫번째 원소를 넣어준다
	for(i=1,i<n-1;i+=2){
		if (A[i] < A[i+1])
			{Small=A[i]; Large=A[i+1];}
		else
			{Small=A[i+1]; Large=A[i];}
		if(Small<*Minimum) *Minimum=Small;
		if(Large>*Maximum) *Maximum=Large;
	}
	return;
}
C
복사

최댓값 찾기와 최솟값 찾기 방법을 사용한 경우와 선택 알고리즘 사용 경우 비교

(1) 최댓값 찾기 + 최솟값 찾기 시간복잡도 : 최댓값 찾기는 n-1회 비교, 최솟값 찾기는 찾은 최댓값을 제외해 n-2회 비교 :

2n-3

(2) 선택알고리즘 :

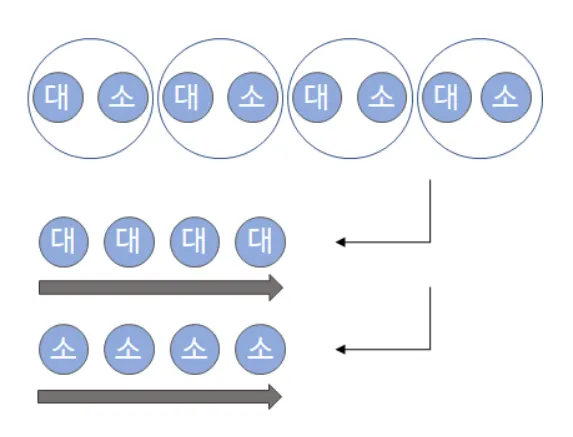
이 방법은 주어진 배열의 요소를 2개씩 묶어 묶음 별로 최대와 최소를 구하는 것이다. (요소가 두개니까 최대 최소라기보다는 더 큰 값, 더 작은 값이겠다 ㅎㅎ)

이렇게 모인 큰 값끼리 비교하고, 작은 값끼리 비교하는 방법이라고 볼 수 있다.

\frac{n-1}{2}

회 반복하고 그 내에서 3번을 비교하게 되므로

시간복잡도 :

\frac{n-1}{2}\times 3 = 1.5n+상수

가 된다. 결국 이것도

O(n)

선택문제 Quick Select

<퀵정렬 관련 내용 : >

퀵정렬 코드구현

void swap(int* a, int* b)
{
	int temp = *a;
	*a = *b;
	*b = temp;
}

int Partition(int A[], int Left, int Right)
{
	// A[Left] : 분할 원소(분할 기준이 되는 원소)
	int PartElem, Value;
	PartElem = Left;
	Value = A[PartElem];
	do
		do while(A[++Left] < Value);
		do while(A[--Right] > value);
		if (Left < Right) Swap(&A[Left], &A[Right]);
		else break;
	while(1);
	A[PartElem] = A[Right];
	A[Right] = Value;
	return Right;
}

 void QuickSort(int A[], int Left, int Right)
{
	int k; // position of partition
	if (Right > Left)
		k = Partition(A[], Left, Right+1;)
		QuickSort(A[], Left, k-1);
		QuickSort(A[], k+1, Right);
}
C
복사

퀵 정렬의 Partition() 함수를 i번째 큰 원소가 나올 때 까지 반복해서 이용하는 방식입니다.

한마디로 pivot과 작은값, 같은값, 큰값으로 나눠 찾고자 하는 수가 어디 속해있을지 찾아나가는 것입니다.

< n개의 값 중 k번째로 크거나/작은 수를 찾는 선택 문제를 Quick Select로 해결하기 >

Pivot 고르기

pivot보다 작은값 배열, pivot보다 큰 값 배열, pivot과 같은 값 배열 새 부분을 나눕니다

찾고자 하는 값 k가 어디에 속해있는지 찾습니다

⇒ 평균 시간복잡도는

O(n)

, 최악 시간 복잡도는

O(n^2)

int Selection_N2(int A[], int n, int i){
	/* 입력 A[] : 입력 데이터 배열, i: 찾는 위치
		 출력 : i번째 숫자의 값 		*/
	int Left, Right, j;
	A[n] = Infinity; // 무한대값을 넣어준다 - 더미 원소
	Left = 0; Right = n;
	while (1){
		j=Partition(A, Left, Right); // Partition은 return Right
		// j는 현재 pivot이 있어야 할 위치가 됨
		// 인덱스는 번째수보다 1작으니까( 0부터 시작하니까 )
		if(i==j+1) return A[j]; // pivot이 찾고자하는 것인 경우
		if(i<j+1) Right=j; // 찾고자 하는 것이 왼쪽( pivot보다 작은 것들)에 있는 경우
		else Left=j+1 // 찾고자 하는 것이 오른쪽( Pivot보다 큰 것들)에 있는 경우
	}
}
C
복사

Best case

O(n)

피벗을 기준으로 양쪽이 균등하게 나눠진다면 나누어진 절반 중에서만 찾으면 되니까 T(n/2), 분배하는 횟수를 n으로 생각하면

T(n) = T(\frac{n}{2}) + n

로 생각할 수 있고, 절반의 절반을 또 찾으면 되니까

T(n/2) = T(n/2^2) + n/2

⇒

T(n) = T(n/2) + n\\ = T(n/2^2 + n/2) + n\\ = T(n/2^k) + n/2^{(k-1)} + ... + n/2 + n

이때 n = 2^k로 가정하면, T(n/2^k) = T(1) = 1 로 생각하고 지워버릴 수 있습니다. 그러면

T(n) = T(n/2) + n\\ = T(n/2^2 + n/2) + n\\ = T(n/2^k) + n/2^{(k-1)} + ... + n/2 + n\\ = n(1 + 1/2 + 1/2^2 + ... + 1/2^k)

가 되고 이때

(1 + 1/2 + 1/2^2 + ... + 1/2^k)

부분은 1에 가깝습니다

따라서 O(n) 의 시간복잡도로 생각할 수 있습니다.

Worst case

O(n^2)

피벗을 기준으로 한쪽으로 모두 치우쳐져 있다면

최악의 경우엔

T(n) = T(n-1) + n

이 되므로 최악의 경우

n^2

을 돌아야합니다.

Average O(n)

하지만 이 경우는 극히 드물기 때문에 Quick Select은 평균적으로

O(n)

으로 생각할 수 있다고 합니다.

Quick Select를 $O(n)$ 으로 구현하기

Median of Medians 알고리즘을 사용하는 것으로, Intro Select라고도 한다.

good pivot을 worst-case O(n)에 찾아내는 알고리즘

Array의 크기 ≤ 25인 경우에는 그냥 SORT해서 selection

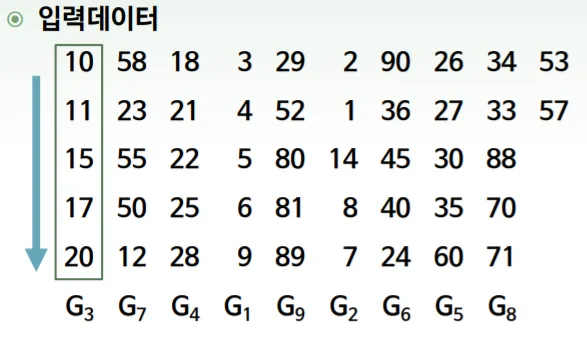
Array의 크기 > 25인 경우에는 size가 5인 subarray들로 분할한다 (n/5개)

각 subarray의 중간값(median)을 찾는다. 이들을 M배열에 저장한다고 하겠다. : 다른 SORT 알고리즘 사용 가능

M의 median을 찾아내 pivot으로 선정하고

pivot 선정 이후 quick select 알고리즘으로 k번째 원소를 반환한다.

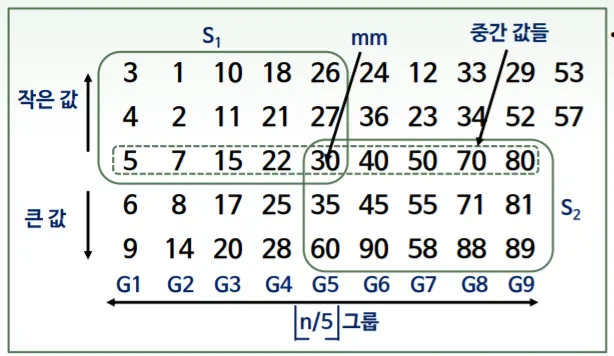
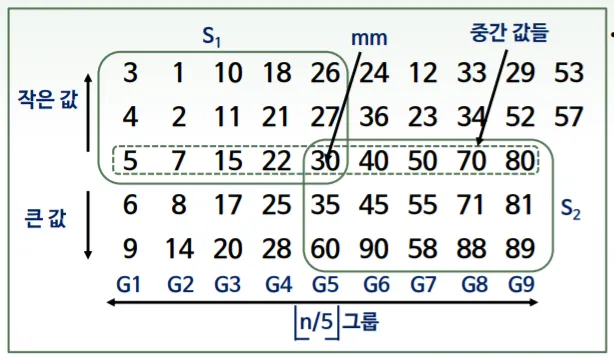
위 그림에서, 일단 subarray들은 당연히 정렬된 상태이고, 중간값들 순서에 맞추어 subarray들이 정렬되어있다고 할 때,

S1그룹 : mm보다 무조건 작음

S2그룹 : mm보다 무조건 큼

input Array의 size 인 n으로 생각하면

S1과 S2는 둘다 3n/10의 크기를 갖는다. (

3\times \frac{n}{5} \times \frac{1}{2}

)

따라서 Quick Select 매 순환마다 3n/10만큼의 원소를 배제하게 되는 것이다. 즉 subproblem의 크기가 원래 input - S1혹은 S2의 크기가 되어 subproblem은 최대 n-3n/10 = 7n/10이 된다.

pseudo 코드

int SELECT (int A[], int i, int n){
	[단계 1] if n<=5 return 배열 A에서 i번째 큰 원소
					 else 단계2~단계6 실행
	[단계 2] 배열 A를 5개의 원소로 구성된 n/5개의 그룹으로 나누고 남은 원소는 무시
	[단계 3] n/5개 그룹에서 각각 중간 값을 찾아 이를 M={m1, m2, ..., m_n/5}라 함
	[단계 4] p=SELECT(M, [n/5/2], [n/5]) -> mm을 찾음
	[단계 5] p를 분할원소 pivot으로 하여 배열 A분할. 분할 후 p가 A[j]에 놓였다고 가정
	[단계 6] while(1){
					 if i==j+1 return p
					 else if i<j+1 SELECT(A[0~j-1], i, j)
					 else SELECT(A[j+1~n-1], i-j-1, n-j-1)
					 }
C
복사

size n의 array중 k번째 작은 element를 찾는데 worst-case에도 O(n)의 시간밖에 걸리지 않는다라고 생각할 수 있지만, 실제 성능은 매우 느리다.

n/5개의 배열을 sort하고, input size가 25개 이하일 때 sort하는 과정을 상수 시간 처리했지만 이 상수 시간이 실험적으로는 매우매우 크기 때문이

하지만 이론적으로는 QuickSelect를 median of medians을 이용해서 pivot을 선정했을 때 worst-case O(n)에 구현 가능하기 때문에 굉장히 중요한 알고리즘이다.