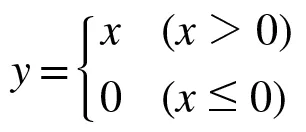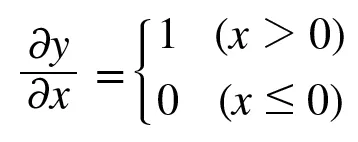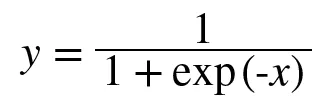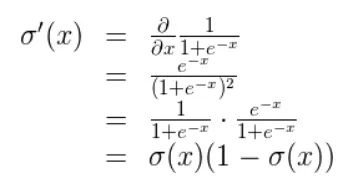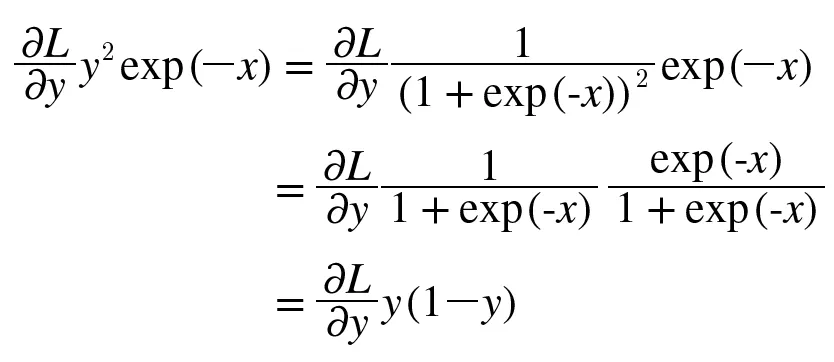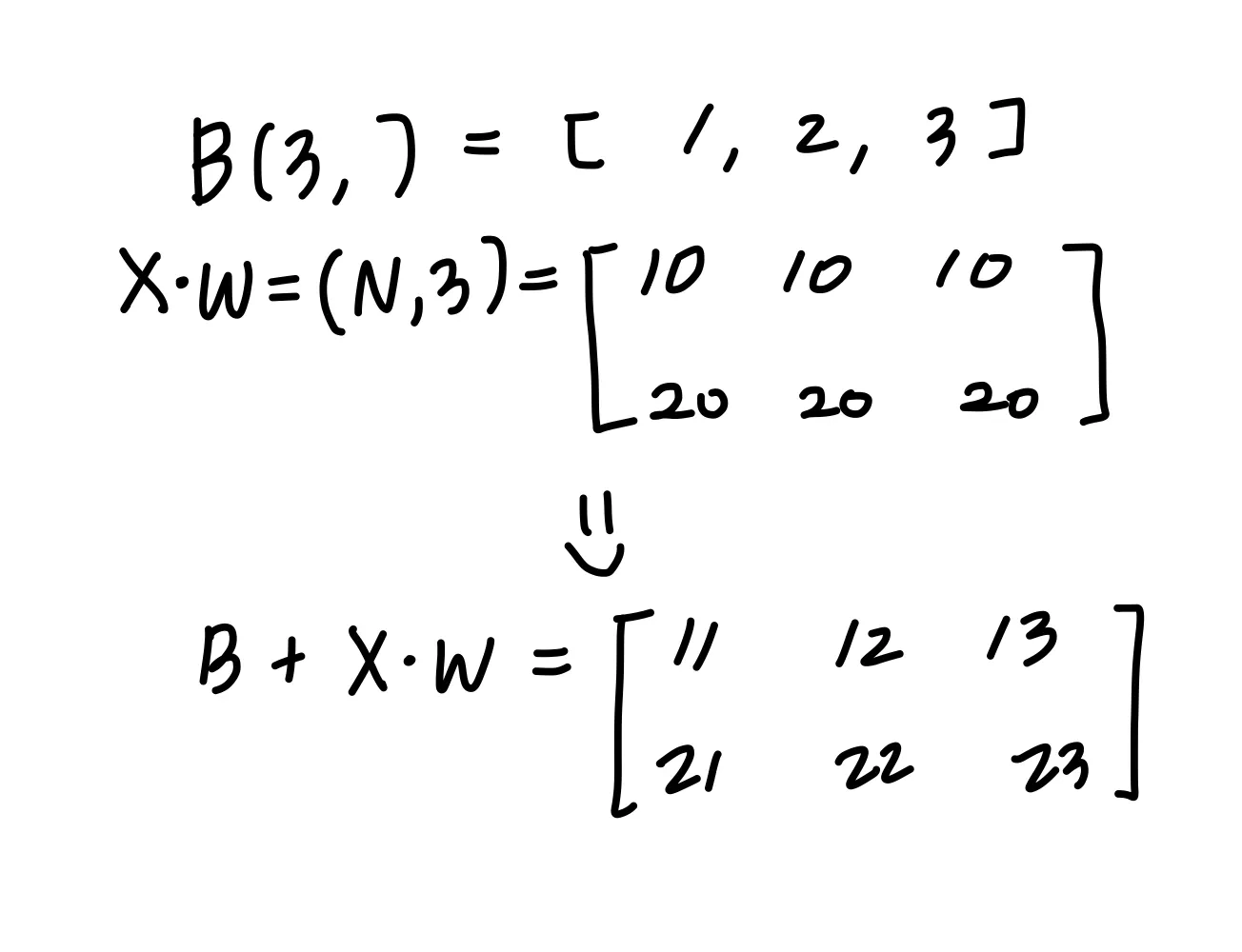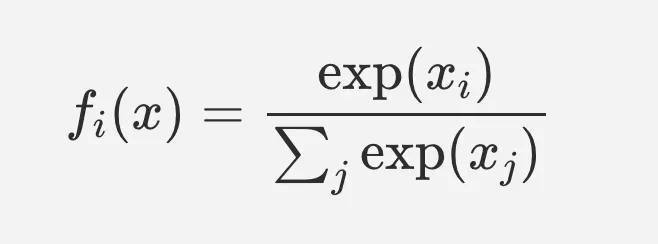Search

Classification task에서 MSE보다 Cross Entropy 를 주로 사용하는 이유?

한마디로 정리하면 “backpropagation 과정에서 이점이 있기 때문”입니다.

이를 이해하기 위해 다양한 레이어들의 역전파 과정을 살펴보겠습니다
<CNN model training 과정 ( 아주아주아주 생략 간단하게 )>
conv layer → activation function → loss function → 미분, backpropagation→gradient descent weights update

Backpropagation에서 꼭 기억하고 가야할 Chain Rule

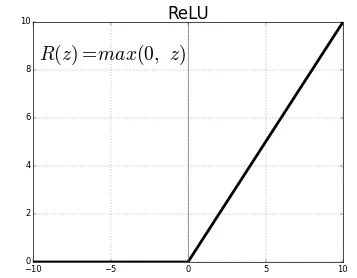
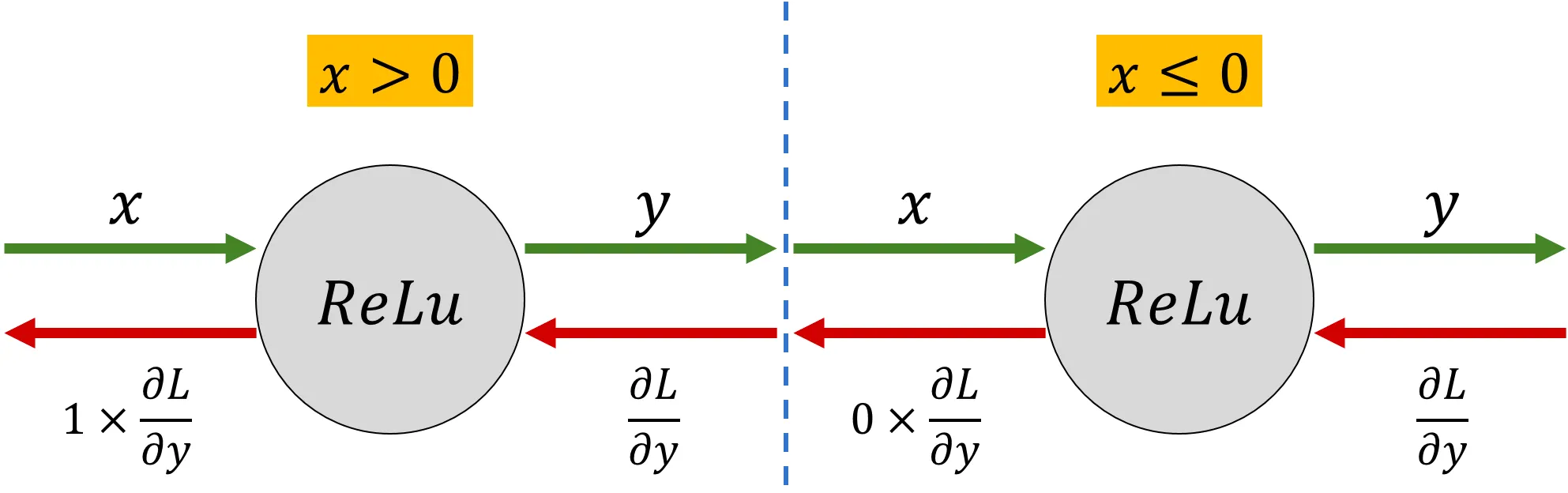
f(g(x))′=∂f∂x=∂f∂g∙∂g∂xf(g(x))^\prime =\frac{\partial f}{\partial x} = \frac{\partial f}{\partial g} \bullet \frac{\partial g}{\partial x}

ReLU

미분하면
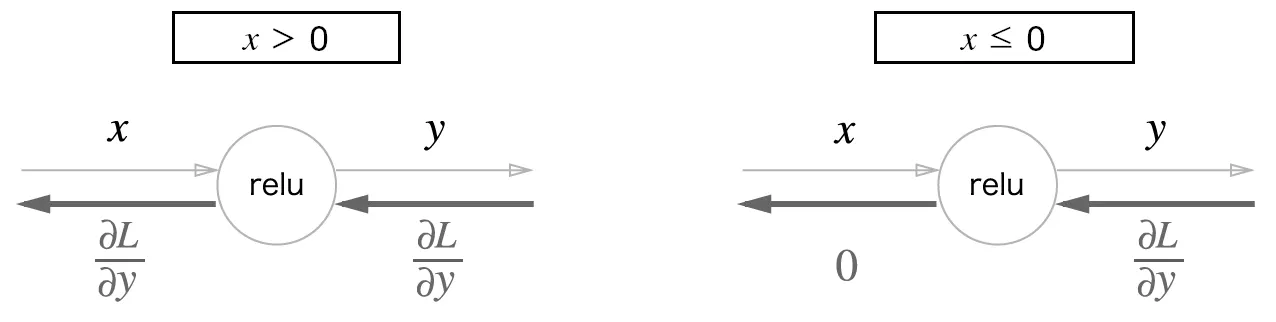
forward propagation 시, 입력인 x가 0보다 크다면 backpropagation 때에는 상류의 값을 그대로 하류로 보낸다.
입력인 x가 0보다 작다면 backpropagation 때에는 하류로 0을 보내게 된다 ( chain rule 의해 gradient가 0이 될 것이다 )

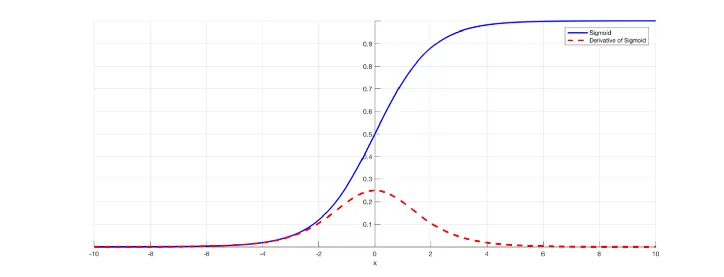
Sigmoid

파란색이 sigmoid 함수 그래프, 빨간색이 sigmoid를 미분한 것의 그래프이다.
미분식. 이해할 필요는 없다. 미분값이 0.3보다 작은 값이 나온다는 것만 알아두자

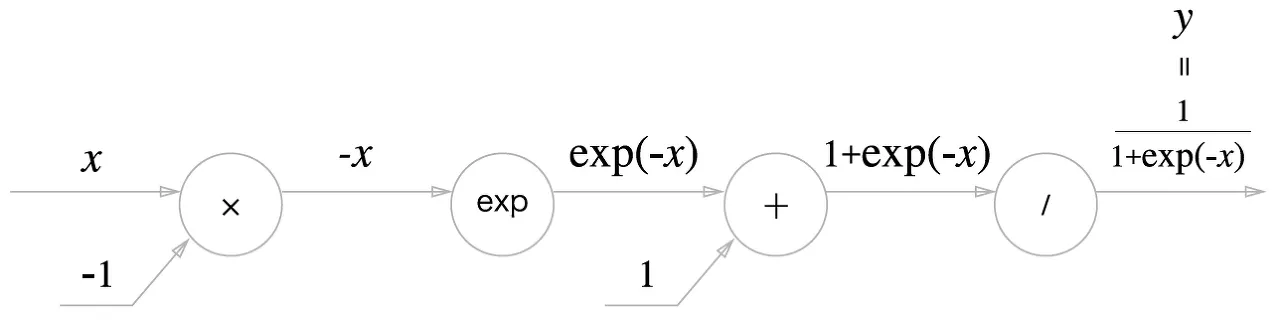
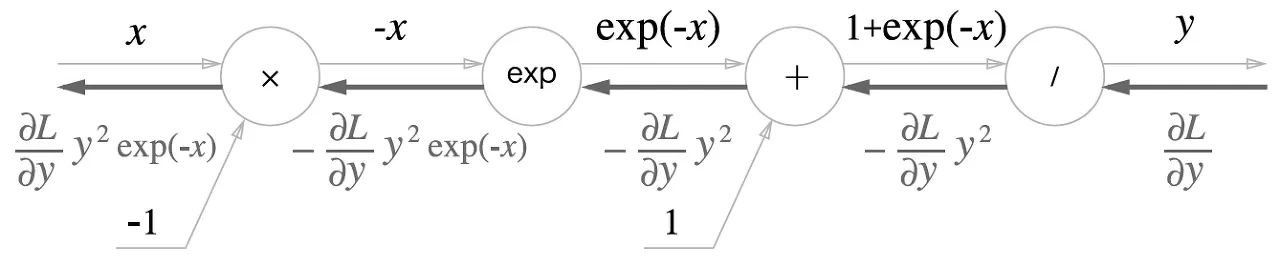
sigmoid를 계산그래프로 표현

•
×\times, exp⁡\exp , ++ , // 노드로 이뤄져 있다.
•
sigmoid의 계산은 국소적 계산의 전파라는 것을 알 수 있다.
•
forward propagation : ×→\times →exp⁡→+→/ \exp → + → / 순서로 이뤄짐
•
backpropagation : /→+→exp⁡→×/ → + → \exp → \times 순서
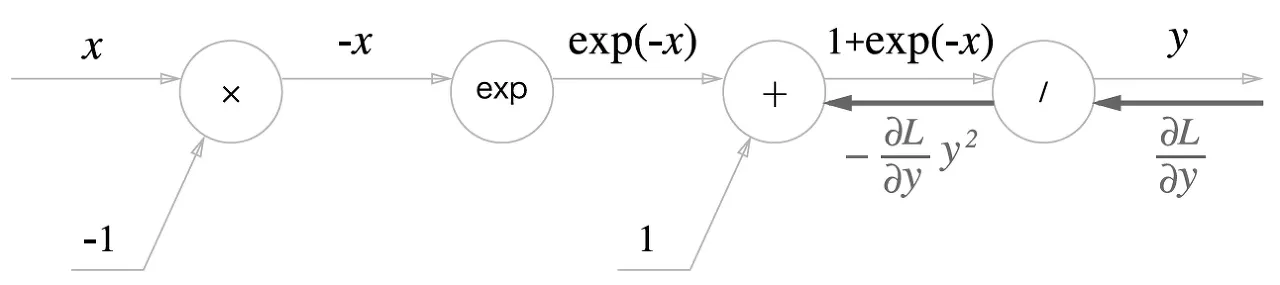
[backpropagation]
1.
// 노드
식으로 나타내면 y=1xy = \frac{1}{x}
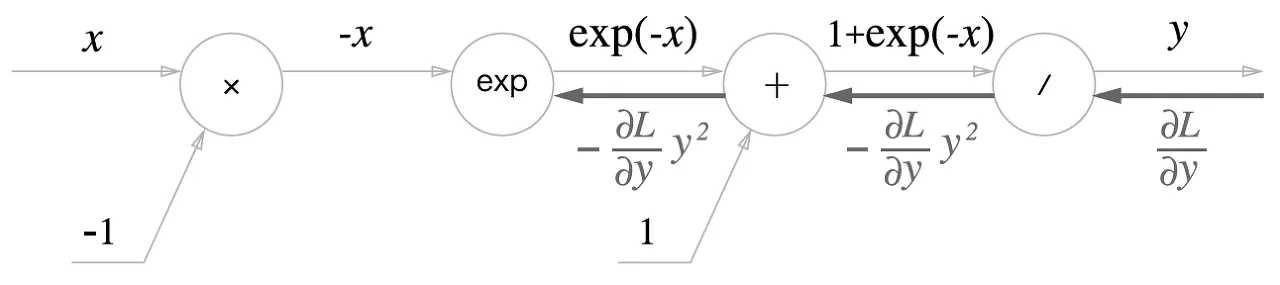
∂y∂x=−1x2=−y2\frac{\partial y}{\partial x} = -\frac{1}{x^2}=-y^2
2.
++ 노드
y=x+1y = x + 1
∂y∂x=1\frac {\partial y} {\partial x} = 1
3.
exp⁡\exp 노드
식으로 나타내면 y=exp⁡(x)=exy=\exp(x)=e^x
∂y∂x=exp⁡(x)\frac{\partial y}{\partial x} = \exp(x)
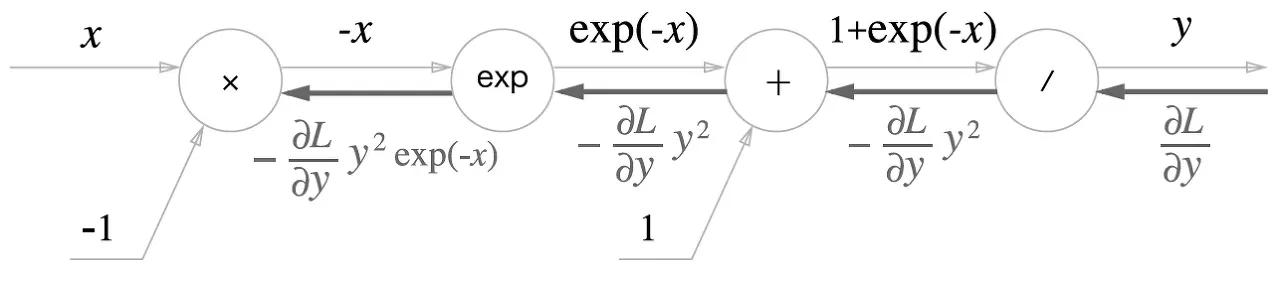
4.
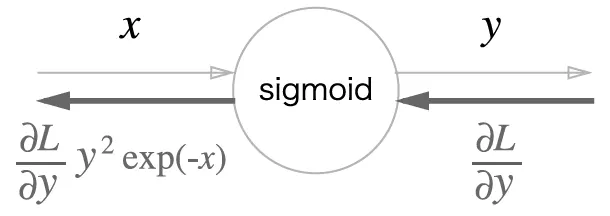
×\times 노드
y=−xy = -x
∂y∂x=−1\frac {\partial y} {\partial x} = -1
최종
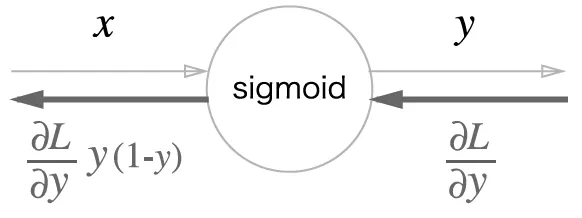
보면 결국 sigmoid의 backpropagation은 forward propagation의 출력인 y만으로 계산할 수 있다.
그래서 forward propagation의 출력을 저장했다가 backpropagation 때 사용하는 식으로 구현할 수 있다.

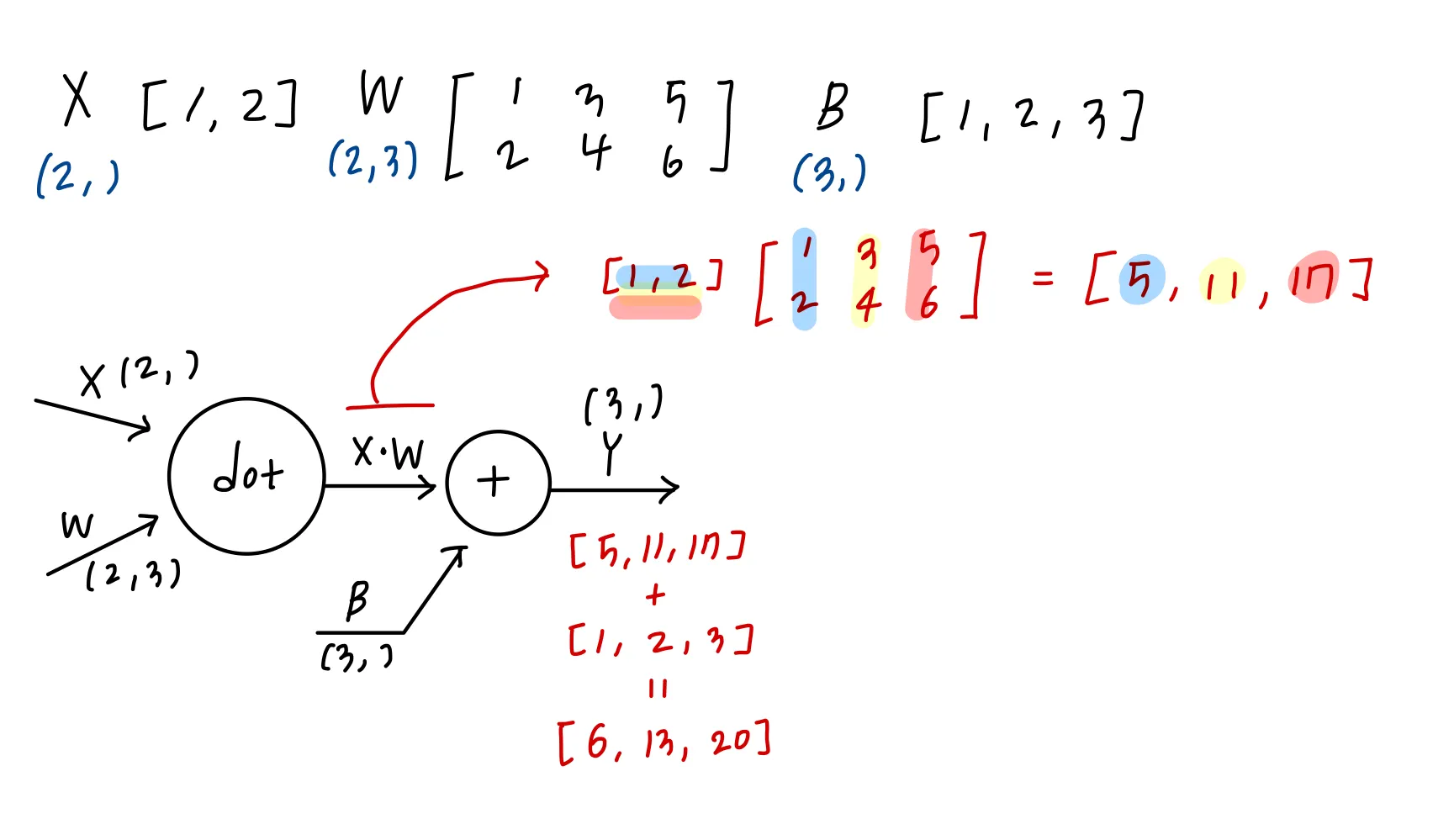
Affine 계층

neural network의 forward propagation에서의 행렬의 곱(Dot product, np.dot) : 기하학에서의 affine transformation
따라서 affine transformation을 수행하는 레이어들을 affine 계층이라고 정의
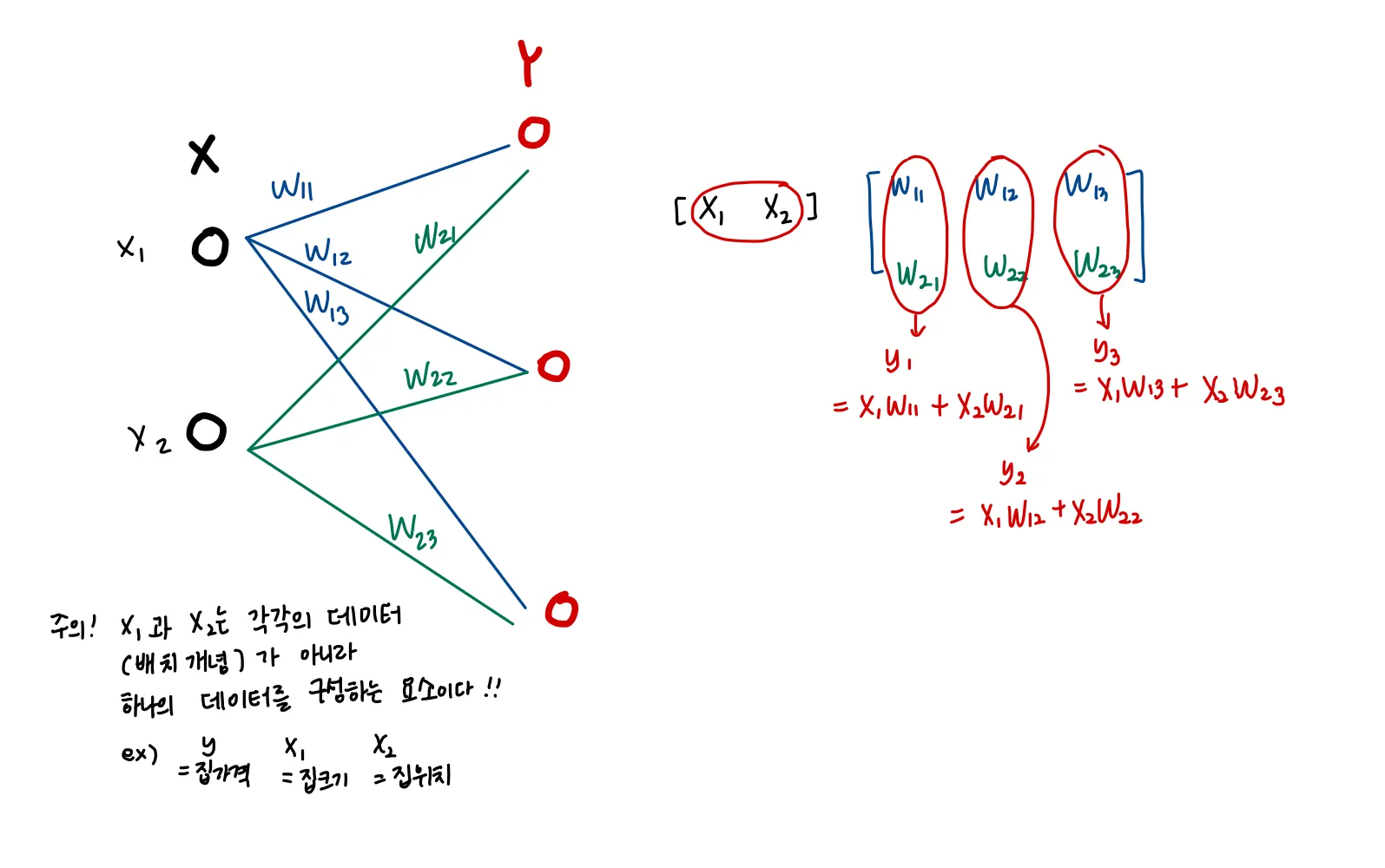
이런 계층이 무슨 계층일까? 생각해보고 FC레이어라고 생각해봤다(bias는 그리지 않았다)
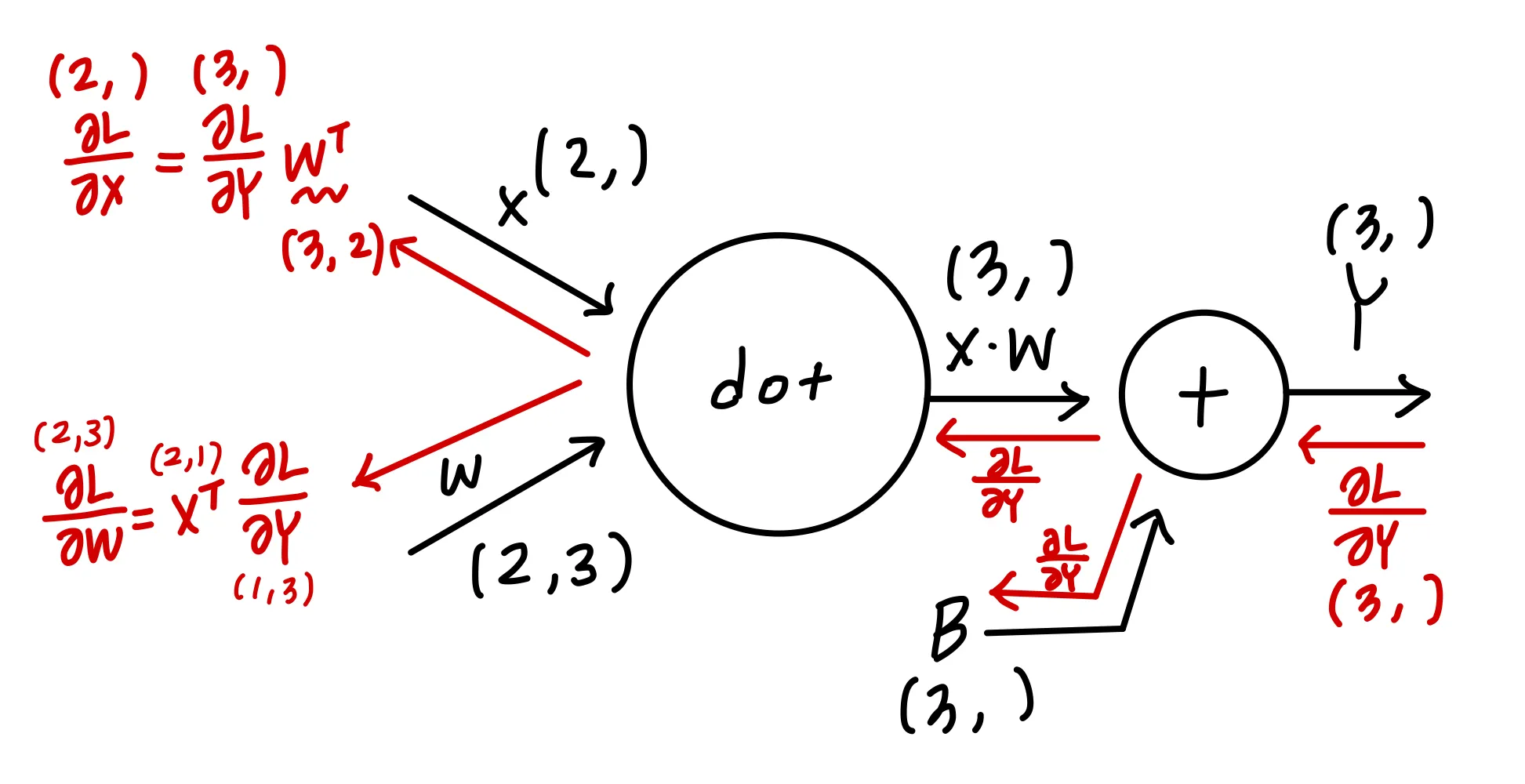
backpropagation
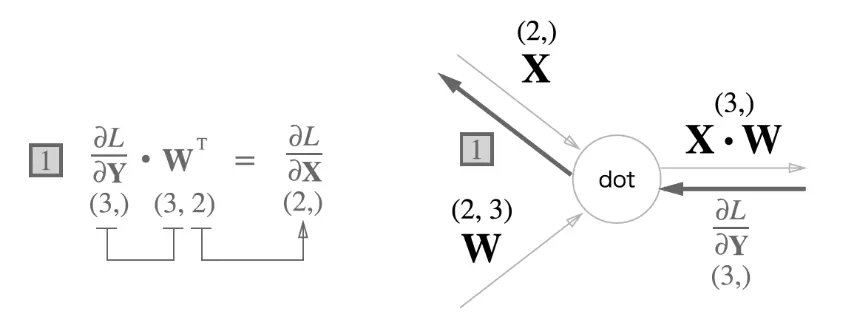
∂L∂X\frac{\partial L}{\partial X} 부분을 좀 더 보면,
다음과 같이 이뤄져있다고 볼 수 있고, 역전파시에 행렬의 대응하는 차원 원소수가 일치하도록 WTW^T 로 맞춰준다

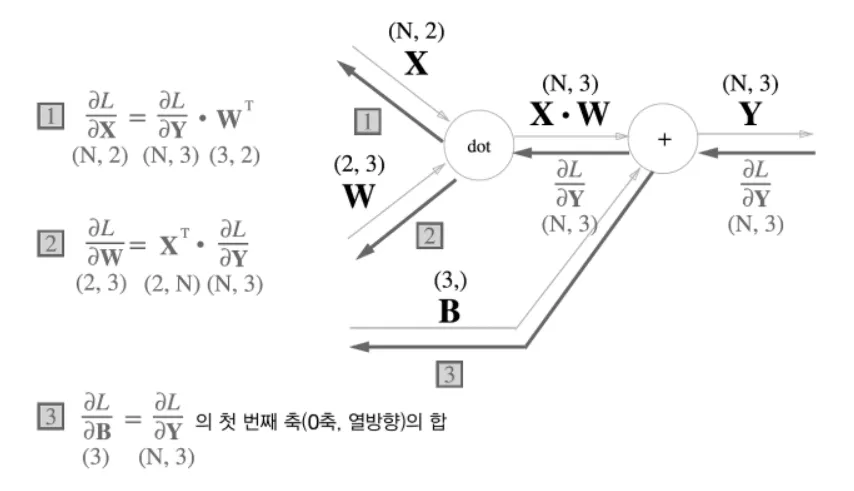
Batch를 고려한 Affine 계층

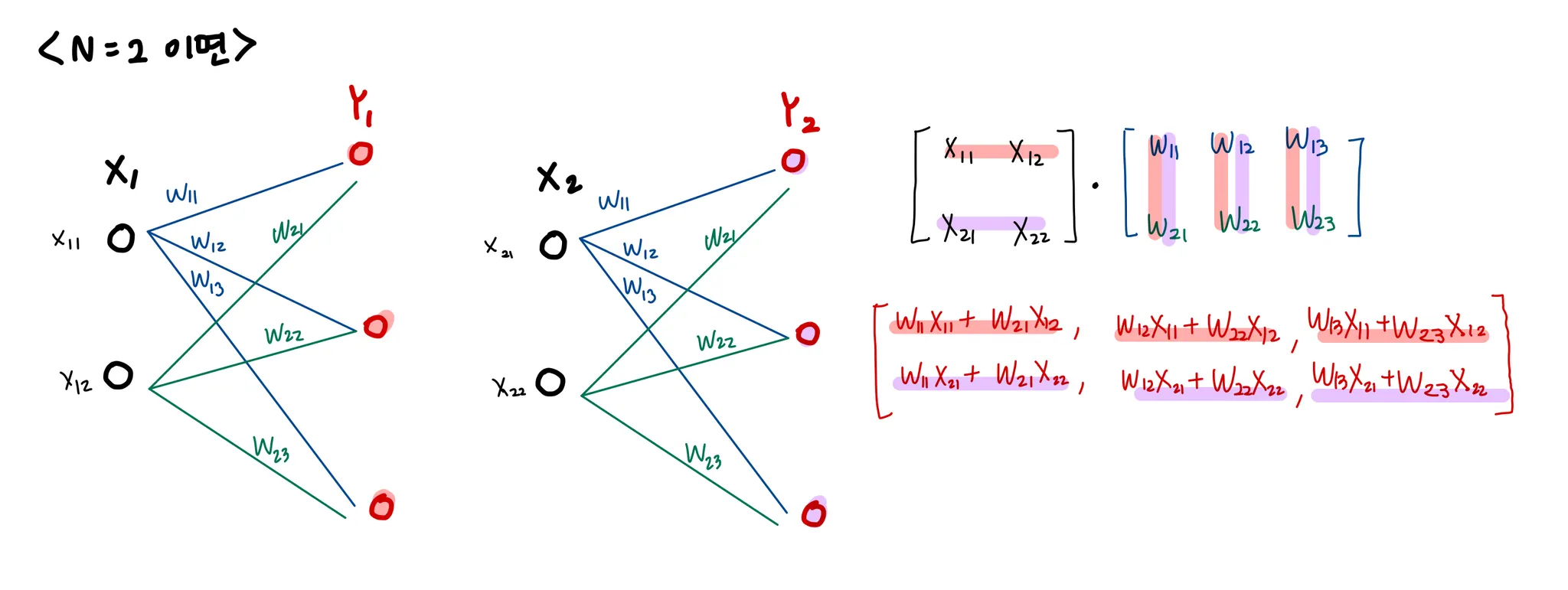
똑같이 FC 레이어로 표현하면 (bias 제외)
(3, )이었던 X가 (N, 2) 이 됐다!
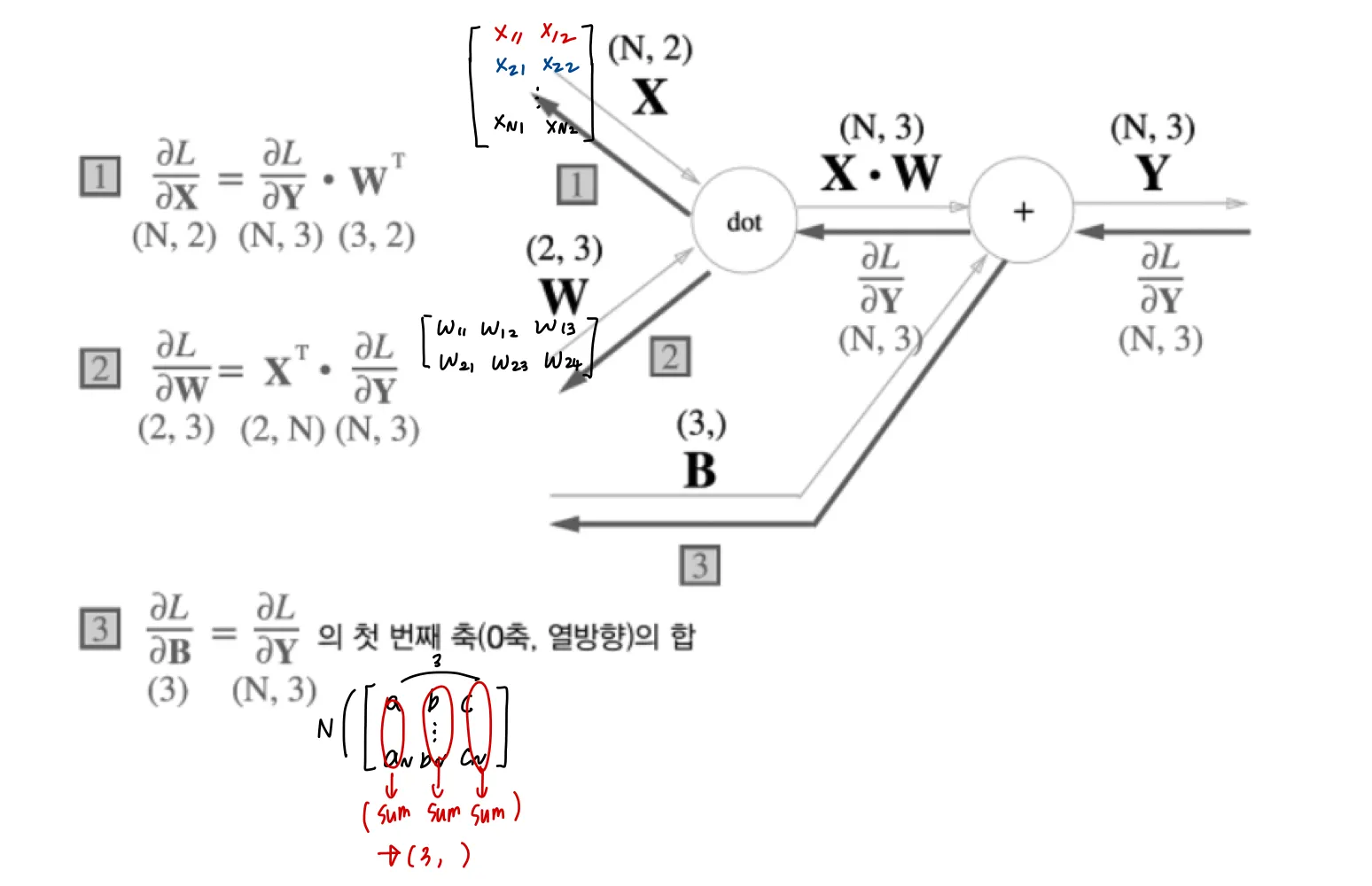
bias를 더할시에 주의해야한다.
bias 는 다음과 같이 forward propagation 시에 데이터 각각에 더해지게된다.
따라서 backpropagation bias각 데이터 ( 1, 2, 3) 각각의 역전파 값이 bias 원소에 모여야하기 떄문에, 두 데이터에 대한 미분이 데이터별로 더해지는 것이다

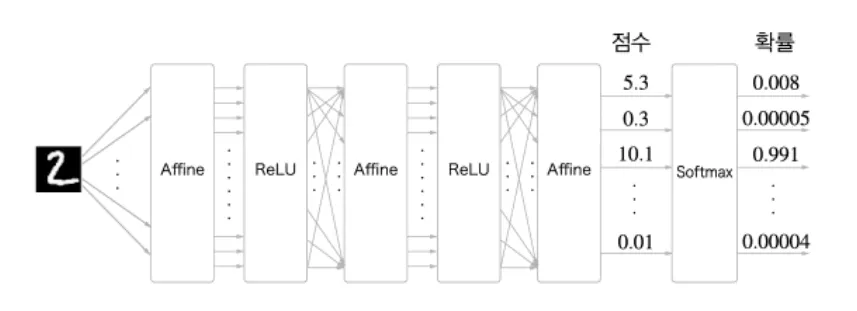
Softmax

softmax는 한마디로 입력값을 출력의 합이 1이 되도록 정규화 하여 출력한다. MNIST의 경우 10가지의 class가 있으므로 softmax계층의 입력도 10개가 된다.
NN은 학습과 추론 두 파트로 크게 나눌 수 있는데, 추론(inference)시에는 일반적으로 softmax 없이 마지막 affine 계층의 출력(score)을 인식결과로 사용한다. - 가장 높은 점수만 알면 되기 때문
학습시에는 softmax 계층이 필요하다
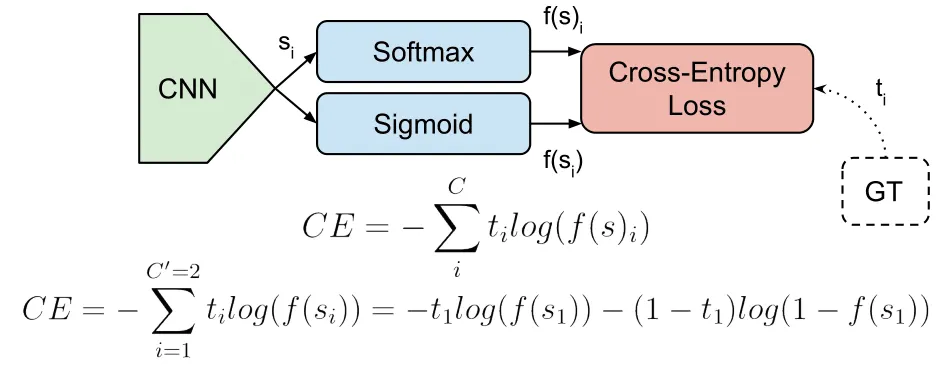
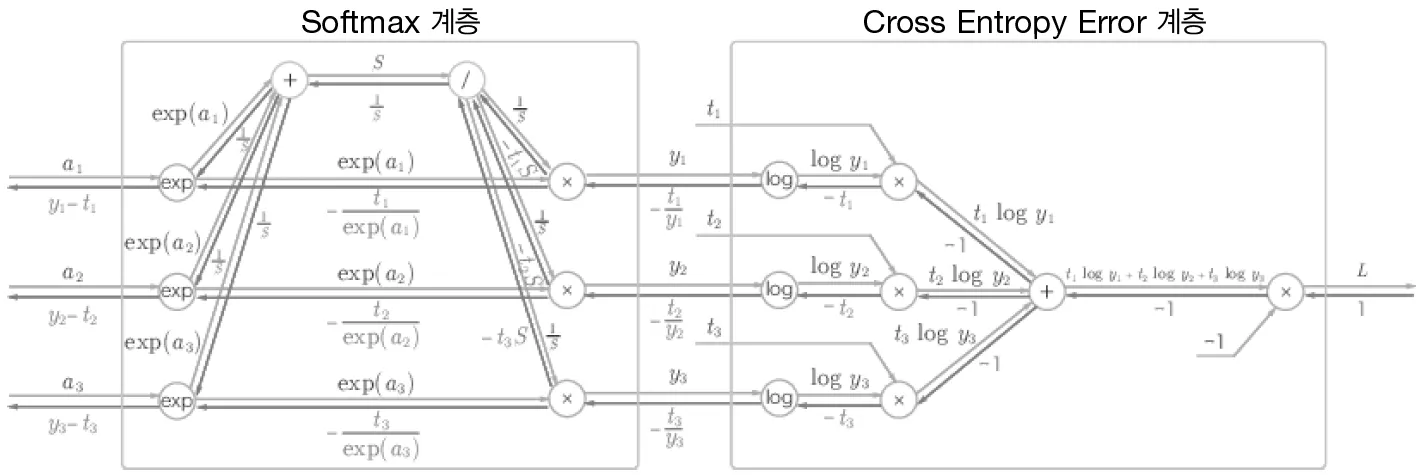
cross-entropy 까지 포함해 Softmax - CrossEntorpy 계층의 backpropagation을 살펴보자
3개 클래스 분류의 경우이다.
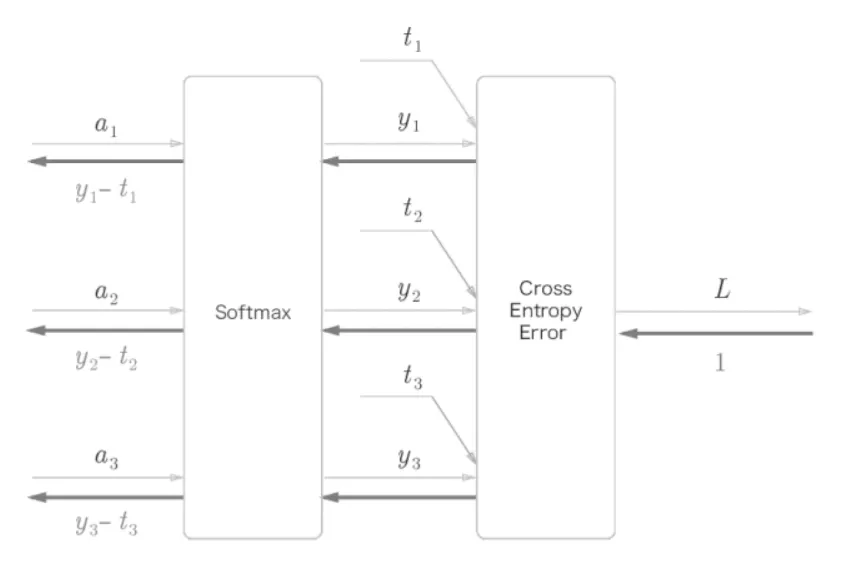
간소화하면
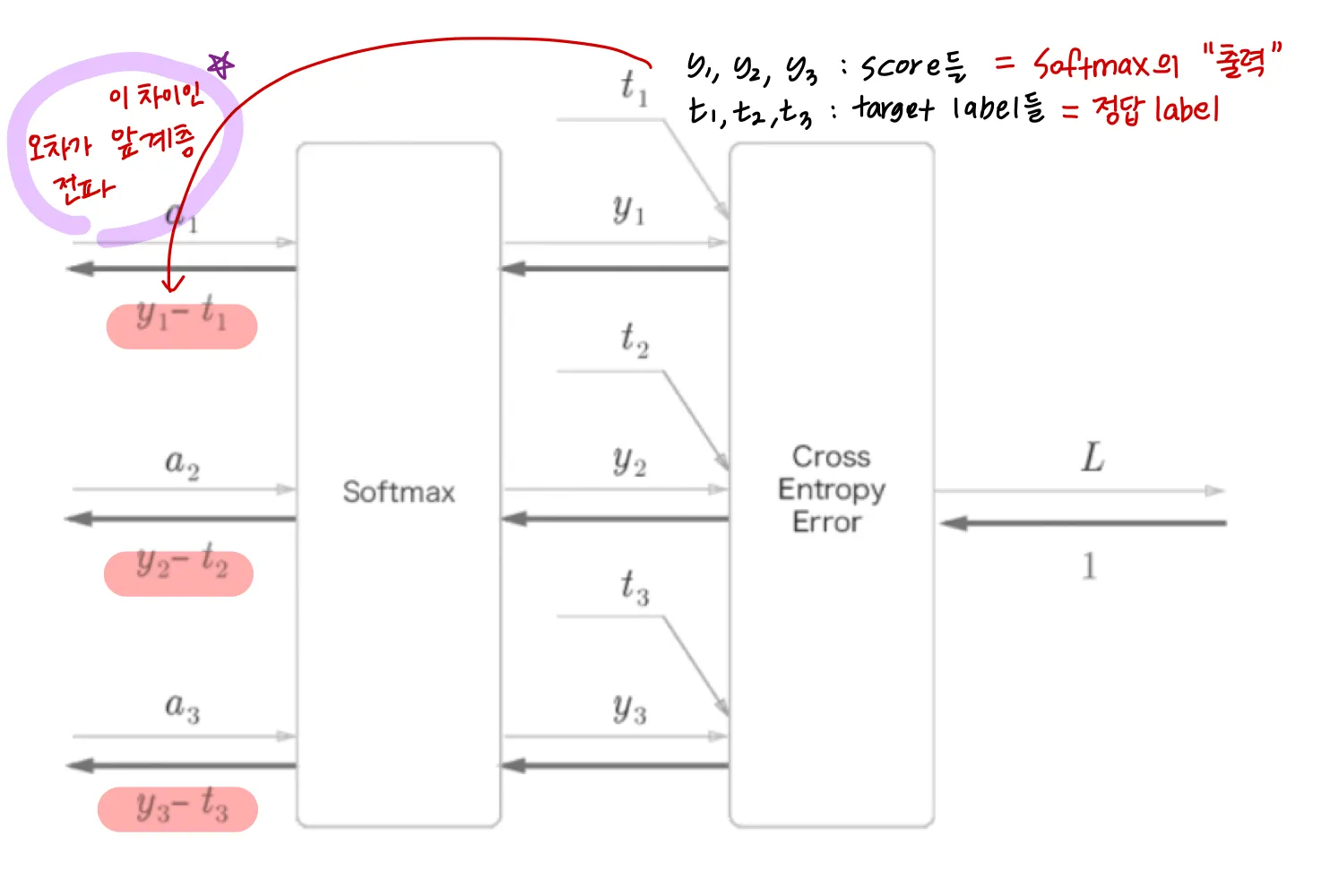
softmax에 cross entropy loss를 사용하니 back propagation 이 y1-t1, y2-t2, y3-t3으로 깔끔하게 나온다
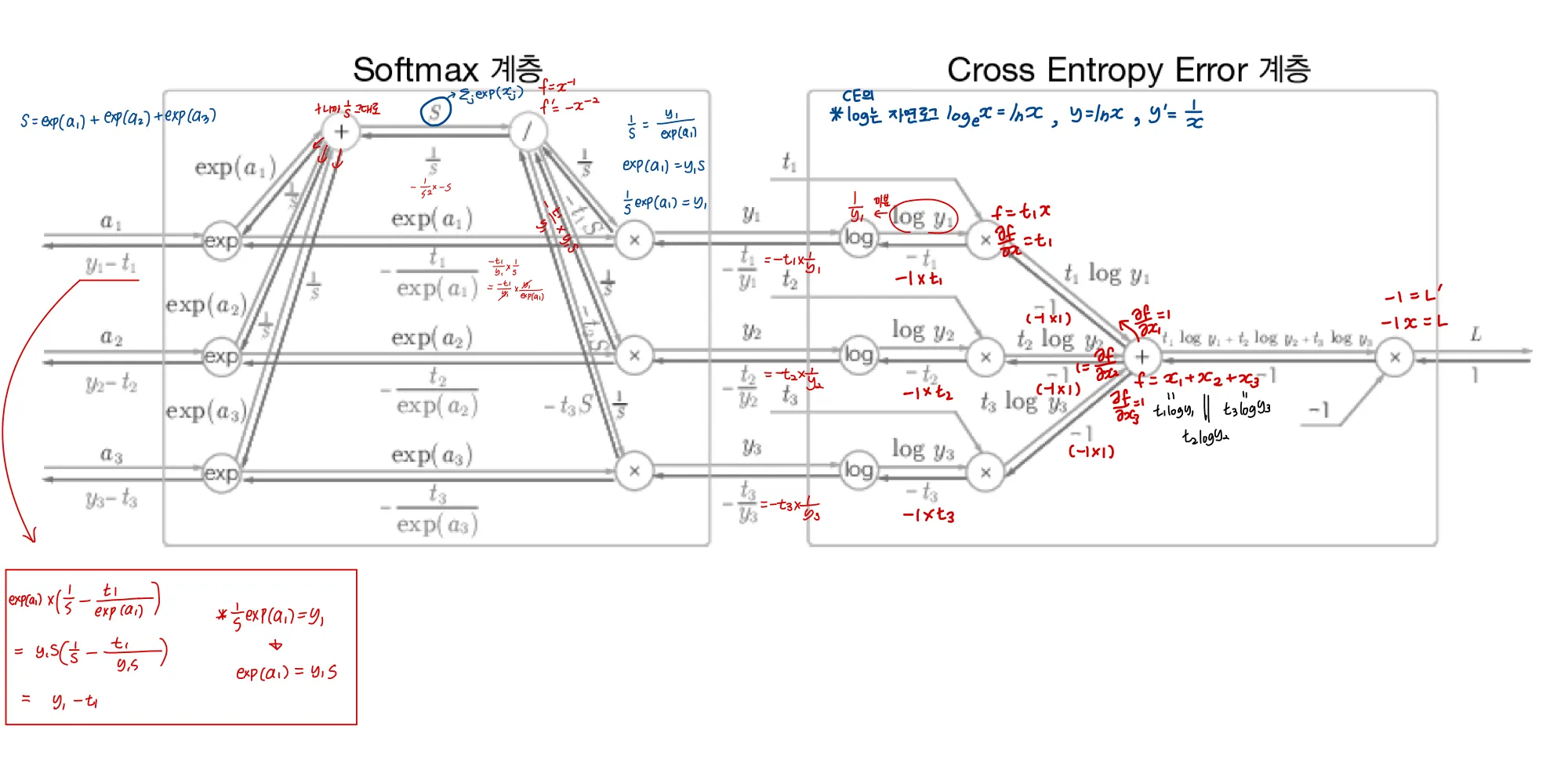
[더 자세히]
softmax-celoss-backprop-detail.pdf
232.8KB
pdf로 보면 더 잘 볼 수 있습니다!글씨가 작아서...
Made with