그래프란?
[개념]
•
단순히 노드(N, node)와 그 노드를 연결하는 간선(E, edge)을 하나로 모아 놓은 자료 구조
•
연결되어 있는 객체 간의 관계를 표현할 수 있는 자료 구조이다.
Ex) 지도, 지하철 노선도의 최단 경로, 전기 회로의 소자들, 도로(교차점과 일방 통행길), 선수 과목 등
그래프는 여러 개의 고립된 부분 그래프(Isolated Subgraphs)로 구성될 수 있다.
[특징]
•
네트워크 모델이다
•
2개 이상의 경로가 가능하다(노드들 사이에 무방향/방향에서 양방향 경로를 가질 수 있다.
•
self-loop뿐 아니라 loop, circuit 모두 가능하다.
•
root node X
•
부모-자식 관계 X
•
순회는 DFS / BFS로 이뤄짐
•
Cyclic하거나 Acyclic하다고 크게 나눌 수 있다.
•
크게 방향그래프/무방향그래프로 나눌 수 있다 - 무방향 그래프는 노드간 양방향 이동이 가능하므로 양방향 그래프로도 불린다
•
간선의 유무는 그래프에 따라 다름
[용어]
•
정점(vertex): 위치라는 개념. (node 라고도 부름)
•
간선(edge): 위치 간의 관계. 즉, 노드를 연결하는 선 (link, branch 라고도 부름)
•
인접 정점(adjacent vertex): 간선에 의 해 직접 연결된 정점
•
정점의 차수(degree): 무방향 그래프에서 하나의 정점에 인접한 정점의 수
•
무방향 그래프에 존재하는 정점의 모든 차수의 합 = 그래프의 간선 수의 2배
•
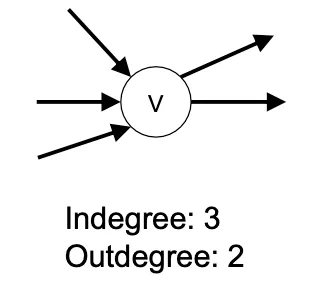
진입 차수(in-degree): 방향 그래프에서 외부에서 오는 간선의 수 (내차수 라고도 부름)
•
진출 차수(out-degree): 방향 그래픙에서 외부로 향하는 간선의 수 (외차수 라고도 부름)
•
방향 그래프에 있는 정점의 진입 차수 또는 진출 차수의 합 = 방향 그래프의 간선의 수(내차수 + 외차수)
•
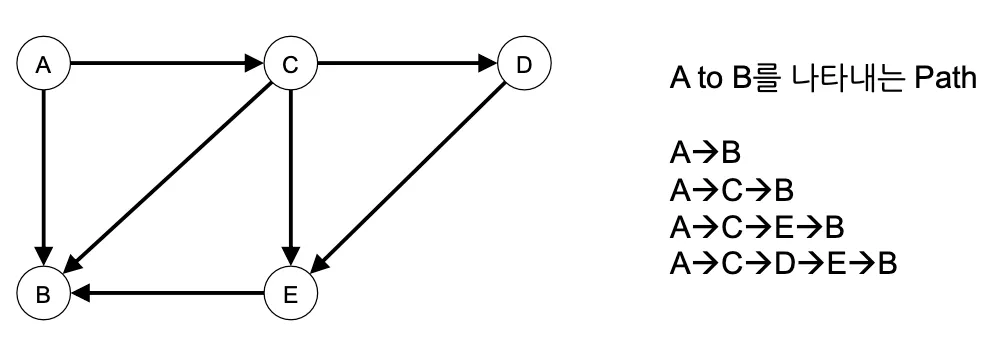
경로 길이(path length): 경로를 구성하는 데 사용된 간선의 수
•
단순 경로(simple path): 경로 중에서 반복되는 정점이 없는 경우
•
사이클(cycle): 단순 경로의 시작 정점과 종료 정점이 동일한 경우
[종류]
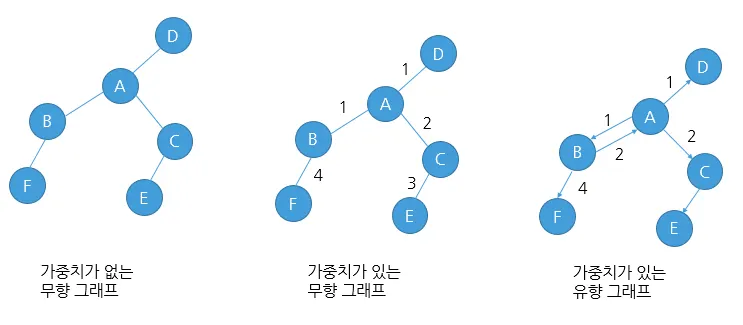
무방향그래프(Undirected Graph)
•
무방향 그래프의 간선은 간선을 통해 양 방향으로 갈 수 있다
•
정점 A와 정점 B를 연결하는 간선은 (A, B)과 같이 정점의 쌍으로 표현한다
•
(A, B)와 (B, A)는 동일하다
ex) 양방향 통행도로
방향그래프(Directed Graph)
•
간선에 방향성이 존재하는 그래프
•
A→B로만 갈 수 있는 간선 <A, B>로 표시
•
<A, B>와 <B, A>는 다르다
ex) 일방통행 도로
그외
가중치그래프(Weighted Graph)
•
간선에 비용이나 가중치가 할당
•
네트워크라고도 함
ex) 도시-도시 연결, 도로 길이, 회로 소자의 용량, 통신망 사용료
연결그래프(Connected Graph)
•
무방향 그래프에 있는 모든 정점쌍에 대해 항상 경로가 존재
ex) 트리 : cycle을 갖지 않는 연결그래프
비연결그래프(Disconnected Graph)
•
무방향그래프에서 특정 정점쌍 사이에 경로가 존재하지 않는 경우
사이클그래프(Cycle Graph)
•
단순 경로의 시작 정점과 종료 정점이 동일한 경우
•
단순경로? (Simple path) : 경로 중 반복되는 정점이 없는 경우의 경로
비순환그래프(Acyclic Graph)
•
사이클이 없는 그래프
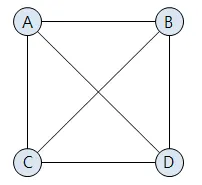
완전그래프(Complete Graph)
•
그래프에 속해있는 모든 정점이 서로 연결되어 있는 그래프
•
무방향 완전 그래프라면 정점수가 n이면 간선 수는
그래프 구현하기
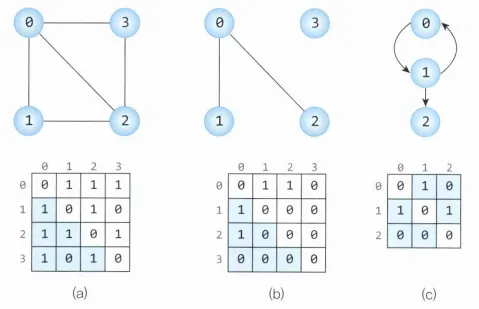
인접행렬 혹은 인접 리스트(C언어의 Linked List)형태로 표현 가능하다.
인접 행렬
정점이 n개라면 n x n 형태의 2차원 배열이 인접행렬로 사용된다.
행과 열은 정점을 의미하게 되고 각각의 원소들은 정점간의 간선을 나타낸다.
무방향그래프의 경우 인접행렬이 대칭적 구조를 갖게된다→ (a), (b)
가중치그래프의 경우 0과 1이 아닌 간선의 가중치 값이 원소로 저장된다. ( 가중치가 0인 것과 간선이 없는 것이 구별되어야 한다. )
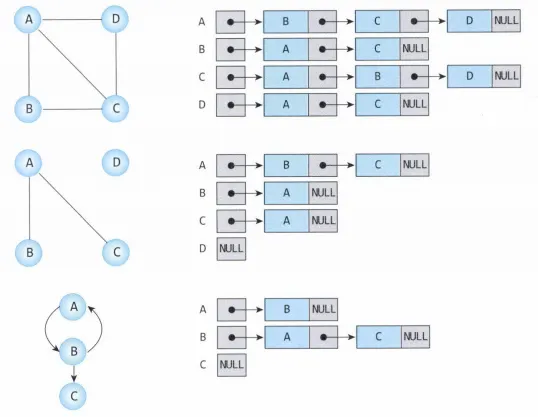
Linked List
각 정점에 인접한 정점들을 Linked List로 표현 가능하다. 좀더 직접적으로 구현하는 방법이 아닐까 싶다
따라서 그림에 보이는 것 처럼 정점의 개수만큼 linked list가 존재한다. 맨 위 그림을 보면 A에서 출발하는 linked list는 B→C→D로 연결되어있다. 모두 A와 인접한 정점들이다. 각 정점들에 대해 모두 리스트가 존재한다.
그래프는 각 인접 리스트에 대한 headpointer를 배열로 갖게된다.