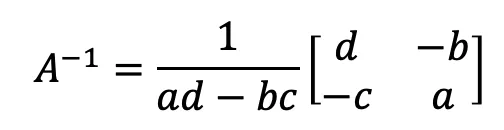Search

선형방정식/선형시스템/항등행렬/역행렬

※ 주재걸 교수님의 인공지능을 위한 선형대수 강좌를 기반으로 작성되었습니다

선형방정식(Linear Equation)

•
a1x1+a2x2+…+anxn=ba_1 x_1 + a_2 x_2 + … + a_n x_n = b
•
b와 계수(coeffients) a1,…,ana_1, …, a_n 은 real or complex numbers로 이미 아는 숫자들이다.
•
x1,…,xnx_1, …, x_n이 우리가 찾아야하는 변수들이다.
•
이 식은 다음과 같이 나타낼 수 있다
aTx=b\bold{a}^T\bold{x}=b
where a=[a1a2...an],    \bold{a} = \begin{bmatrix} a_1\\a_2\\ .\\.\\.\\a_n\end{bmatrix}, \;\; x=[x1x2...xn]\bold{x} = \begin{bmatrix} x_1\\x_2\\.\\.\\.\\x_n\end{bmatrix}

선형시스템(Linear system)

•
하나 이상의 선형방정식들의 collection
•
이 방정식들은 같은 변수들 (x1,…xnx_1, … x_n)을 포함한다.

선형시스템의 예시

personID
weight (kg)
height (ft)
is_smoking
life-span (year)
1
60
5.5
1
66
2
65
5.0
0
74
3
55
6.0
1
78
위의 데이터를 이용해 몸무게, 키, 흡연 여부를 사용해 life-span을 맞추는 선형시스템을 설계하고 싶다.
그럼 다음과 같이 세개의 식을 만들 수 있다.
60x1+5.5x2+1x3=6665x1+5.0x2+0x3=7455x1+6.0x2+1x3=7860x_1+5.5x_2+1x_3=66\\65x_1+5.0x_2+0x_3=74\\55x_1+6.0x_2+1x_3=78
x1,x2,x3x_1, x_2, x_3을 구하면 unseen data, 즉 임의의 사람의 몸무게, 키, 흡연여부를 알면 그 사람의 수명을 예측할 수 있다.
위의 연립방정식은 matrix의 곱으로 간단히 나타낼 수 있다.
A=[605.51655.00556.01]A = \begin{bmatrix} 60&5.5&1 \\ 65&5.0&0 \\ 55&6.0&1\end{bmatrix} , x=[x1x2x3]\bold{x}=\begin{bmatrix} x_1\\x_2\\x_3\end{bmatrix}, b=[667478]b=\begin{bmatrix} 66 \\ 74 \\ 78 \end{bmatrix}
Ax=bA\bold{x}=b
•
어떻게 x\bold{x}를 구할 수 있을까?
선형시스템을 푸는 방법 중 하나는 역행렬을 사용하는 것이다.

역행렬과 항등행렬

항등행렬 (Identity matrix)

항등행렬은 정방행렬(square matrix)로, 대각성분이 모두 1이고 다른 값들은 모두 0인 행렬이다. 보통 In∈Rn×nI_n \in \mathbb{R}^{n \times n}으로 표현한다.
항등행렬에 어떤 벡터 x∈R\bold{x} \in \mathbb{R}을 곱하든 x\bold{x} 를 보존한다.
∀x∈Rn,    Inx=x\forall \bold{x} \in \mathbb{R}^n, \;\; I_n\bold{x}=\bold{x}

역행렬(Inverse matrix)

정방행렬 A∈Rn×nA\in \mathbb{R}^{n \times n}에 대해서, 그것의 역행렬 A^{-1}은 다음과 같이 정의된다.
A−1A=AA−1=InA^{-1}A = AA^{-1}=I_n
•
2x2 matrix 에 대한 역행렬 구하는 공식
더 큰 차원의 행렬들에 대한 공식도 존재하고 알고리즘도 존재한다.
이걸 이용해서 어떻게 Linear System을 풀까?

Soling Linear System via Inverse matrix

Ax=bA−1Ax=A−1bInx=A−1bx=A−1bA \bold{x} = b\\ A^{-1}A \bold{x}=A^{-1}b\\I_n\bold{x}=A^{-1}b\\\bold{x}=A^{-1}b
이러한 과정을 통해 역행렬을 이용해 변수 x\bold{x}를 구할 수 있다.
위와 같이 A에 대한 역행렬을 연산한 후 b에 곱하여 x\bold{x}를 구해냈다.
이제 누군가의 life-span은 −0.4×weight+20×height−20×is_smoking-0.4 \times weight + 20 \times height - 20 \times is\_smoking 으로 구할 수 있다.

Non-Invertible matrix A for Ax=b

역행렬이 존재할 때는 해는 오직 하나가 된다. 이는 다음과 같은 예시로 확인할 수 있다.
예시)
우리가 구한 해가 x이고, x*라는 해가 또 하나 존재한다고 가정을 한다면,
Ax∗=bA\bold{x*} = \bold{b}
AA−1x∗=A−1bAA^{-1}\bold{x}*=A^{-1}\bold{b}
x∗=A−1b\bold{x*}=A^{-1}\bold{b}
결국 x=x∗\bold{x} = \bold{x}*가 된다.
그러나 역행렬이 존재하지 않으면, 해가 없거나 무수히 많게 된다.
역행렬이 존재하는지 안하는지는 보통 행렬식(determinant)을 통해 확인한다. A의 행렬식은 det A로 표기한다.
행렬식은 역행렬을 구하는 식에서 찾을 수 있다.
ex) 2차원 정방행렬의 역행렬 공식
for  A=[abcd],    A−1=1ad−bc[d−b−ca]for \; A=\begin{bmatrix} a &b \\ c&d\end{bmatrix}, \;\; A^{-1}=\frac{1}{ad-bc}\begin{bmatrix} d &-b \\ -c&a\end{bmatrix}
여기서 denominator ad−bcad-bc 가 행렬식이다.더 큰 차원의 정방행렬에 대해서도 공식이 존재한다.
보통 det A가 0인 경우 역행렬이 존재하지 않는다고 판단한다.
•
det A = 0: invertible
•
det A ≠ 0 : non-invertible
행렬식은 이 외에도 선형변환에서 초부피를 확대시키는 배수(절댓값) 및 방향 보존 여부(부호)를 뜻하기도 한다.
그럼 위의 2차원 정방행렬의 경우로 직접 확인해보자.
ex) det A = 0일 때
[1224][xy]=[36]\begin{bmatrix} 1&2\\2&4\end{bmatrix}\begin{bmatrix} x\\y\end{bmatrix}=\begin{bmatrix}3\\6\end{bmatrix}
1×4−2×2=01 \times 4 - 2 \times 2 = 0 으로 행렬식 값이 0인 상황이다. 이를 연립방정식으로 표현하면 다음과 같다.
x+2y=32x+4y=6x+2y=3\\2x+4y=6
하나의 변수를 소거하려고 해보면 2(x+2y)−(2x+4y)=(2x+4y)−(2x+4y)=0x+0y=02(x+2y) - (2x+4y) = (2x+4y) - (2x+4y) = 0x + 0y=0 로 무수한 해를 가지게 된다. 결국 둘은 같은 식인 것이다. 즉, y=−12x+32y= - \frac{1}{2}x + \frac{3}{2} 직선 위의 모든 점이 해가 된다.

Rectangular Matrix 의 경우

personID
weight (kg)
height (ft)
is_smoking
life-span (year)
1
60
5.5
1
66
2
65
5.0
0
74
3
55
6.0
1
78
지금까지는 정방행렬 A∈Rm×nA\in \mathbb{R}^{m \times n}의 경우, 즉 위와 같이 variable 수 (n)과 equation 수 (m)이 같은 경우를 확인했다. 즉, 연립방정식을 푸는데 방정식의 개수와 변수의 개수가 동일한 것이다. 중고등학교 때 배웠듯, 이 경우에 유일한 해를 찾을 수 있다.
그러나 m<n이거나 m>n인 경우는 어떨까
•
m<n : 방정식 수 < 변수 수 : 보통 무한한 해가 존재 (under-determined system)
•
m>n : 방정식 수 > 변수 수 : 보통 해가 존재하지 않음 (over-determined system)
보통의 머신러닝 task들은 m<n의 경우이다. 이를 해결하기 위해 보통 regularization을 사용한다. regularization은 간단히 말해 objective 계산시에 제약을 주어 특정 w의 값이 너무 커지는 현상을 억제한다.
위의 예시 의 경우, y=−12x+32y= - \frac{1}{2}x + \frac{3}{2} 위의 모든 점이 해가 될 수 있다고 했다. 두 점을 뽑아보자면 (1, 1)과 (5, -1)이 가능하다. xx가 몸무게에 대한 weight, yy가 키에 대한 weight라고 가정하면, regularization을 적용해 학습한 머신러닝 모델은 (1,1)을 선호한다. 왜냐하면 (5, -1)의 경우 몸무게값에 너무 의존하게 되어 overfitting이 발생할 수 있기 때문이다.
Made with