1. step function
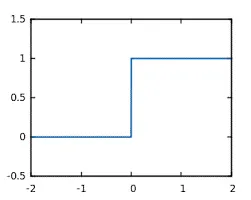
초기 퍼셉트론의 경우 step function을 활성화 함수로 사용하였는데, 어떠한 값보다 크면 1을, 아니면 0을 내보내는 함수입니다.
def step_function(x) :
if x > 0: return 1
else: return 0
def step_function(x):
y = x>0
return y.astype(np.int)
Python
복사
뉴런의 특성을 그대로 적용한 함수이다. 그러나 미분이 불가능하다는 큰 단점이 있어서 backpropagation 학습이 불가능합니다.
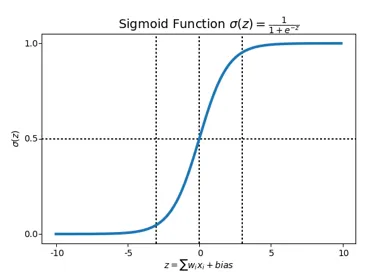
2. Sigmoid
연속적인 함수이기 때문에 모든 구간에서 미분이 가능하게 되었습니다!
def sigmoid(x):
return 1 / ( 1 + np.exp(-x))
Python
복사
sigmoid의 문제 1
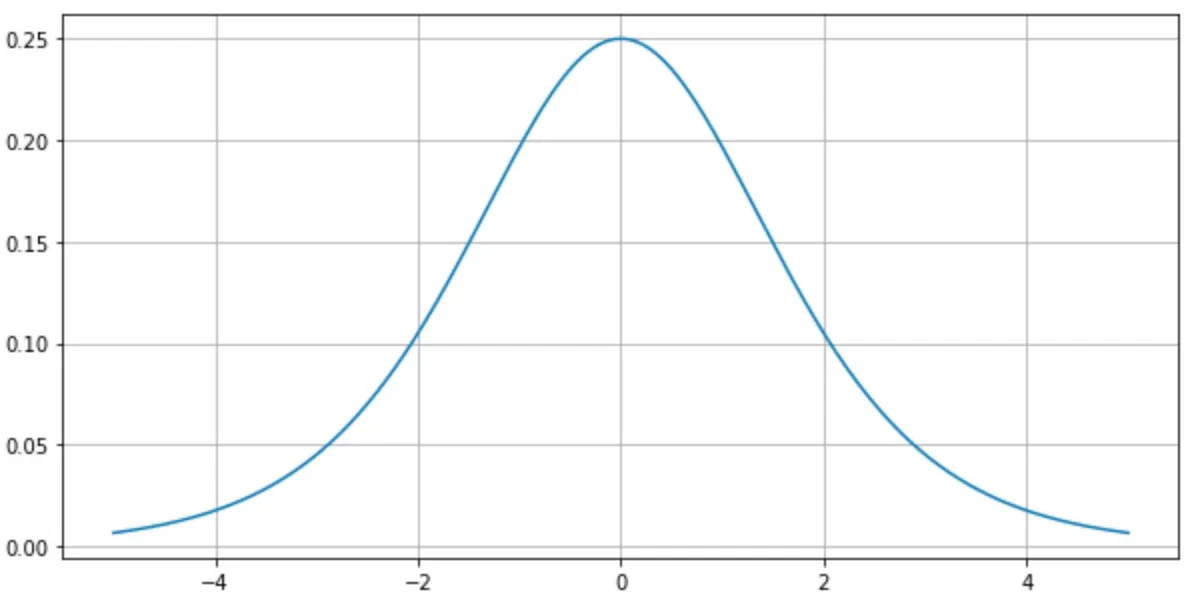
그러나 sigmoid의 미분값은
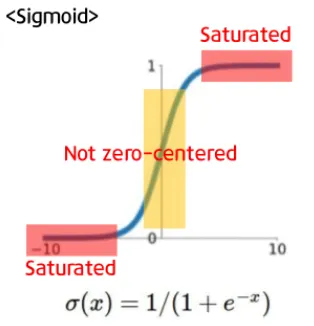
입력신호값이 크거나 작으면 기울기가 0에 가까워집니다. 이 현상을 saturated라고 합니다
이 현상은 backbropagation시 chain rule에 의해 vanishing gradient문제가 발생하게 됩니다
sigmoid의 문제 2
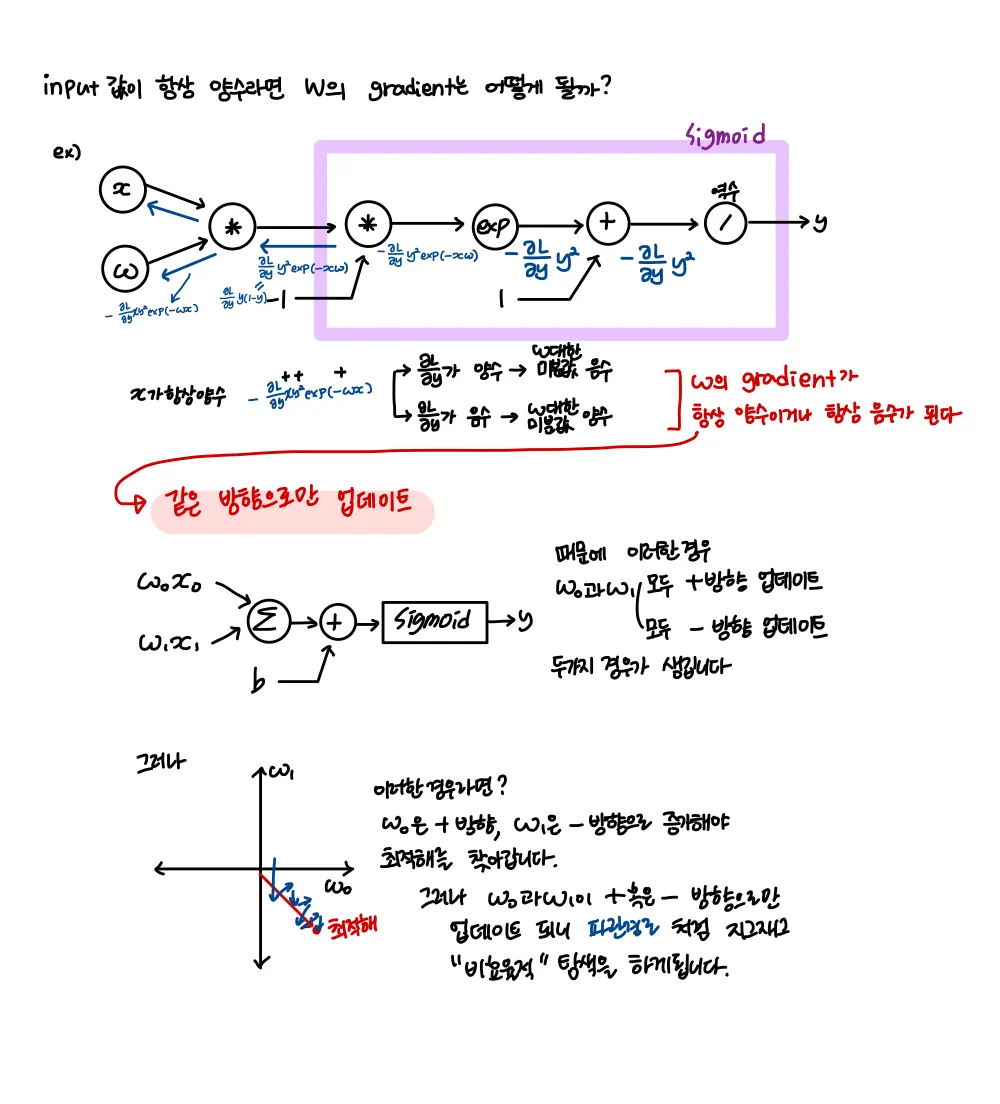
sigmoid는 zero-centered하지 않습니다.
그래서 zero mean data를 일반적으로 선호하는 것이기도 합니다 ( 입력데이터가 양수 / 음수 모두를 가짐 )
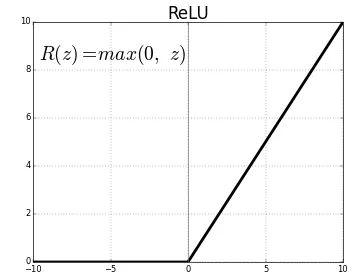
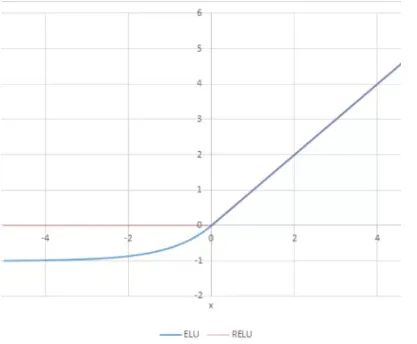
3. ReLU ( Rectifier Linear Unit = ramp function )
def relu(x):
return np.maximum(0, x)
Python
복사
이 함수는 sigmoid와 달리 출력값의 범위 제한이 없습니다.
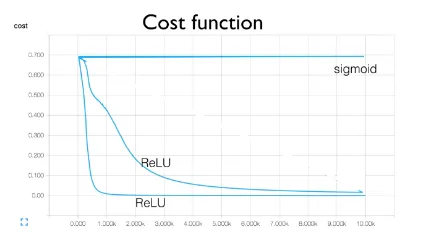
또한 0 이상이면 미분값이 1로 일정하기 때문에 backpropagation도 잘 됩니다
그러나 non-zero centered 문제는 여전히 존재합니다 또한 음수영역에서는 saturated됩니다
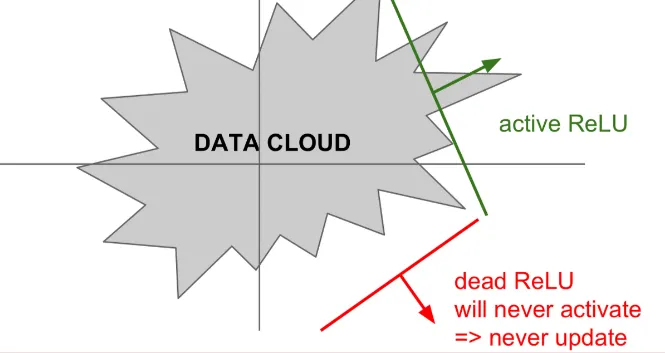
그러나 0보다 작은 값들은 그냥 0으로 버려버리기 때문에 값이 0이하인 경우의 weights는 업데이트가 이뤄지지 않습니다.
위 그림과 같이 ReLU가 data cloud에서 멀리 떨어져 있으면 Dead ReLU가 발생합니다
이러한 경우는
1.
가중치 초기화를 잘못한 경우 → 가중치 평면이 data cloud에서 멀리 떨어져있음
2.
learning rate가 높은경우 → ReLU가 데이터의 manifold를 벗어나게됨
두가지가 흔한 경우입니다.
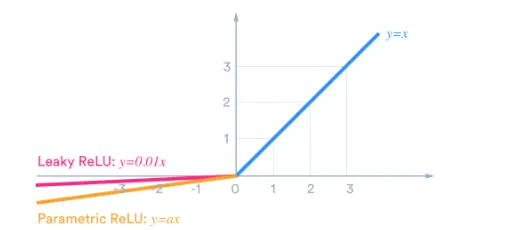
그러나 가 음수값이어도 의미있는 값일 수 있으니 반양을 조금이라도 해주면 좋지않을까요?
기타 음수값 반영 activation function
0.01이라는 값은 하이퍼파라미터로 조정이 가능합니다
학습가능한 파라미터 를 사용합니다
현재 인 경우는 그대로 x를 출력해주는 것이 보편화되었습니다.
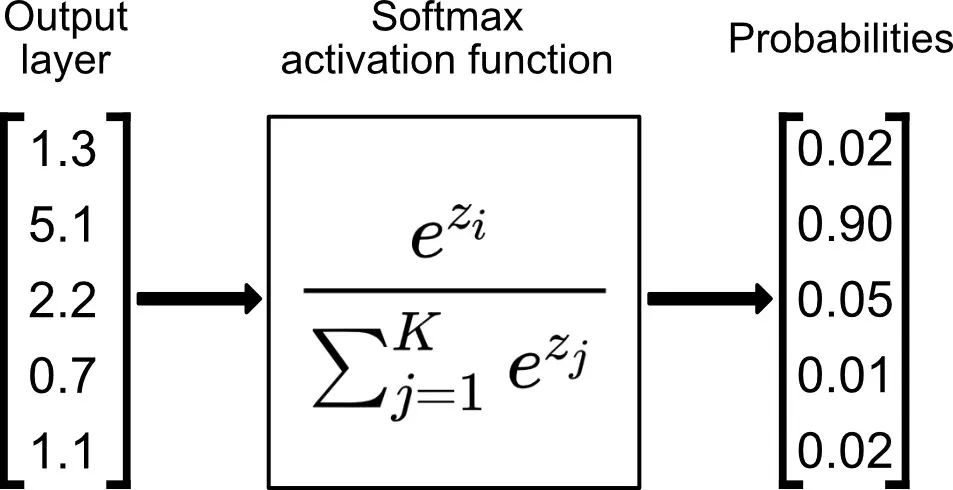
Softmax
이 함수는 보통 네트워크 마지막에 확률적 값을 얻기 위해 사용되곤합니다. ReLU나 sigmoid처럼 레이어마다 사용되는 일은 드뭅니다.
비선형 함수
이 함수들은 모두 비선형함수라는 공통점이 있습니다
다르게 말하면 신경망에서 활성화함수는 비선형 함수를 사용해야 합니다. 즉, 선형함수를 사용해선 안됩니다
왜?
선형함수를 층을 깊게 쌓아봤자 hidden layer가 없는 상황과 같다는 문제가 있습니다.
예를 들어 이고 이 레이어들을 쌓았다고 생각하면 가 되기때문에 결국엔 의 형태로 의 기능과 다를바가 없습니다
따라서 비선형 함수를 사용해 층을 깊게 쌓는 장점을 살려주어야 합니다.
⇒ activation function을 포함한 다수의 레이어를 갖는 MLP는 non-linear한 문제를 풀 수 있다 ⇒ universal approximation theorem
“ activation function 영향 아래 추가된 hidden layer는 연속함수를 근사화할 수 있고 이에 따라 적절한 가중치가 주어지면 다양한 함수들을 표현할 수 있다