빅오/정렬알고리즘, selection sort, bubble sort

빅오 표기법

연산 횟수를 대략적으로 표기한 것 - 함수의 상한을 의미

빅오표기의 성질

•

2n2−5n+7=O(n2),O(n3),O(n4),...2n^2-5n+7=O(n^2),O(n^3),O(n^4),...2n2−5n+7=O(n2),O(n3),O(n4),...

•

f1(n)=O(g1(n)),f2(n)=O(g2(n))f_1(n) = O(g_1(n)), f_2(n) = O(g_2(n))f1​(n)=O(g1​(n)),f2​(n)=O(g2​(n))일 경우

f1(n)+f2(n)=O(g1(n)+g2(n))=O(max(g1(n),g2(n)))f_1(n)+f_2(n) = O(g_1(n)+g_2(n))=O(max(g_1(n), g_2(n)))f1​(n)+f2​(n)=O(g1​(n)+g2​(n))=O(max(g1​(n),g2​(n)))

f1(n)⋅f2(n)=O(g1(n)⋅g2(n))f_1(n) \cdot  f_2(n) = O(g_1(n)\cdot g_2(n))f1​(n)⋅f2​(n)=O(g1​(n)⋅g2​(n))

O(1)<O(\log{n})<O(n)<O(n\log{n})<O(n^2)<O(n^3)<...<O(2^n)

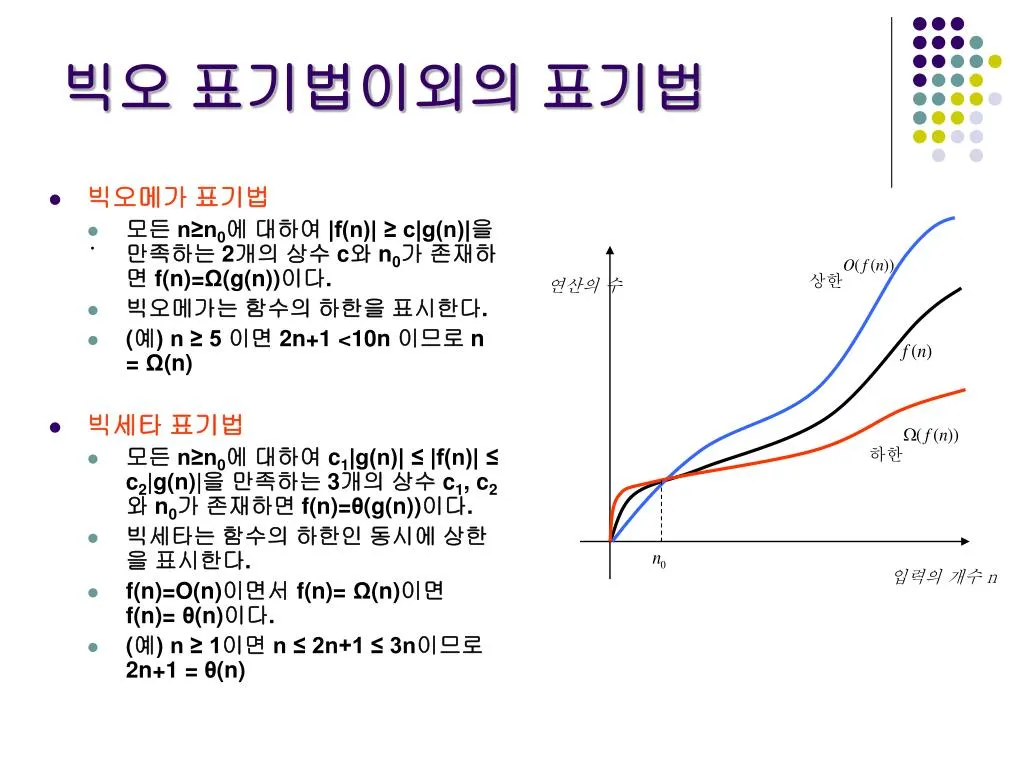
빅오 이외의 표기법

빅오메가 - 함수의 하한

빅세타 - 함수의 평균

실무를 수행할 때에는, n≥n_0인 모든 구간에서 어떤 알고리즘이 항상 우세한 것이 아닐 경우가 많고, 구간별로 성능이 다를 때가 많기 때문에, 우리가 사용할 구간에 따라서 알고리즘을 선택해야 하겠다.

최선/평균/최악의 경우 성능

알고리즘 수행시간은 입력자료집합이 어떠냐에 따라 다를 수 있음

(예시) 순차탐색

•

best case

찾고자 하는 숫자가 맨 앞에 있는 경우 O(1)

•

worst case

찾고자하는 숫자가 맨 뒤에 있는 경우 O(n)

•

average case

각 요소들이 균일하게 탐색된다고 가정 즉, n개의 자리 각각에 찾는 숫자가 놓일 확률이 동일하다고 가정하면 (1+2+...+n)/n = (n+1)/2 → O(n)

최선의 경우는 대부분 의미가 없고, 평균같은 경우는 매 case마다의 확률과 연산 횟수를 고려해야하기 때문에 계산이 매우 어렵기 때문에

최악의 경우(Big O)를 가장 널리 활용한다. 계산하기도 쉽고, 응용에 따라 중요한 의미를 가지기도 한다. ex. 비행기 관제 업무 - 최악의 경우를 고려해야 한다.

보통 최악의 경우와 평균적 경우를 함께 사용한다.

정렬?

record(정렬 대상인 원소)들을 순서대로 재배치하는 일

정렬시간 = 레코드 접근 시간 + 레코드 비교/재배체 시간

메모리 (Random Access Memory)

접근 속도가 빠르고, 부작위 접근이 가능하다

레코드 접근시간<<레코드비교시간

⇒ 레코드 비교시간이 정렬 성능의 척도가 된다⇒내부정렬

보조기억장치(CD, tape 등)

접근속도가 느리고, 접근이 제한적이다 ex) 데이터를 순차적으로 접근하는 것만 가능

레코드 접근시간 >> 레코드 비교시간

⇒ 레코드 접근시간(횟수)이 정렬 성능의 척도가 된다⇒외부정렬

내부정렬

•

모든 레코드가 RAM내에 존재한다고 가정

레코드 : 여러 데이터들로 구성된 Field들의 조합

Field 중 한 Field가 key역할을 해 이 key를 중심으로 오름차순/내림차순으로 정렬

Record = (Field1, Field2(=key), Field3, ... , Field_m)

ex) 학생기록 = (이름, 주민번호, 학번, 생년월일, 학기별 성적 등) → 학번순으로 오름차순/내림차순 정렬

내부정렬에서의 입력은 n개의 레코드들의 순열

정렬기준은 key

key를 기준으로 재배치된 레코드가 output

(강좌에선 특별한 언급 없으면 오름차순으로 정렬)

내부정렬 methods

Comparison-based Sorting method (비교 기반 정렬 알고리즘)

원소의 상대적 순서를 정할 때, 두 원소의 크기를 비교해서 정함

모든 비교 기반 정렬 알고리즘은 최소

\mathcal{O}(n \log n)

으로 실행

Selecting Sorting / bubble Sorting / Insertion Sorting

Shell Sorting

Quick Sorting / Merge Sorting / Heap Sorting

Distribution-based Sorting Method (분포 기반 정렬 알고리즘)

key범위가 한정되어있다는 가정 하에 key의 분포에 기반해 데이터를 재정렬

Counting Sorting / Radix Sorting / Bucket Sorting

정렬 알고리즘의 성능 측정(Performance Measure)

Time Complexity(average & worst cases)

•

Number of key comparison(비교기반정렬)

•

Number of record movement (분포기반정렬)

c.f. Number of external record access ( external sorting 외부정렬 )

Space Complexity

공간 복잡도 측면에서는, 원래 알고리즘 성능 측정에서 사용하는 빅오 표기법을 사용할 수는 있으나 보통 정렬알고리즘은 O(1)이나 O(n)로 표현돼 잘 사용하지 않는다.

•

In-place algorithm(제자리성)
고정된 메모리를 사용하는지, 가변적인 메모리를 사용하는지

•

In-place algorithm : 작고 일정한 크기를 갖는 외부 storage space의 data structure을 사용해 input을 변형하는 알고리즘(selection sort참고)
= 추가적인 메모리 공간을 많이 필요로 하지 않는 혹은 전혀 필요하지 않는 알고리즘을 의미한다. 즉, n 길이의 리스트가 있고, 이 리스트를 정렬할 때 추가적으로 메모리 공간을 할당하지 않아도 정렬이 이뤄진다면 in-place 알고리즘이라고 불릴 수 있는 것이다.

Stability

•

동일한 key값을 가지는 레코드들이 sorting 후에도 original records의 순서를 보존하는지 여부

•

정렬 알고리즘이 많은 알고리즘의 부분적인 알고리즘으로 쓰이기 때문에 큰 의미를 가질 수 있다.

•

list=[1, 7, 3, 5, 4, 7, 9]
이 리스트에서 7이 두번 나온다. 구분을 위해 ()를 이용해 앞은 (1), 뒤는 (2)를 표시하면
list=[1, 7(1), 3, 5, 4, 7(2), 9]와 같다.
이 리스트를 정렬했을 때
(1) list=[1, 3, 4, 5, 7(1), 7(2), 9](2) list=[1, 3, 4, 5, 7(2), 7(1), 9]
(1)처럼 나오면 안정(Stable) 정렬, (2)처럼 나오면 불안정(Unstable) 정렬이라고 한다.

•

Stable Sorting 알고리즘

◦

Insertion Sort

◦

Merge Sort

◦

Bubble Sort

◦

Counting Sort

•

Unstable Soring 

◦

Selection sort

◦

Heap Sort

◦

Shell Sort

◦

Quick Sort

정렬알고리즘들 종류별 설명

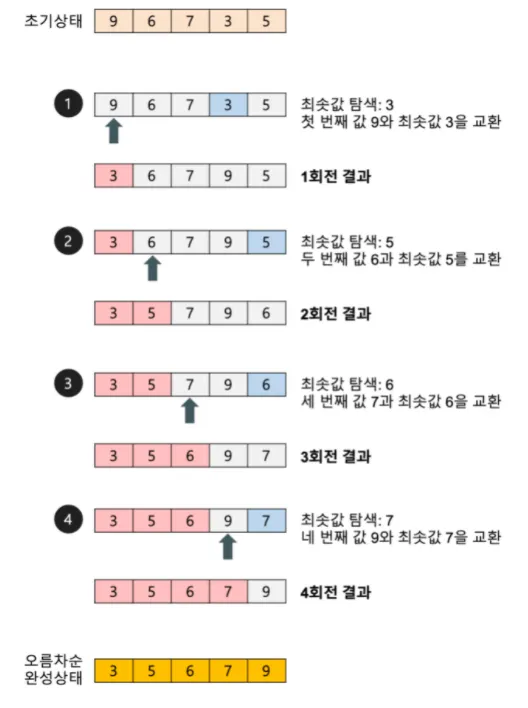
Selection Sort

<위키백과>

선택 정렬(選擇整列, selection sort)은 제자리 정렬 알고리즘의 하나로, 다음과 같은 순서로 이루어진다.

주어진 리스트 중에 최소값을 찾는다.

그 값을 맨 앞에 위치한 값과 교체한다(패스(pass)).

맨 처음 위치를 뺀 나머지 리스트를 같은 방법으로 교체한다.

비교하는 것이 상수 시간에 이루어진다는 가정 아래, n개의 주어진 리스트를 이와 같은 방법으로 정렬하는 데에는

\mathcal{O}(n^2)

만큼의 시간이 걸린다.

선택 정렬은 알고리즘이 단순하며 사용할 수 있는 메모리가 제한적인 경우에 사용시 성능 상의 이점이 있다.

•

i번째 단계에서 항상 n-i회의 비교를 수행하기 때문에

(n-1)+(n-2)+...+1=\frac{n(n-1)}{2}

평균시간복잡도 =

\mathcal{O}(n^2)

최악시간복잡도 =

\mathcal{O}(n^2)

•

inplace algorithm이다.(제자리 정렬)
i, j, MinIndex라는 정수형 변수(크기가 작고 일정한 자료형)가 사용되고, 추가로 사용되는 메모리가 없고, 기본적으로 상수크기 메모리만 사용하기 때문에, 제자리 정렬

•

unstable sorting algorithm이다.

<C코드>

# include <stdio.h>
# define SWAP(x, y, temp) ( (temp)=(x), (x)=(y), (y)=(temp) )
# define MAX_SIZE 5

// 선택 정렬
void selection_sort(int list[], int n){
  int i, j, least, temp;

  // 마지막 숫자는 자동으로 정렬되기 때문에 (숫자 개수-1) 만큼 반복한다.
  for(i=0; i<n-1; i++){
    least = i;
    // 최솟값을 탐색한다.
    for(j=i+1; j<n; j++){
      if(list[j]<list[least])
        least = j;
    }
    // 최솟값이 자기 자신이면 자료 이동을 하지 않는다.
    if(i != least){
        SWAP(list[i], list[least], temp);
    }
  }
}

void main(){
  int i;
  int n = MAX_SIZE;
  int list[n] = {9, 6, 7, 3, 5};

  // 선택 정렬 수행
  selection_sort(list, n);

  // 정렬 결과 출력
  for(i=0; i<n; i++){
    printf("%d\n", list[i]);
  }
}
C
복사

def selection_sort(arr):
    for i in range(len(arr) - 1):
        min_idx = i
        for j in range(i + 1, len(arr)):
            if arr[j] < arr[min_idx]:
                min_idx = j
        arr[i], arr[min_idx] = arr[min_idx], arr[i]
C
복사

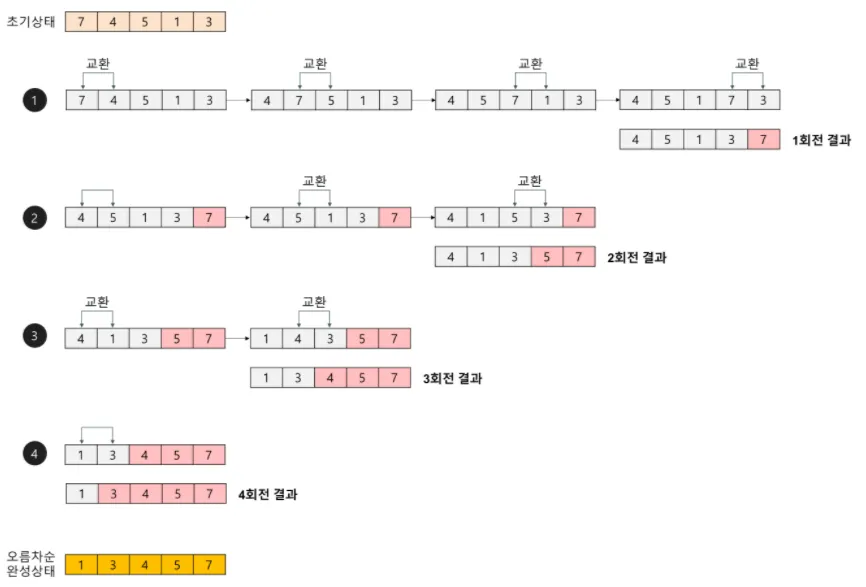
Bubble Sort

<위키백과>

거품 정렬 또는 버블 정렬은 두 인접한 원소를 검사하여 정렬하는 방법이다. 시간 복잡도가

\mathcal{O}(n^2)

로 상당히 느리지만, 코드가 단순하기 때문에 자주 사용된다. 원소의 이동이 거품이 수면으로 올라오는 듯한 모습을 보이기 때문에 지어진 이름이다. 양방향으로 번갈아 수행하면 칵테일 정렬이 된다.

•

인접한 2개의 레코드를 비교하여 크기가 순서대로 되어 있지 않으면 서로 교환한다.

•

인접한 레코드끼리만 자리를 바꾸므로 Stable Sort

•

i, Sorted등 상수 크기의 메모리만 사용하기 때문에 In-place Sort

•

시간복잡도
평균시간복잡도 = O(n2)\mathcal{O}(n^2)O(n2)
최악시간복잡도 = O(n2)\mathcal{O}(n^2)O(n2)
(ex) 최악의 경우 - 역순으로 정렬된 레코드
(n-1)+(n-2)+...+1=n(n-1)/2

<C코드>

#include <stdio.h>
# define MAX 10
# define SWAP(x, y, temp) ( (temp)=(x), (x)=(y), (y)=(temp) )

// 1회전이 아닌 전체 회전에 해당하는 함수(배열길이 n이므로 (n-1)회전 결과)
int* bubble_sort(int arr[], int n) {
    int i, j, temp;
    for (i=n-1; i>0; i--) { // 9~1 9번
        for (j=0; j<i; j++) {// 0~8, 1~7, 2~6, ..., 0
            if (arr[j] > arr[j+1]) { // 오름차순
                SWAP(arr[j], arr[j+1], temp);
            }
        }
    }
    return arr;

}// 포인터로 하는 이유가 몰까?.?-> 공간적 효율성? 원래 배열은 제거?
// Q1. SWAP에서 주소값 교환(SWAP(&arr[j], &arr[j+1])과 이렇게 bubble_sort함수의 리턴값 자료형 자체를 포인터로 하는 것이 같은 것인지?
// Q2. 왜 포인터변수? 포인터형?으로 지정하는지? 장점이 뭔지?

int main() {
    int arr[MAX] = { 2, 6, 4, 8, 10, 12, 89, 68, 45, 37 };
    int* arr_new = bubble_sort(arr, MAX);
    for (int i = 0; i < MAX; i++) {
        printf("%d\n", *(arr_new+i));
    }
    return 0;
}ㄴ
C
복사

<Python코드>

def bubbleSort(x):
	length = len(x)-1
	for i in range(length):
		for j in range(length-i):
			if x[j] > x[j+1]:
				x[j], x[j+1] = x[j+1], x[j]
	return x
C
복사

좀 더 효율적인 Bubble SORT 설계

bubble sort 스텝을 다 돌기 전에 이미 정렬이 다 되어있는 경우

초기 배열 30 20 40 10 5 10 30 15
1회전: 20 30 40 10 5 10 30 15→20 30 40 10 5 10 30 15→20 30 10 40 5 10 30 15→20 30 10 5 40 10 30 15 → 20 30 10 5 10 40 30 15→20 30 10 50 10 30 40 15 → 20 30 10 5 10 30 15 40
2회전: (생략) → 20 10 5 10 30 15 30 40
3회전: (생략) → 10 5 10 20 15 30 30 40
4회전: (생략) → 5 10 10 15 20 30 30 40
5회전: (생략) → 5 10 10 15 20 30 30 50
6회전: (생략) → 5 10 10 15 20 30 30 50
7회전: (생략) → 5 10 10 15 20 30 30 50

사실상 5회전부터는 생략해도 된다

<C코드>

#include <stdio.h>
# define MAX 10
# define SWAP(x, y, temp) ( (temp)=(x), (x)=(y), (y)=(temp) )

// 1회전이 아닌 전체 회전에 해당하는 함수(배열길이 n이므로 (n-1)회전 결과)
// 한 회전에서 SWAP함수가 한번도 호출되지 않으면 회전을 멈춘다.
int* bubble_sort(int arr[], int n) {
    int i, j, temp, Sorted;
		Sorted = FALSE;
    for (i=n-1; i>0; i--) { // 9~1 9번
		  While(!Sorted){
					Sorted = TRUE;
					for (j=0; j<i; j++) {// 0~8, 1~7, 2~6, ..., 0
		        if (arr[j] > arr[j+1]) { // 오름차순
		          SWAP(arr[j], arr[j+1], temp);
	           }
					}
	     }
	   }
    return arr;
}
    

int main() {
    int arr[MAX] = { 2, 6, 4, 8, 10, 12, 89, 68, 45, 37 };
    int* arr_new = bubble_sort(arr, MAX);
    for (int i = 0; i < MAX; i++) {
        printf("%d\n", *(arr_new+i));
    }
    return 0;
}
C
복사