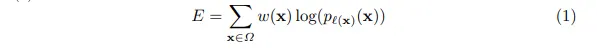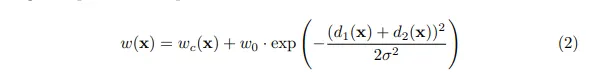💗

U-Net

U-Net: Convolutional Networks for Biomedical Image Segmentation

There is large consent that successful training of deep networks requires many thousand annotated training samples. In this paper, we present a network and training strategy that relies on the strong use of data augmentation to use the available annotated samples more efficiently.

https://arxiv.org/abs/1505.04597

Abstract

•

존재하는 annotated samples를 더 효율적으로 사용하여 적극적인 data augmentation 활용에 의존하는 training 방법과 네트워크를 소개한다

•

이 아키텍쳐는 context를 포착하기 위한 contracting path와 정확한 localization을 가능하게 하는 대칭적인 expanding path로 이루어져 있다.

•

우리는 이런 네트워크가 매우 적은 이미지들로도 end-to-end로 학습될 수 있고, 이전의 ISBI challenge for segmentation of neuronal structures in electron microscopic stacks에서의 최고의 방법(sliding window convolutional network)보다 더 뛰어난 성능을 보인다는 것을 보여준다.

•

transmitted light microscopy images(phase contrast and DIC)에서 학습된 같은 네트워크를 사용하여서 우리는 2015 ISBI cell tracking challenge에서 이 카테고리들에서 큰 차이로 우승했다.

•

또한, 이 네트워크는 빠르다. 512x512 이미지 task에서 최근의 GPU로 1초보다 덜 걸린다. 

Introduction

Biomedical tasks : output이 classification 뿐 아닌 위치정보 포함해야하며 대부분의 상황에서 training image 수가 적다. 또한 같은 클래스 객체들이 접촉해 있는 경우가 많음

⇒ 단순 classification만을 수행하는 기존의 CNN으로는 부족

이 논문 이전에 biomedical image processing을 위해 localization 정보를 얻는데에 sliding window를 사용해 모든 픽셀의 크래스를 예측하려는 시도가 있었다.

sliding window의 장점

localization 가능

patch data를 사용하기 때문에 data가 많다.

sliding window의 단점

redundancy of over lapping patch(겹치는 패치의 불필요한 중복성)위의 사진에서 보이는 것과 같이 patch를 옮기면서 중복이 발생하게 된다.

이 중복된 부분은 이미 학습된(검증된) 부분을 다시 학습하는 것이므로 똑같은 일을 반복하는 것과 같다. 즉, 불필요한 중복에 대한 내용도 학습하기 때문에 속도도 느리고 시간도 오래 걸린다.

trade-off between localization accuracy and use of context : patch 사이즈가 크면, max pooling이 더 많이 적용 되고 정확한 위치 정보를 알기에는 어렵지만, 더 넓은 범위의 이미지를 보기 때문에 context 인식에는 효과를 가진다.

이에 대한 U-Net의 해결 : 중복되지 않은 patch를 검증해 속도를 개선

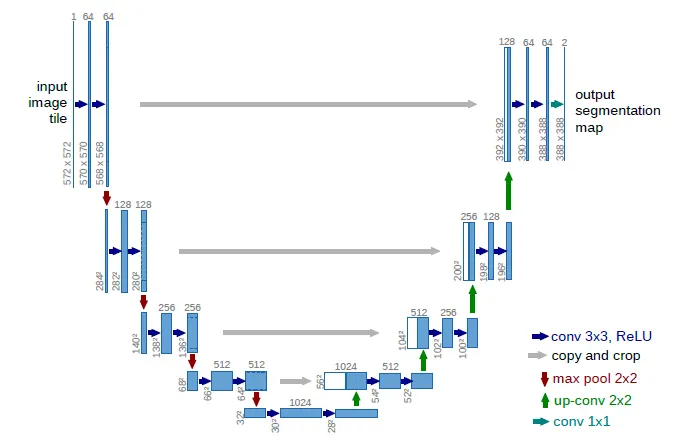
Network Architecture

이렇게 반씩 두 파트로 나눌 수 있다.

Contracting Path

{ 3x3 conv(unpadded) + ReLU } x 2+ 2x2 max pooling(downsampling의 목적)이 반복됨

downsampling할 때 마다 feature 채널 수는 2배로 증가

Expansive Path

2x2 conv(up - convolution) + contracting path에서 해당하는 피쳐맵과의 concat + { 3x3 conv(unpadded) + ReLU } x 2

upconv를 거치면 채널 수는 절반으로 줄어든다

마지막 레이어는 1x1 conv 레이어로 각 64 component feature vector에 적용된다. 클래스 개수에 맞추기 위한 레이어 이다.

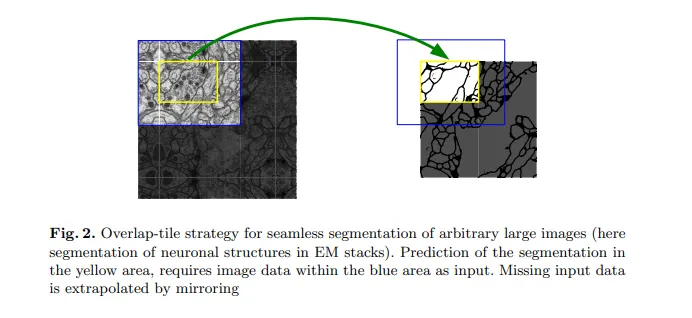
Fig2 : output segmentation map의 원활한 타일링(tiling)을 가능하게 하기 위해, 2x2 max-pooling operations이 균일한 x및y 크기 레이어에 적용되도록 input tile size를 정하는 것이 중요

Fig 2의 노란 영역의 segmentation을 위해서는 파란색 영역의 input이 필요하다

input data에서 잃는 부분은 mirroring으로 채워짐

Training

unpadded conv → input보다 작은 output

overhead 최소화 + GPU 최대 사용 위해서는 큰 batch size에서 큰 input tiles를 사용해서 하나의 이미지에 대한 batch를 줄이는게 좋다.

따라서

아주 많은 이전에 본 traning samples가 현재의 optimization step에서 업데이트를 결정할 수 있도록 높은 momentum(0.99)를 사용한다

Energy function 은 cross entropy loss function과 합쳐져 마지막 피쳐맵에 대한 pixel wise softmax로 계산된다.

softmax :

p_k(x) = \exp(a_k(x))/\sum_{ \acute{k}}^{K}\exp(a_{\acute{k}}(x))

a_k(x)

: pixel위치

x\in \Omega

와

\Omega \subset Z^2

의 feature channel k의 activation

K : class 개수

p_k(x)

: approximated maximum-function

즉, maximum activation

a_k(x)

를 갖는

k

에 대하여

p_k(x) \approx1

반대로 다른

k

에 대하여

p_k(x)\approx0

cross entropy는

p_{l(x)}(x)

의 deviation에서 각 위치마다 penalize

w

: weight map (특정 픽셀에 더 중요성을 주기 위한 가중치)

각각의 ground segmentation대해서 weight map

w

을 계산해서 network가 인접한 세포들 사잉의 얇은 경계(separation border)를 알아내도록 한다.

weight map 수식

w_c:

weight map to balance the class frequencies

d_1

: distance to the border of the nearest cell

d_2

: distance to the border of the second nearest cell

d1, d2

의 경우 세포이미지에 대한 논문이다 보니 이런 용어가 나오는듯

w_0

= 10,

\sigma

= 5 ( 실험적으로 세팅 )

이 w를 활용한 weighted loss는 touching cell들간의 경계를 구할 수 있게 해준다

deep network 에서는 weight의 초기값 설정이 중요하다 → std가

\sqrt{2/N}

인 Gaussian 분포로부터 뽑아냄 (N: 하나의 뉴런에 들어오는 노드의 수 E.g. 64 feature 채널 갖는 3x3 conv의 경우 이전레이어 N=9x64=576)

Data Augmentation

몇 안되는 트레이닝 데이터가 있는 경우 원하는 invariance와 robustness properties를 위해서 Data Augmentation은 필수적

microscopical images의 경우 우리는 주로 invariance의 shift와 rotation이 필요하다 gray value variations와 deformations에 대한 robustness뿐만 아니라

Especially random elastic deformations of the training samples seem to be the key concept to train a segmentation network with very few annotated images.

특히 몇 안되는 annotated images로 segmentation을 학습시킬 떄에는 training samples 의 random elastic deformations가 핵심으로 보인다.

우리는 거친 3x3 그리드에서 무작위 변위 벡터(random displacement vectors)를 사용하여 부드러운 변형을 생성한다. 변위(displacements)는 10픽셀 표준 편차를 갖는 가우스 분포에서 샘플링된다. 그런 다음 픽셀당 변위는 바이큐빅 보간을 사용하여 계산된다. 계약 경로 끝에 있는 드롭아웃 계층은 암시적 데이터 증가를 수행합니다. - elastic deformation 내용

Experiments

U-Net 성능 테스트 위해 3가지 segmentation task에 적용

task 1: segmentation of neuronal structures in electron microscopic recordings (EM segmentation challenge at ISBI 2012)

U-net는 pre- / postprocessing 없이 warping error에서 best score를 얻었다.

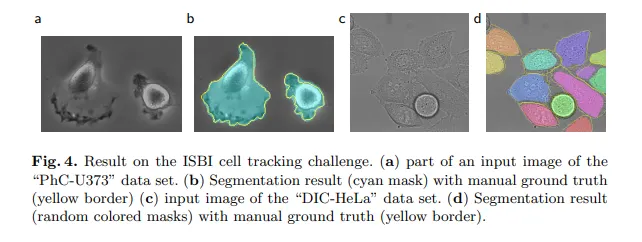
task 2, 3: cell segmentation task in light microscopic images (ISBI cell tracking challenge 2014 and 2015)

U-net는 서로 다른 dataset에 대해 각각 92%, 77.5%의 IOU(intersection over union)를 얻었다.

두개의 dataset에 대한 u-net segmentation result 예시

Conclusion

•

U-net 구조는 많은 biomedical segmentation application에서 좋은 성능을 보인다.

•

Elastic deformation을 통한 data augmentation으로 많은 training image가 필요하지 않다.

•

Training 시간도 매우 합리적