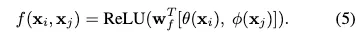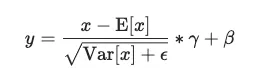Carnegie Mellon University & Facebook AI Research
발표자료
•
convolution, recurrent operations → 한번에 one local neighborhood만을 처리
•
non local operation을 long rage dependencies를 포착하기 위한 일반적 building blocks로 소개
•
컴퓨터비전의 classical non-local means 방법에서 영감을 받아 이 논문의 non-local operation은 한 포지션에서 모든 포지션의 피쳐들의 가중합의 response를 계산
•
이 building block은 많은 컴퓨터비전 아키텍쳐들에 적용될 수 있음
•
Kinetics 와 Charades dataset에서 SOTA 달성
•
static image recognition에서 우리의 non local models는 object detection / segmentation / pose estimation에서 성능 향상을 이뤘다.
Introduction
capturing long-range dependencies : deep neural network에서 핵심적으로 중요한 부분
sequential data ( speech, language )에 대해서는 recurrent operations(LSTM같은거)가 주요 솔루션.
이미지데이터에 대해서는 conv연산을 깊게 쌓아서 큰 receptive field를 이룸으로써 long rage dependencies가 모델링된다.
convolution / recurrent operations 모두 local neighborhood를 처리하는 연산( 시간 혹은 공간영역에서 )
그래서 long range dependencies는 이 연산들이 반복해서 적용되는것으로만 포착할 수 있었다.
반복연산 → 비효율적 & 최적화의 어려움 & 모델링시 multi-hop dependency 발생
논새하이한제느하새 운로 -ocnallcaalepataion은 피쳐맵의 모든 영역의 피쳐를 weighted sum형식으로 더해준다
특히 비디오 분류에서 3D / 2D conv보다 좋은 성능을 보였다
object detection / segmentation / pose estimation에도 적용시 성능이 전반적으로 향상되어 이 연산이 일반성을 가짐도 증명한다
Non-local means Filter
랜덤 노이즈 ⇒ 랜덤한 특성을 띄는 노이즈 ⇒ 매번 영상을 촬영할때마다 촬영하고자 하는 대상은 그대로 있지만, 노이즈는 랜덤하게 변함
랜덤 노이즈가 제거된 영상을 얻고자 할때는
1.
동일한 사진을 여러 차례에 거쳐 촬영하고
2.
이들 사진을 합쳐서 평균을 내주면
⇒ 랜덤한 특성은 사라지고 우리가 원하는 사물만 깨끗하게 남아있는 영상을 얻을 수 있습니다.
하지만 동일한 영상을 여러차례에 거쳐서 촬영하는 것은 상당히 귀찮은 일이고 때론 불가능 할 수도 있습니다.
이를 극복하고자 NLM Filter는 한 장의 영상만을 가지고 기존의 노이즈 제거 방법과 같은 원리를 이용하여 노이즈를 제거합니다.
자세히 살펴보면 대체로 한 장의 영상 안에도 서로 유사한 영역들이 상당히 많이 존재합니다.
예시) 위 사진에서 p 지점의 경우 p의 위 아래에 q1, q2와 같이 p와 유사한 구조의 지점들이 존재합니다. 때문에 한 영상 안에서도 이러한 유사한 영역들을 모아준 후 평균을 취해주면 여러장의 영상을 평균해 준 결과와 유사한 결과를 얻을 수 있습니다.
이러한 원리를 이용하는 NLM Filter는 노이즈를 제거하는데 있어서 여타 다른 필터들에 비해 상당히 좋은 성능을 보여줍니다.
NLM이라는 이름에서 드러나듯이 다수의 필터들과 가장 다른 주안점은 영상의 주변부 (local) 만을 이용한 것이 아니라 영상 전체 영역 (non-local)을 활용한 필터라는 것이었습니다.
이러한 특성 덕분에 NLM Filter는 한동안 가장 좋은 성능을 가진 노이즈 제거 필터였고, 현재까지도 가장 좋은 노이즈 제거 필터로 인정되고 있는 BM3D 필터 역시도 NLM의 원리를 차용하고 있습니다.
영상 전체 영역, 즉 non-local한 영역에서, 서로간의 유사도를 측정하고 이를 활용
Non-local Neural Network
3.1. formulation
generic non-local operation
= input signal
= 와 크기 같은 output signal
= index of an output position
= pairwise function으로, i와 모든 j 사이 scalar값을 계산한다 ( affinity같은 relationship을 나타낸다 )
단일 함수 = input signal의 j위치에서의 representation을 계산한다. 기존 NLM에서는 해당 위치 픽셀값을 가져오는 부분일 것이지만 이 block에서는 그냥 위치값을 가져오는 것이 아니라 임베딩을 통해 좀 더 의미있는 정보를 추출한다
이렇게 나온 response는 factor 로 normalize된다
이 식이 왜 non-local 이냐면 모든 위치 가 연산에 포함되기 때문이다
비교적으로
•
convolution 연산은 local neighborhood ( i-1 ≤ j ≤ i+1 )에서의 input의 weighted sum을 합친 것이고
•
recurrent operation은 한 시점 i가 오직 현재와 가장 마지막 time step인 경우가 많다
non-local operation은 fc layer와도 다르다.
fc는 단순 weight를 학습하고 고정된 크기의 input과 ouput이 필요하며 위치적 관계를 잃지만 이 식은 다른 위치들 사이의 관계에 기반하기 때문이다
3.2. Instantiations
여기선 f와 g의 여러 버전을 묘사한다
간단화를 위해 g를 linear embedding의 형식으로 고려한다 (는 weight matrix)
이는 1x1 conv혹은 1x1x1conv와 같이 적용할 수 있다
f로 선택 가능한 것들
1.
Gaussian
non-local mean과 bilateral filters를 따라 자연스러운 선택은 가우시안이다. 이 논문에서는 이렇게 고려하였다
는 dot-product similarity이다. Euclidian distance도 적용할만 했지만 dot product가 최근 딥러닝 플랫폼에서 더 구현하기 적합해서 사용했다고 한다. normalize factor는 이렇게 정의된다
가우시안 분포 식
2.
Embedded Gaussian
단순한 가우시안의 확장이다. embedding space에서 similarity를 계산한다. 이 논문에서는 위의 식과 같이 고려한다
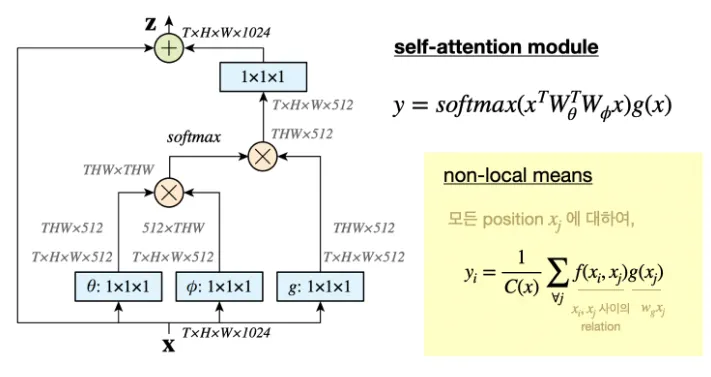
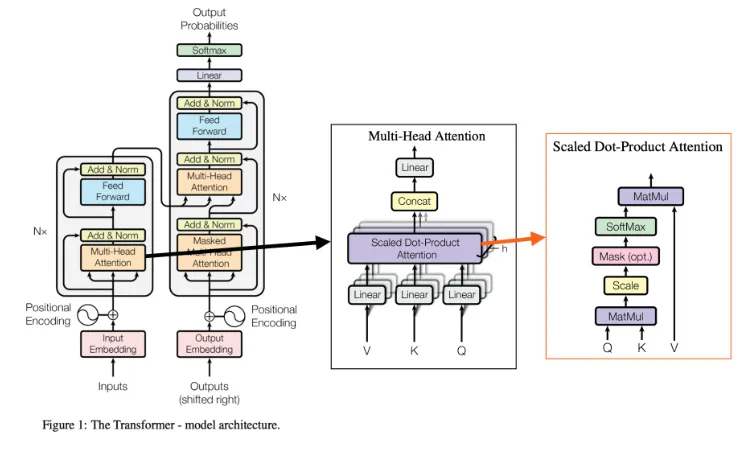
self attention module ( [49] : Attention is All you need - 트랜스포머 논문에서 나온 모듈 )이 최근 machine translation을 위해 최근 발표되었고, 이는 embedded Gaussian version에서의 non-local operation의 스페셜케이스임을 주목하였다
이는 주어진 i에 대해서 가 dimension 방향으로 softmax연산이 된다는 점에서 보여진다.
그래서 [49]의 self attention module을 다음과 같이 정의했다
그런식으로, 이 연구는 self-attention model을 classic computer vision method인 non local means를 연관시키는 인사이트를 제공하는 동시에 sequential self-attention network[49]를 일반적인 이미지 혹은 피디오 인식을 위한 space/spacetime non-local network로 일반화한다
[49]와의 관계에도 불구하고 attention behavior (softmax때문에) 은 이 논문의 연구의 적용에 필수적이지는 않음을 보여준다 . 이를 보여주기 위해서 non local 연산의 두가지 대안을 보여준다
Non-local operations의 대안
1.
Dot Product
dot product similarity의 수식
embedded version을 적용하였으며 normalize factor는 으로 세팅했다. 은 의 위치들의 수이다. gradient computation을 단순화시키기 위해 들의 합 대신 이것으로 대체했다.
이러한 normalization은 input size가 다양하기에 필수적이다
dot product와 embedded Gaussian versions의 주요 차이점은 softmax의 유무이며 softmax는 activation의 역할을 한다
2.
Concatenation
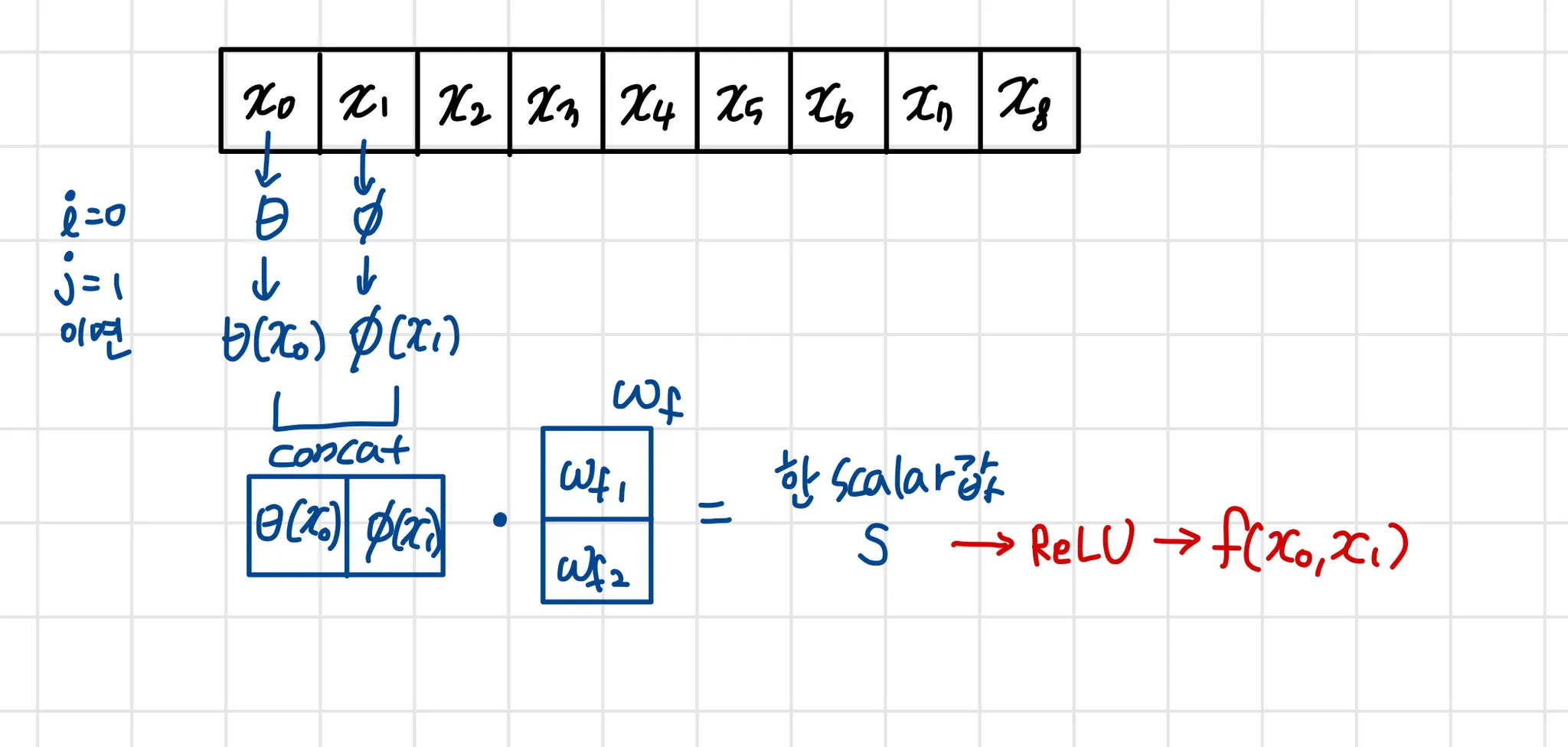
concatenation은 Relation Networks에서 visual reasoning을 위해 pairwise function으로 사용되었다
이 concatenation 연산을 말한다
는 concatenated vector를 scalar로 project해주는 weight vector이다.
위에서처럼 이다
이러한 다양한 변형들은 이 논문의 generic non-local operation의 flexibility를 입증한다고 한다
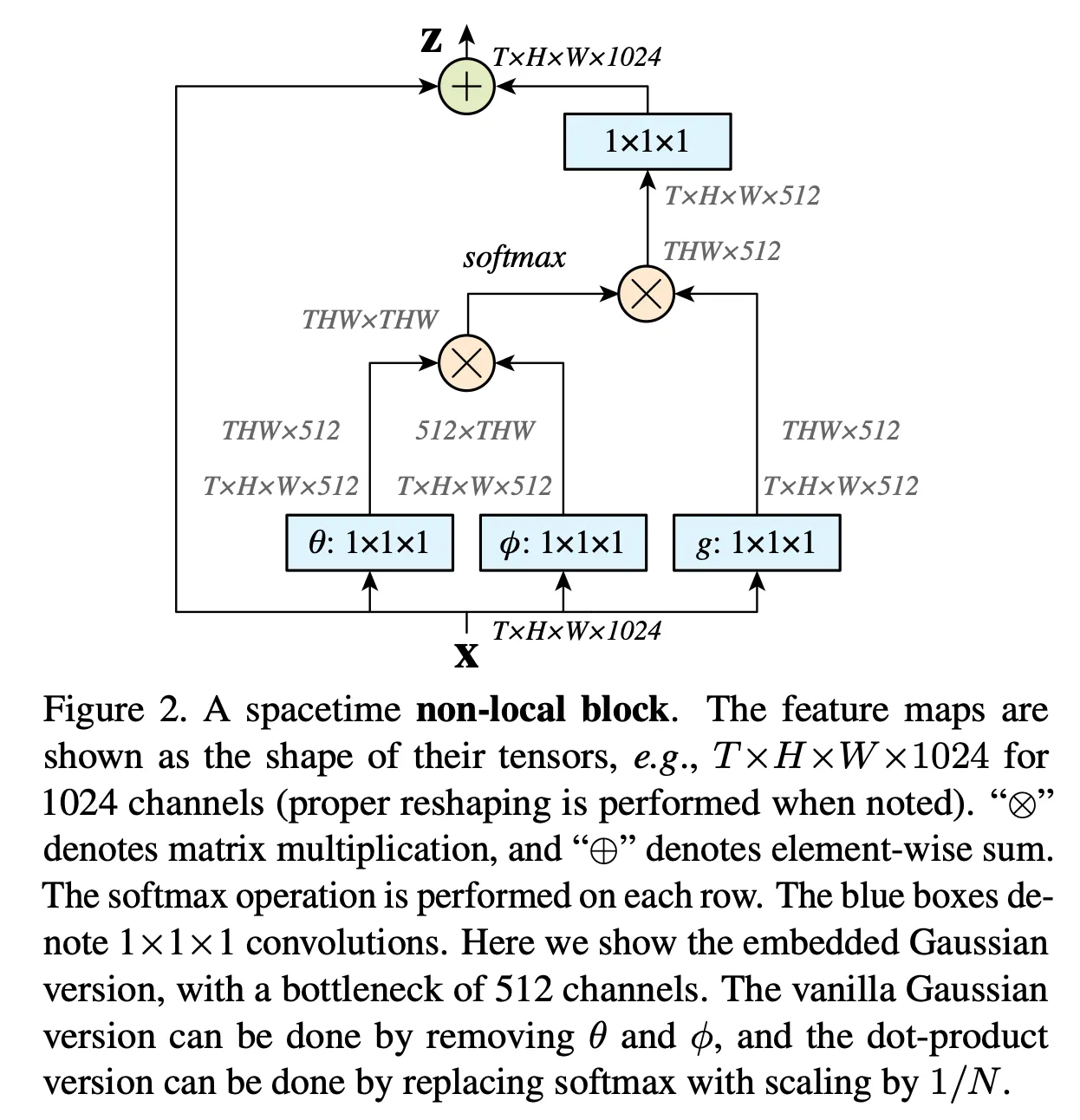
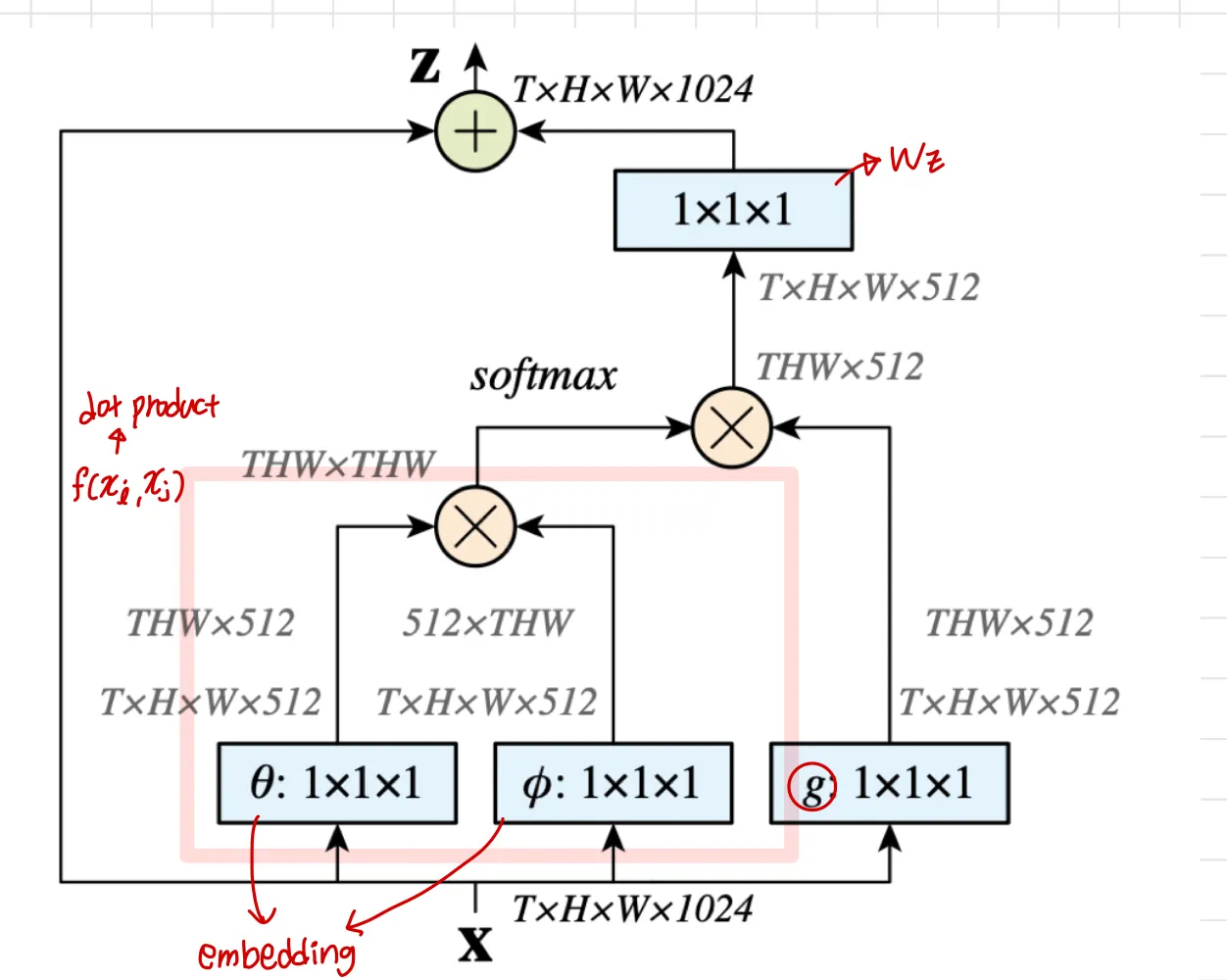
3.3. Non-local Block
앞에서 언급한 이 식을 다양한 아키텍쳐에 적용했다고 함
non-local block을 다음과 같이 정의한다
는 residual connection을 의미한다
그림과 같이 , Gaussian, Embedded Gaussian, Dot product는 단순히 matrix곱으로 적용되었다
softmax의 경우에는 embedded Gaussian 형태로 f를 계산할 때 dot product로 두 벡터의 유사도 계산 결과에 exponential 적용 후 C(x)로 normalize ( f의 합 )하면 결국 softmax와 동일하기 때문에 이렇게 적용한 것입니다
마지막에 residual 적용을 위해 1x1 conv로 채널을 맞춰준 후 residual 합을 해줍니다.
그림에는 나와있지는 않으나 element-wise sum 전에 1x1x1conv 직후 BN 적용하였습니다
BN의 scaling factor 인 gamma초기값 0으로 적용하였는데, 이미 학습 완료한 CNN에 이 block을 추가하는 방식으로 학습시켰기 때문에, non local block이 학습초기에는 반영되지 않다가 점점 서서히 반영되도록 하기 위해 이렇게 적용하였습니다.
이 블럭의 pairwise computation은 lightweight를 갖고 high level에서 subsampled feature map에 사용하면 lightweight를 갖는다
Fig2의 일반적 값은 이다
matrix multiplication으로 수행되는 pairwise computation은 일반적인 convolution 레이어와 견줄만하다
Implementation of Non-local Block
의해 나오는 피쳐맵의 채널수는 입력 채널수의 절반으로 했다
concatenate부분에 나오는 는 에 pointwise embedding을 연산해 채널수를 input에 맞춘다.
subsampling trick은 연산을 줄이는데 활용될 수 있다
가 subsampled version of 이며, 간단히 말하면 원래 모든 픽셀과의 관계를 연산했으나 subsampling한 몇몇의 픽셀들과의 관계만을 연산하는 것이다 ( pooling 등을 통해 )
이렇게 해서 연산을 1/4로 줄였다고 하며,
이 trick은 non-local behavior를 대체하는 것이 아니라 오직 연산을 sparser하게 만든다
이는 와 이후에 maxpooling레이어를 더하는 것으로 수행되었다
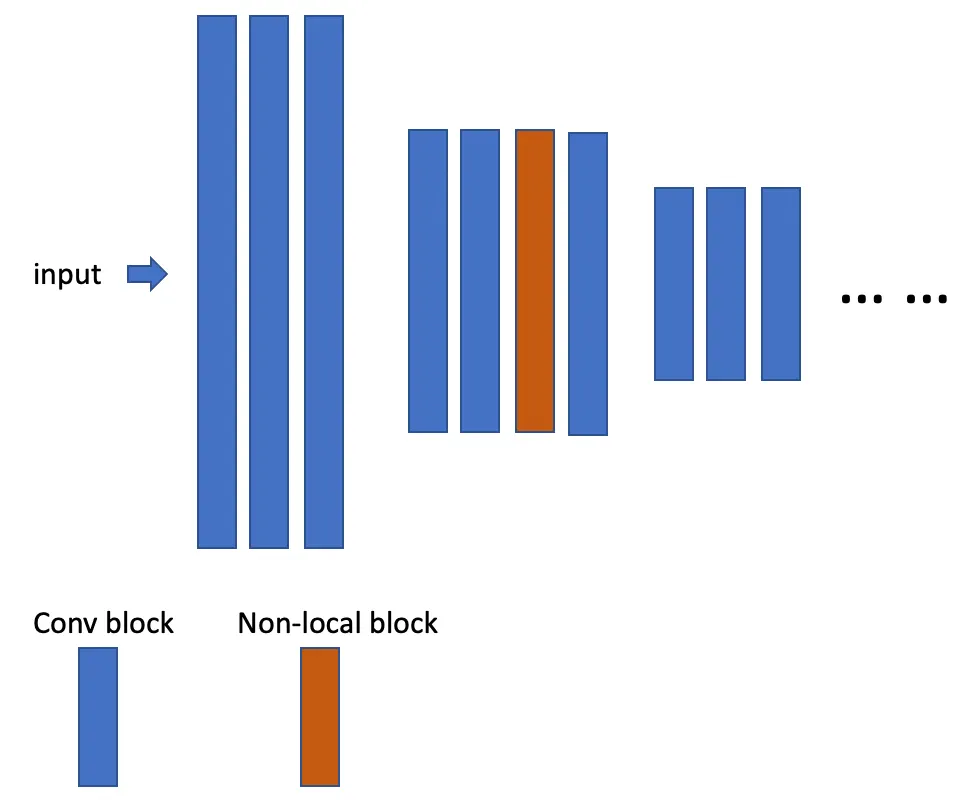
이런식으로 삽입된다
Experiments
Kinetic dataset : 비디오 분류 챌린지 2017
비디오에서 사람이 어떠한 행동을 하고 있는지 맞추기
C2D모델(ResNet50기반)과 I3D모델 활용
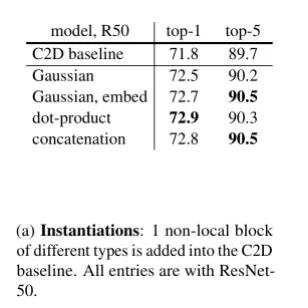
여러 형태의 f 비교
C2D의 마지막 residual block바로 이전에 non-local block 삽입
어떤 식을 사용하던 큰 영향은 없었다. 각 위치간 관계를 정의만 해준다면 성능 향상에 도움이 된다는 점을 알 수 있다.
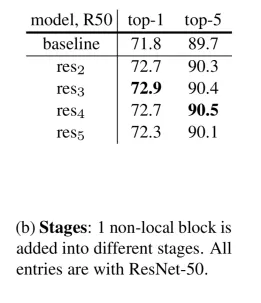
어느 위치에 non local block을 삽입해야할까
너무 마지막보다는 좀 더 앞에 배치하는 것이 좋은 성능을 보였다
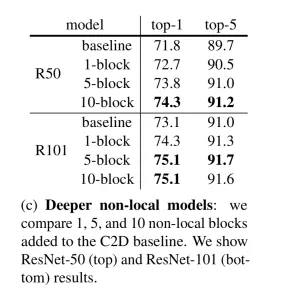
얼마나 삽입해야할까
더 많이 넣을수록 성능이 올라가지만 ResNet101같은 경우 5개나 10개나 별 차이가 없어서 적정 개수를 찾아주는 것이 좋아보입니다
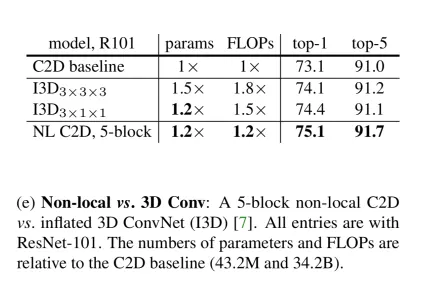
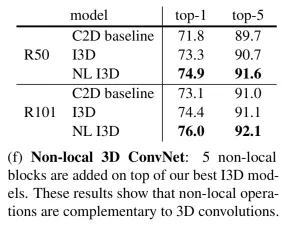
Non local Network vs 3D network
시간축을 제한적으로 볼 수 밖에 없었던 C2D모델에 non local block을 사용하면 더 좋은 성능을 낼 것임을 기대할 수 있었습니다
그러나 I3D같은 경우에는 시간축 정보를 적극적으로 활용하는 모델이기 때문에 이 모델로 비교해보면
C2D에 non local block을 사용한 모델이 I3D보다 파라미터/연산은 더 적게 하면서도 성능은 더 우수하였습니다
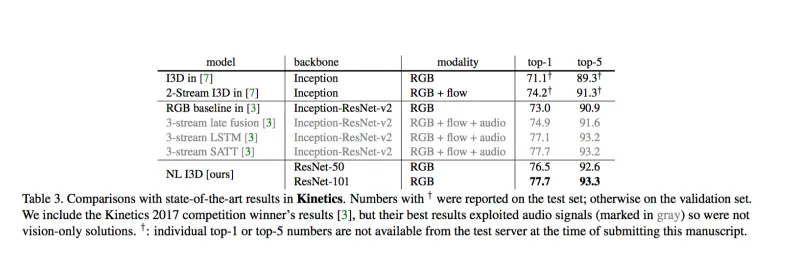
I3D모델 성능
competition결과
Conclusion
이 논문에서는 long-range dependency를 잡을 수 있는 새로운 non-local operation을 제안한다. 이 operation을 wrap up한 block은 기존에 학습되어 있는 네트워크의 중간중간에 들어갈 수 있으며, 이미 학습되어있는 baseline network에 이 block을 더했을 때 유의미한 성능향상이 있었음을 확인할 수 있었다.