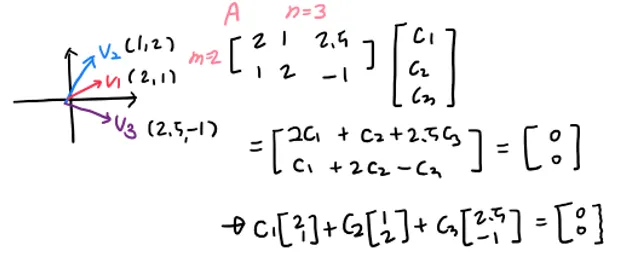independence (독립)
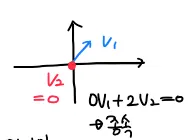
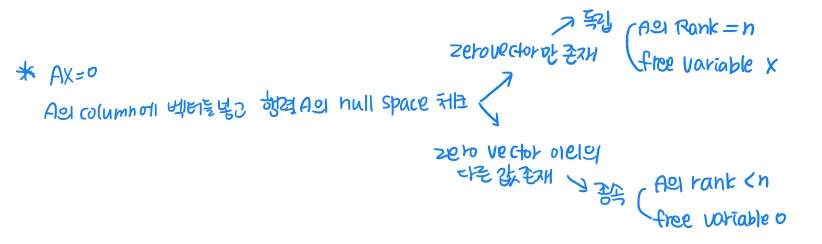
벡터 이 있을 때 모든 계수 가 0인 경우를 제외하고 어떤 선형조합으로도 0을 만들지 못하는 경우 이 벡터들은 독립이라고 한다.
⇒ except for all
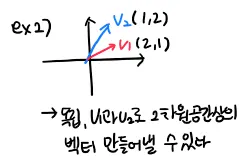
⇒ 2차원 상에 존재하는 벡터들이지만 1차원만을 정의할 수 있음
ex3)
이 경우에는 미지수 > 방정식 개수 이다. (m<n) 이 경우 null space가 존재하므로 종속이다.
미지수가 방정식 개수보다도 많음에도 null space가 존재하는 이유
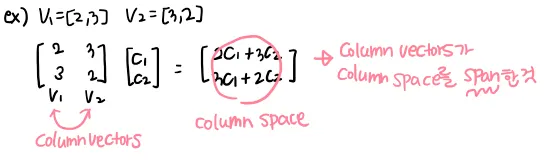
span
span은 사전적 의미로 “포괄하다”이다. 이에 연결지어 생각해보면 “주어진 벡터들로 형성할 수 있는 공간”, “주어진 벡터들의 선형결합으로 만들어지는 공간”정도로 생각할 수 있겠다.
span a space 로 많이 표현된다.
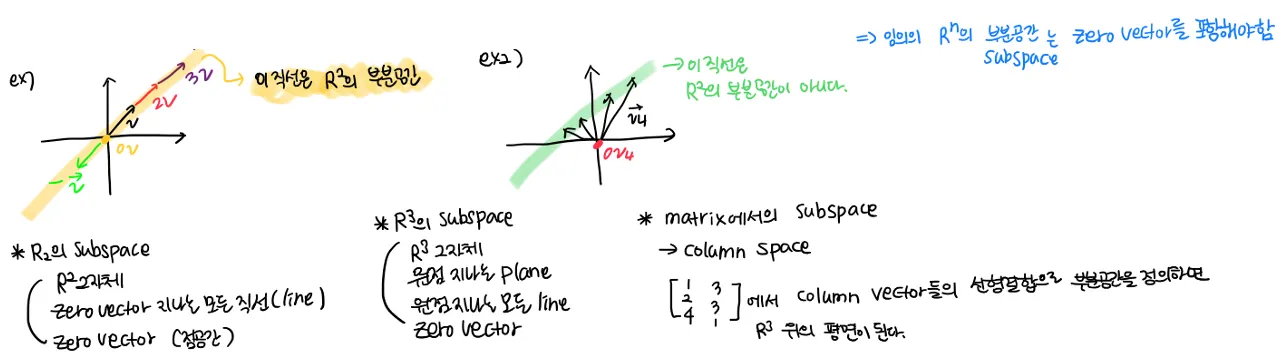
subspace
vector space란 무엇일까 : 다수의 벡터가 모여 생성한 공간. 다수의 벡터들이랑 선형겨랗ㅂ이 가능한 같은 공간상의 벡터들.
그렇다면 subspace란 무엇일까
같은 space내의 벡터들은 동일 공간상의 벡터들의 선형결합으로 정의될 수 있어야 한다고 했다.
그런데 만약 다음과 같은 경우라면 어떨까?
⇒ subspace는…
이 안의 n차원 벡터들끼리 선형결합 연산이 성립하고 그 결과 또한 그 공간에 속해야 한다.
Basis (기저)
: 어떤 공간을 span하면서 서로 독립인 벡터들
basis는 어떻게 알 수 있을까?
: vectors → column vectors → 가우스소거 → echelon form → free variable 갖는가, 모든 column vector가 pivot을 갖는가 (rank로 판별)
에 대해 n개의 벡터가 있을 때 이들이 basis vectors이려면 nxn의 역행렬이 존재해야 한다.
= 의 basis는 3개의 3차원 벡터가 존재해야하며 3x3 역행렬이 존재한다.
= 3차원 벡터 3개로 구성되면서 독립이면 무조건 의 basis이다.
참고
Dimension (차원)
N차원의 space에 대해 basis는 무수히 많다.
⇒ 주어진 space 내에 모든 basis는 같은 수의 벡터를 가지며 그 수가 dimension이다.