Search

Focal Loss

•
Distribution based loss 중 하나
•
object detection 모델인 RetinaNet 논문에서 소개됨
•
foreground 와 background의 심한 class imbalance를 해결하기 위해 Cross Entropy를 변형
•
잘 분류되었을 때 Loss값이 감소하도록 한다

어렵거나 오분류 되는 케이스에 더 큰 가중치를 준다

Class Imbalance 발생 시 문제점

1.
쉽게 background로 분류될 수 있는 easy negative는 학습에 비효율적
2.
easy negative 각각의 loss 값은 작으나(background로 잘 분류되기 때문에) 클래스의 비율이 너무 커 (배경이 대부분을 차지) 전체 loss 및 gradient에 영향을 크게 미치게 된다.

기존 Cross Entorpy의 문제점

잘 분류한 경우에는 초점을 두지 않고, 잘못 예측한 경우 페널티를 부여하는 것에만 초점을 두기 때문에, easy example일 경우, 즉 잘 분류되었을 때의 보상이 전혀 없습니다. 잘 분류되었을 때 loss가 감소하지는 않는다는 것이죠

ex) BCE

BCE=−y(log⁡(p))−(1−y)(log⁡(1−p))BCE = -y(\log (p)) -(1-y)(\log(1-p))
이 경우 y=1일 때, (정답이 1일 때 ) CE(y,p)=−ylog⁡(p)CE (y, p) = -y\log(p) 가 됩니다.
•
p=1p=1일경우 : CE(y,p)=0CE(y, p)=0 으로 페널티가 사라지지만, 보상도 없습니다
•
p≈0p\approx0 일 경우 : CE(y,p)≈∞CE(y, p)\approx\infty 로, 페널티가 매우매우 커집니다

ex) BCE, Y=1 (foreground), p=0.95 케이스와 Y=0(background), p=0.05의 case

•
CE(foreground)=−log⁡(0.95)=0.05CE(foreground) = -\log(0.95)=0.05
•
CE(background)=−log⁡(1−0.05)=−log⁡(0.95)=0.05CE(background) = -\log(1-0.05)=-\log(0.95)=0.05
•
⇒ foreground와 background 모두 잘 분류하였으나, 같은 Loss값을 가진다
•
⇒ 이렇게되면 background의 케이스가 훨씬 많음에도 불구하고 foreground와 같은 비율로 loss가 업데이트되어 background에 대해 학습이 훨씬 많이 될 것이고, 누적되어 foreground에 대한 학습량이 상대적으로 매우 줄어들게 된다.

weighted cross entropy(WCE)의 한계

WCE는 기존에 class imbalance 문제를 해결하기 위해 사용되어 왔습니다.
예를 들면, foreground 객체의 클래스 수와 background 객체의 클래스 수 각각의 역수를 weight로 사용한다면 클래스 수가 많은 background의 경우 loss가 작게 반영되고, 클래스 수가 적은 foreground의 경우 비교적 크게 반영될 것입니다.
WCE(pt)=−wt(log(pt))WCE(p_t) = -w_t(log(p_t))
foreground 의 weight는 크게, background의 weight는 작게 적용해 문제를 해결하는 것 같아 보이지만, 단순히 개수가 많다고 easy example이라 판단하거나, 단순히 개수가 적다고 hard example이라 판단할 수는 없기 때문에, Easy / Hard Example 판단이 어렵습니다.
예) 0이 background, 1이 foreground로 분류하며, foreground에 0.8의 weight를, background에 0.2의 weight를 주는 경우
•
foreground일 확률 p=0.95, 정답이 1
◦
WCE(foreground)=−0.8log⁡(0.95)=0.017WCE(foreground) = -0.8\log(0.95)=0.017
•
foreground일 확률 p=0.05, 정답이 0 ( 0으로 잘 분류하였기 때문에 확률 낮음)
◦
WCE(foreground)=−0.2log⁡(1−0.05)=−0.2log⁡(0.95)=0.004456WCE(foreground) = -0.2\log(1-0.05) = -0.2\log(0.95)=0.004456
⇒ easy / hard example에 대한 고려는 없다

Focal Loss

“Cross Entropy + Hard Example에 대해서 초점”
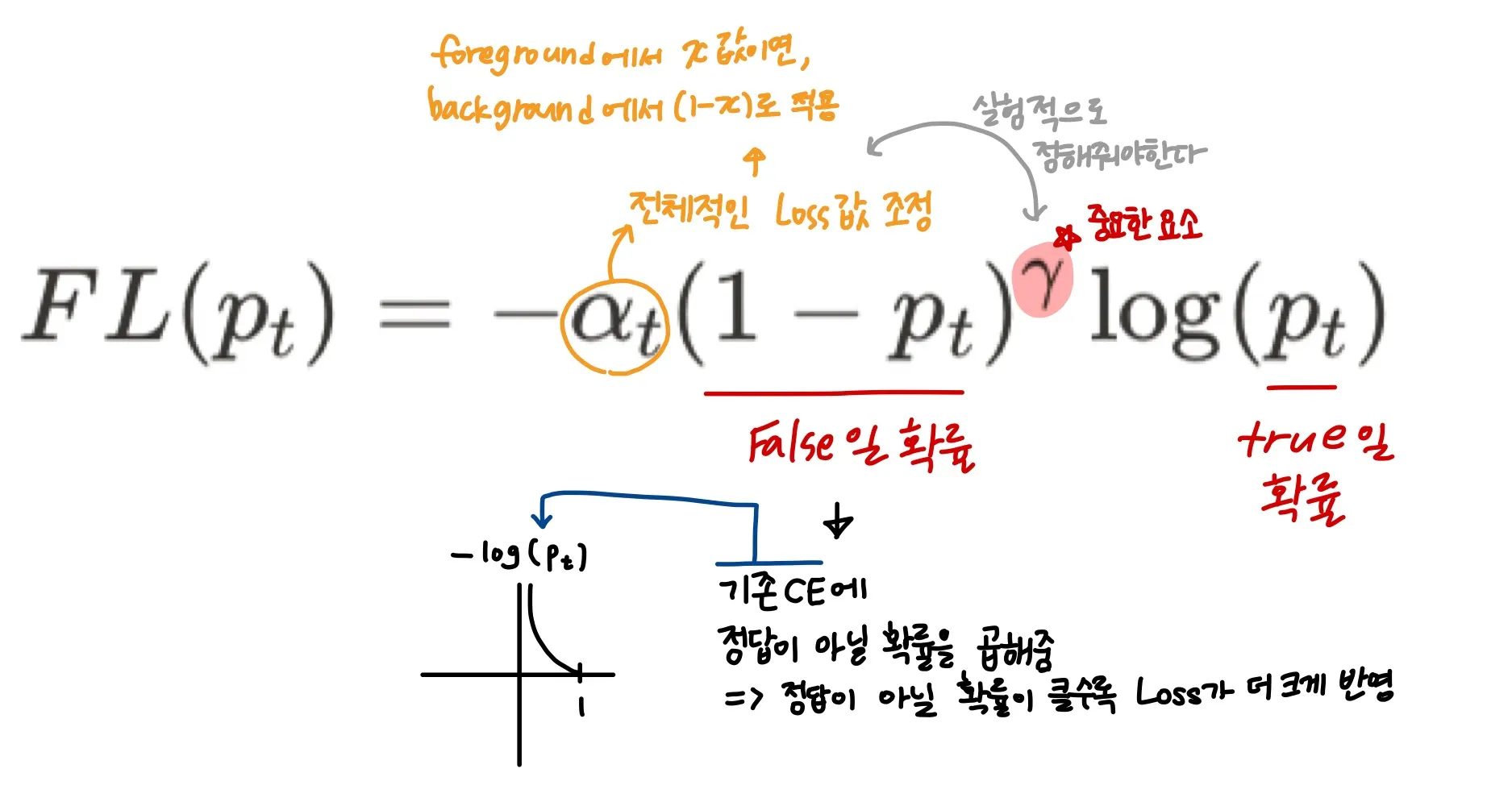
FL(pt)=−αt(1−pt)γlog⁡(pt)FL(p_t)=-\alpha_t(1-p_t)^\gamma \log(p_t)
RetinaNet 논문에서는 αt=0.25,γ=2\alpha_t=0.25, \gamma=2 로 최종적으로 사용했다
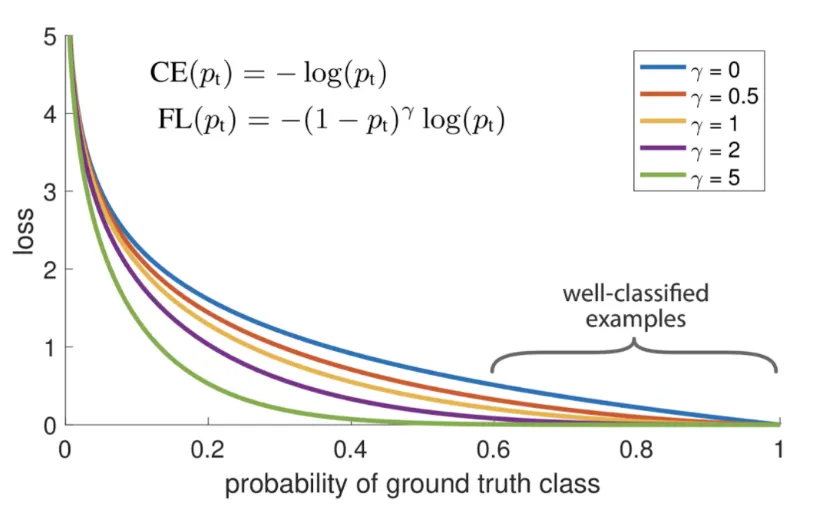
gamma에 따른 FL의 변화, γ=0\gamma=0이면 CE와 같음
그래프를 보면 γ\gamma를 크게 설정할수록 잘 분류되는 example들, 즉 easy example들에 대한 loss값은 매우 줄어든다

식과 그래프를 통해 알 수 있는 Focal Loss의 특징

•
잘못 분류됨 ⇒ ptp_t가 작음 ⇒ (1−pt)(1-p_t)가 커짐 즉, 1에 가까워짐, log⁡(pt)\log(p_t) 는 커짐
•
잘 분류됨 ⇒ ptp_t가 큼 ⇒ (1−pt)(1-p_t)는 작아짐 즉, 0에 가까워짐, log⁡(pt) \log(p_t) 는 작아짐
•
γ\gamma = focusing parameter : easy example의 loss에 대한 비중을 낮추는 역할 ( 커질수록 easy example의 loss값이 작아진다 )

실제 값을 넣어 확인해 보는 hard example과 easy example의 차이

< α=1,γ=1\alpha = 1, \gamma = 1 이라고 가정 → FL(pt)=−(1−pt)log⁡(pt)FL(p_t)=-(1-p_t)\log(p_t) >
CE
FL
pt=0.1p_t = 0.1 (hard case)
−log⁡(0.1)≈2.3-\log(0.1)\approx2.3
−(1−0.1)log⁡(0.1)≈2.1-(1-0.1)\log(0.1)\approx2.1
pt=0.9p_t = 0.9 (easy case)
−log⁡(0.9)≈0.1-\log(0.9)\approx0.1
−(1−0.9)log⁡(0.9)≈0.01-(1-0.9)\log(0.9)\approx0.01
hard case에서 FL과 CE 차이는 0.2밖에 나지않지만 easy case에서는 FL이 CL의 1/10배가 되어버린다
⇒ Easy Negative가 너무 많아 loss가 누적되어 값이 커지는 문제를 개선할 수 있게 된다.

구현

Made with