크루스칼 알고리즘은 대표적인 최소 신장 트리를 찾는 알고리즘이다.
신장트리
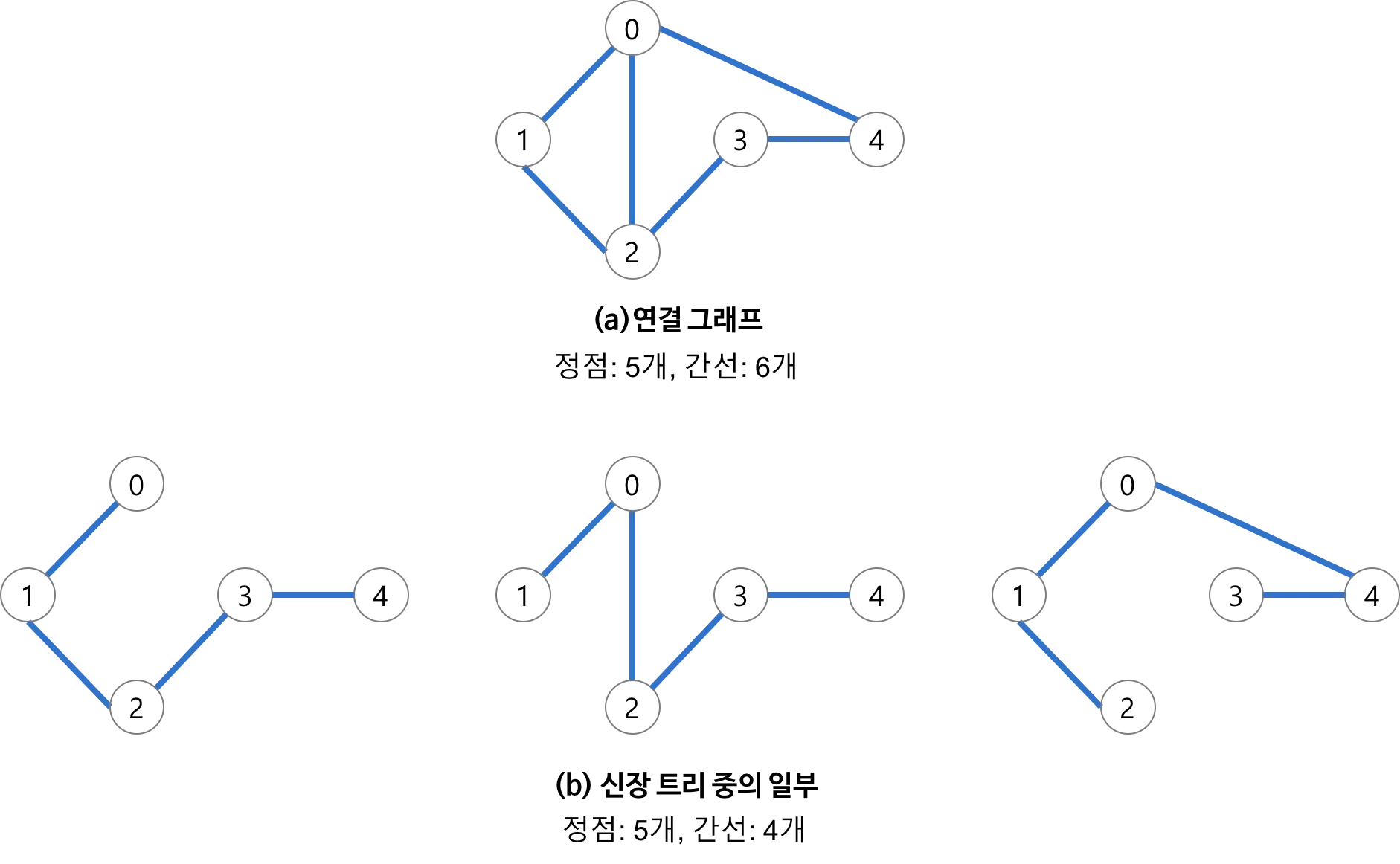
그래스에서 모든 노드를 포함하면서 사이클이 존재하지 않는 부분그래프
모든 노드가 포함되어 서로 연결되며 사이클이 존재하지 않는 것은 트리라고도 할 수 있다.
신장트리의 간선 수는 (노드수 -1)개이다. (트리의 기본적 특성)
위 그림의 (a)처럼 사이클이 존재하는 경우는 신장트리라고 할 수 없다.
최소신장트리 문제
최소한의 비용으로 구성되는 신장트리를 찾는 문제이다.
ex) N개의 도시가 존재할 때
•
두 도시 사이 도로를 놓아 전체 도시가 서로 연결되도록 도로를 설치하는 경우
•
모든 도시를 최소한의 비용으로 방문하는 경우
크루스칼 알고리즘
•
최소신장트리 알고리즘
•
그리디 알고리즘
•
동작과정
1.
간선 데이터를 비용에 따라 오름차순 정렬 ⇒ 비용이 적은 간선부터 확인
2.
간선 하나씩 확인하면서 현재의 간선이 사이클을 발생시키는지 확인
•
사이클 발생 x인 경우 : 최소 신장 트리에 포함
•
사이클 발생 시 : 최소 신장 트리에 포함 x
3.
모든 간선에 대해 2번 반복
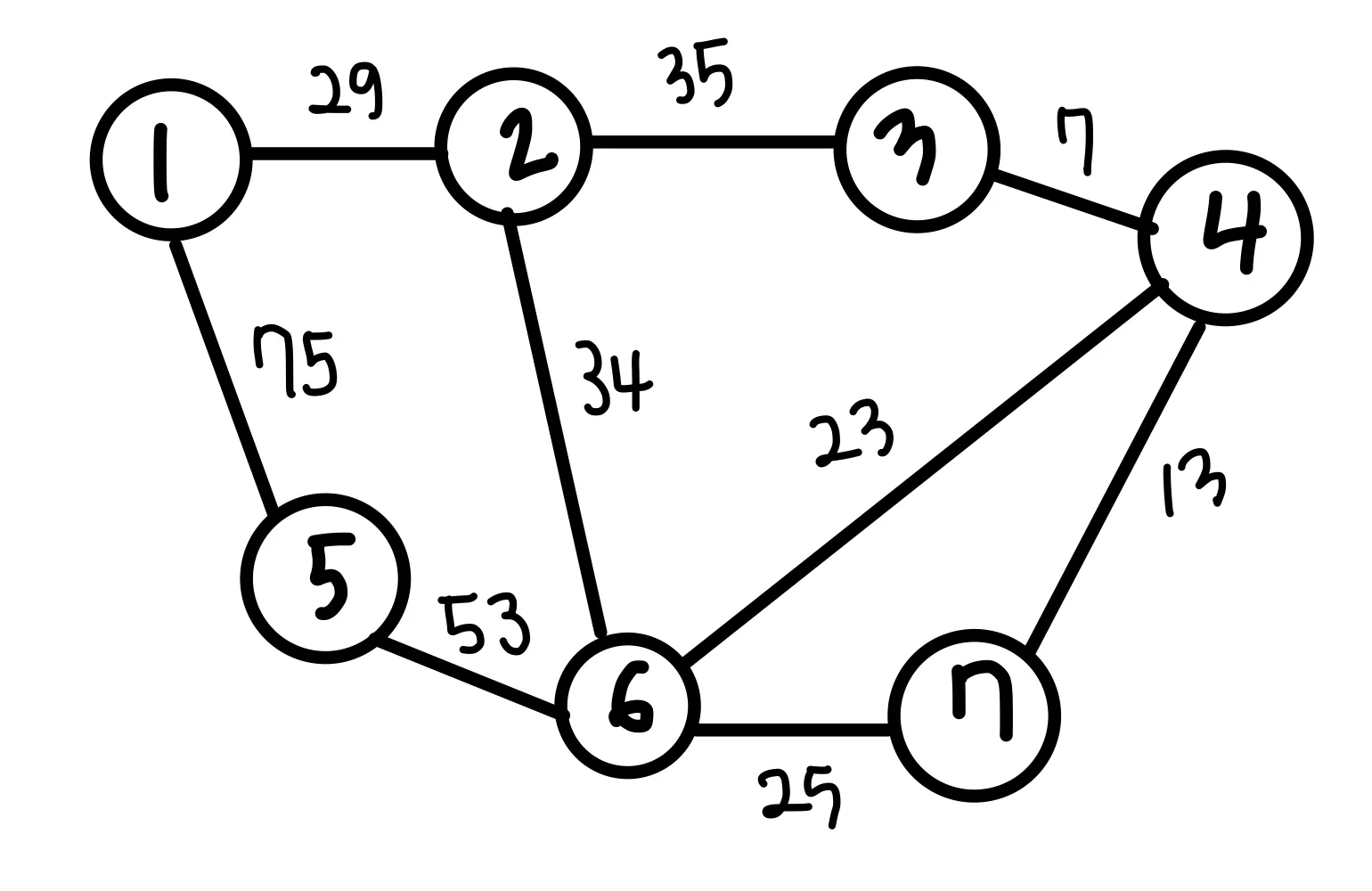
예시
간선 | (1,2) | (1,5) | (2,3) | (2,6) | (3,4) | (4,6) | (4,7) | (5,6) | (6,7) |
비용 | 29 | 75 | 35 | 34 | 7 | 23 | 13 | 53 | 25 |
(1)오름차순 정렬
간선 | (3,4) | (4,7) | (4,6) | (6,7) | (1,2) | (2,6) | (2,3) | (5,6) | (1,5) |
비용 | 7 | 13 | 23 | 25 | 29 | 34 | 35 | 53 | 75 |
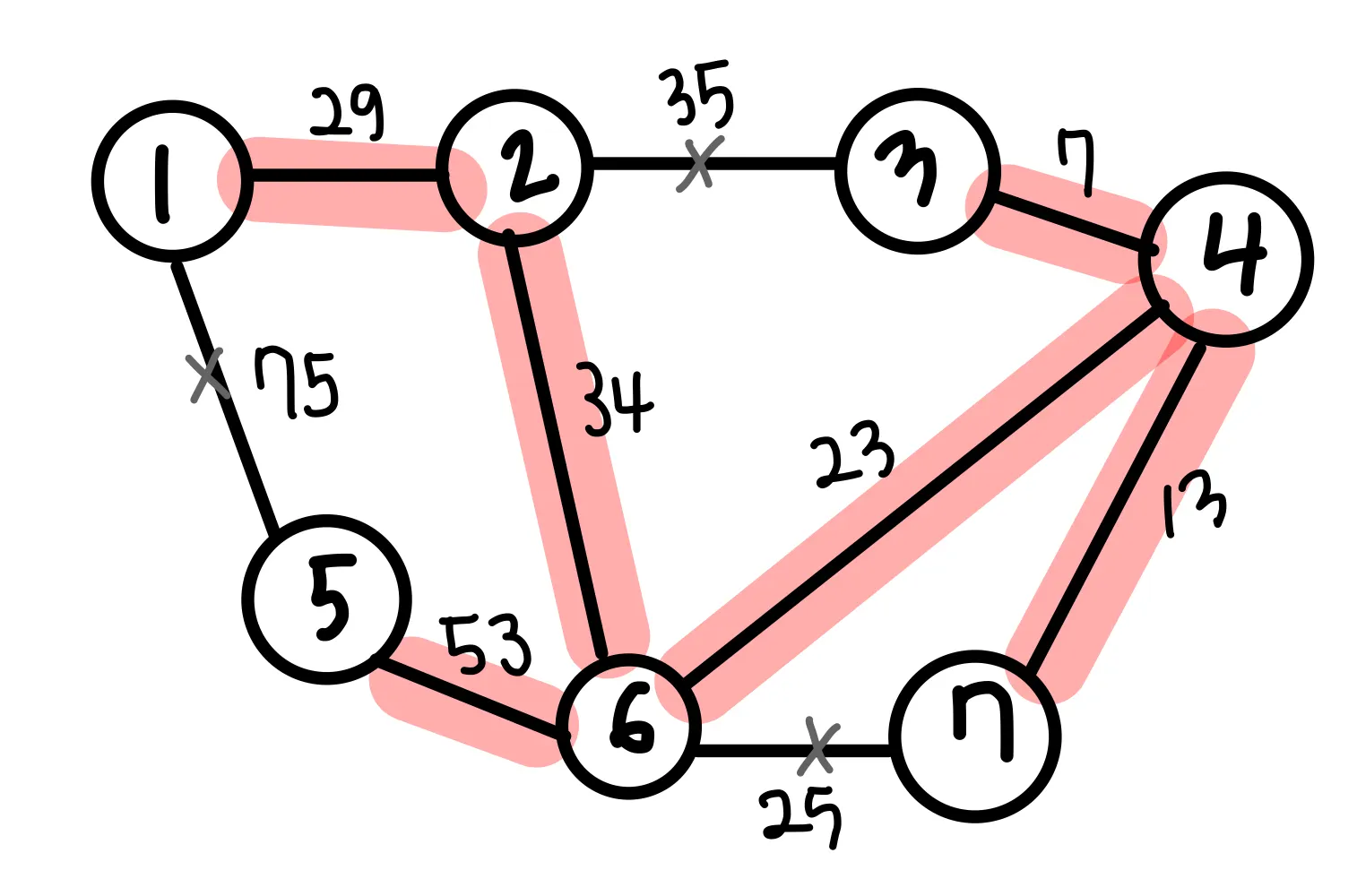
(2)
(3, 4) → 두 노드가 같은 집합에 속하여있지 않으므로 union 함수 수행
(4, 7) → union
(4, 6)→ union
(6, 7) → cycle 발생!! pass
(1, 2) → union
(2, 6) → union
(2, 3) → cycle 발생 !! pass
(5, 6) → union
(1, 5) → cycle 발생 !! pass
code
# https://github.com/ndb796/python-for-coding-test/blob/master/10/5.py
# 특정 원소가 속한 집합을 찾기
def find_parent(parent, x):
# 루트 노드가 아니라면, 루트 노드를 찾을 때까지 재귀적으로 호출
if parent[x] != x:
parent[x] = find_parent(parent, parent[x])
return parent[x]
# 두 원소가 속한 집합을 합치기
def union_parent(parent, a, b):
a = find_parent(parent, a)
b = find_parent(parent, b)
# 큰쪽에 대한 부모를 작은쪽으로 설정
if a < b:
parent[b] = a
else:
parent[a] = b
def solution(v, e, edges):
parent = list(range(v+1))
result = 0
# 간선을 비용순으로 정렬
edges.sort()
# 간선을 하나씩 확인하며
for edge in edges:
cost, a, b = edge
# 사이클이 발생하지 않는 경우에만 집합에 포함
if find_parent(parent, a) != find_parent(parent, b):
union_parent(parent, a, b)
result += cost
return result
Python
복사
(2) for edge in edges 반복문 부분을 살펴보기
(3, 4) :
•
a=3 b=4 cost=7
•
find_parent(parent, a)→3
•
find_parent(parent, b)→4
•
union함수로 parent[4]는 3이 됨
•
parent : [0, 1, 2, 3, 3, 5, 6, 7]
•
result = 7
(4, 7)
•
a=4 b=7 cost=13
•
find_parent(parent, a) → 3
•
find_parent(parent, b) → 7
•
union함수로 parent[7]은 3이 됨
•
parent: [0, 1, 2, 3, 3, 5, 6, 3]
•
result = 20
(4, 6)
•
a=4 b=6 cost=23
•
find_parent(parent, a) → 3
•
find_parent(parent, b) → 6
•
union함수로 parent[6]은 3이 됨
•
parent: [0, 1, 2, 3, 3, 5, 3, 3]
•
result = 43
(6, 7)
•
a=6 b=7 cost=25
•
find_parent(parent, a) → 3
•
find_parent(parent, b) → 3
•
두 노드가 속하는 트리의 루트가 3으로 같으므로 ( 같은 집합에 속하므로) cycle 발생 → pass
(1, 2)
•
a=1 b=2 cost=29
•
find_parent(parent, a) → 1
•
find_parent(parent, b) → 2
•
union함수로 parent[2]은 1이 됨
•
parent: [0, 1, 1, 3, 3, 5, 3, 3]
•
result = 72
(2, 6)
•
a=2 b=6 cost=34
•
find_parent(parent, a) → 1
•
find_parent(parent, b) → 3
•
union함수로 parent[3]은 1이 됨
•
parent: [0, 1, 1, 1, 3, 5, 3, 3]
•
result = 106
(2, 3)
•
a=2 b=3 cost=35
•
find_parent(parent, a) → 1
•
find_parent(parent, b) → 1
•
두 노드가 속하는 트리의 루트가 1로 같으므로 ( 같은 집합에 속하므로) cycle 발생 → pass
(5, 6)
•
a=5 b=6 cost=53
•
find_parent(parent, a) → 5
•
find_parent(parent, b) → 1
◦
찾는 과정에서 parent[6]이 1이 됨
•
union함수로 parent[5]은 1이 됨
•
parent: [0, 1, 1, 1, 3, 1, 1, 3]
•
result = 159
(1, 5)
•
a=1 b=5 cost=75
•
find_parent(parent, a) → 1
•
find_parent(parent, b) → 1
•
두 노드가 속하는 트리의 루트가 1로 같으므로 ( 같은 집합에 속하므로) cycle 발생 → pass
⇒ ⇒ result = 159