한장정리
백트래킹 Backtracking
백트래킹은 해결책에 대한 후보 구축하다 가능성이 없다고 판단되는 후보를 포기(backtrack)해 정답을 찾아가는 알고리즘으로 제약 충족 문제에 유용하다.
제약충족문제
DFS에서는 항상 백트래킹이라는 단어가 나온다
백트래킹은 DFS보다 좀 더 광의의 의미를 갖는다.
백트래킹은 탐색을 하다가 더 갈 수 없으면 왔던 길을 되돌아가 다른 길을 찾는다는데서 유래했다. 백트래킹은 DFS와 같은 방식으로 탐색하는 모든 방법을 뜻하며, DFS는 백트래킹의 골격을 이루는 알고리즘이다.
이또한 주로 재귀로 구현한다.
•
알고리즘마다 DFS의 변형이 조금씩 있긴 하지만, 기본적으로 모두 DFS의 범주이다
•
백트래킹은 가보고 되돌아오기를 반복한다
•
운이 좋으면 시행착오를 덜 거치고 목적지에 도착하지만 최악의 겨우 모든 경우를 다 거친 후 도착한다
⇒ 브루트포스(brute force)와 유사
•
한번 방문 후 가능성이 없는 경우에는 즉시 후보를 포기하기 때문에 매번 같은 경로를 방문하는 브루트포스보다는 훨씬 우아한 방식
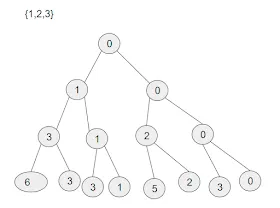
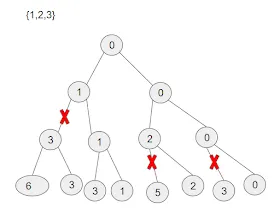
다음과 같이 가능성이 없는 후보는 즉시 포기하고 백트래킹하는 방식으로 트리의 불필요한 부분을 버린다.
이를 “가지치기(pruning)” 라고 한다
불필요한 부분을 일찍 포기 == 탐색을 최적화 ⇒ 가지치기는 탐색의 최적화 문제와도 관련이 깊음
코테에서 자주 쓰이는 DFS 템플릿
완전탐색
n, m = map(int,input().split())
def recur(cur):
if cur == n:
print(arr)
return
for i in range(m):
arr[cur] = i
recur(cur + 1)
recur(0)
Python
복사
순열 : 이미 사용한 숫자는 사용하지 않음
n, m = map(int,input().split())
visited = [False] * m
arr = [0] * m
def recur(cur):
if cur == n:
print(arr)
return
for i in range(m):
if visited[i]:
continue
visited[i] = True
arr[cur] = i
recur(cur + 1)
visited[i] = False
recur(0)
Python
복사
조합 : 이미 사용한 숫자 사용하지 않고 사용한 순서도 고려하지 않음 (ex. 123==132)
n, m = map(int,input().split())
arr = [0] * m
def recur(cur, start):
if cur == n:
print(arr)
return
for i in range(start, m):
arr[cur] = i
recur(cur + 1, i + 1)
recur(0,0)
Python
복사