Tree : 계층형 트리 구조를 시뮬레이션 하는 추상자료형(ADT)으로, 루트값과 부모-자식 관계의 서브트리로 구성되며, 서로 연결된 노드의 집합이다.
•
하나의 뿌리에서 위로 뻗어나가는 형상이라서 트리라는 이름이 붙었으나, 트리구조 표현에는 나무의 형상과 반대 방향으로 표시한다.
•
족보, 조직도 등을 트리구조라고 할 수 있음
•
재귀로 정의된(Recursively Defined) 자기참조(Self-Referential) 자료구조이다. 흔히 서브트리(subtrees)로 구성된다고 표현한다
•
이러한 재귀적 특성으로 트리에서는 재귀 순회가 좀 더 자연스럽다
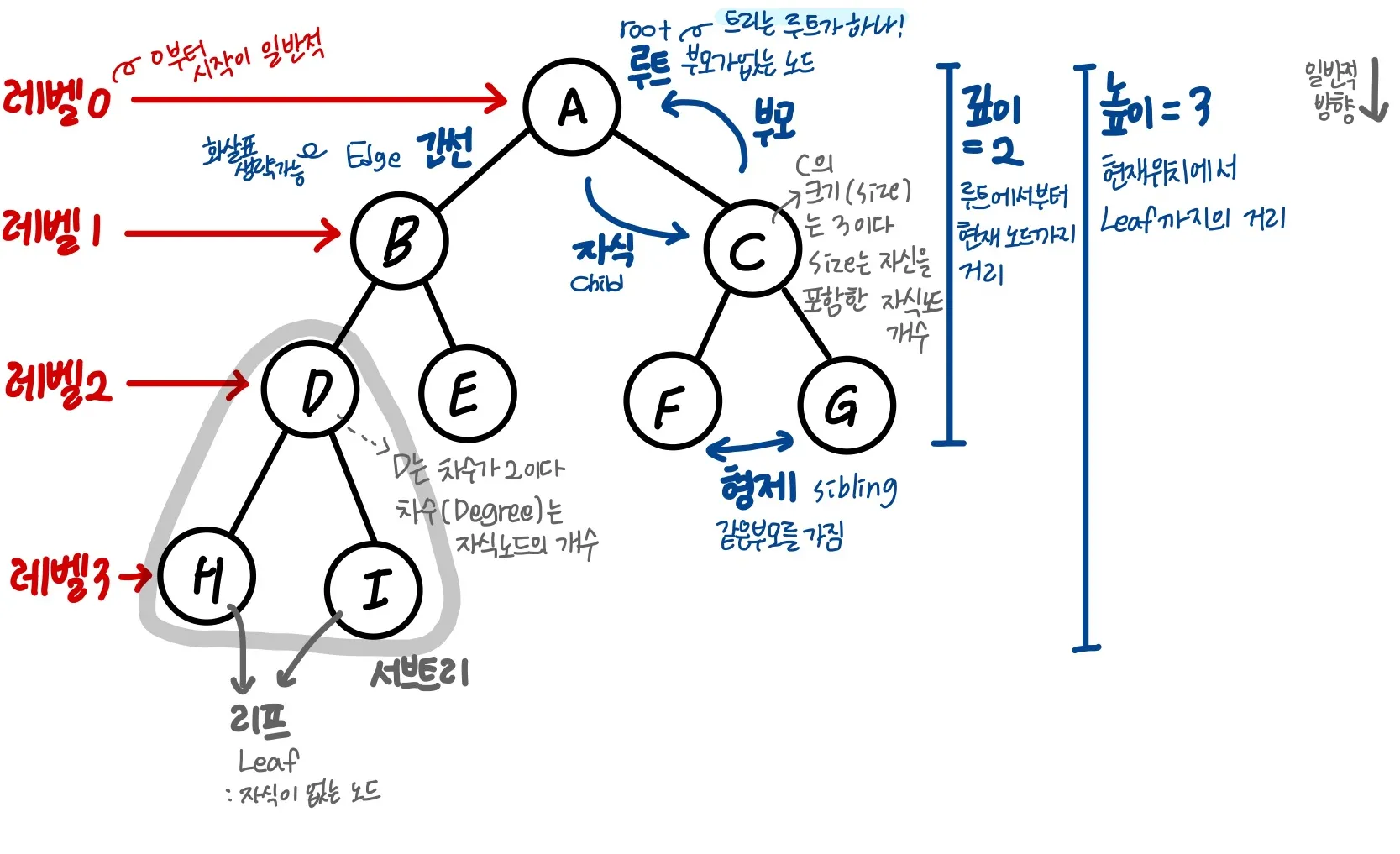
트리의 구성과 명칭
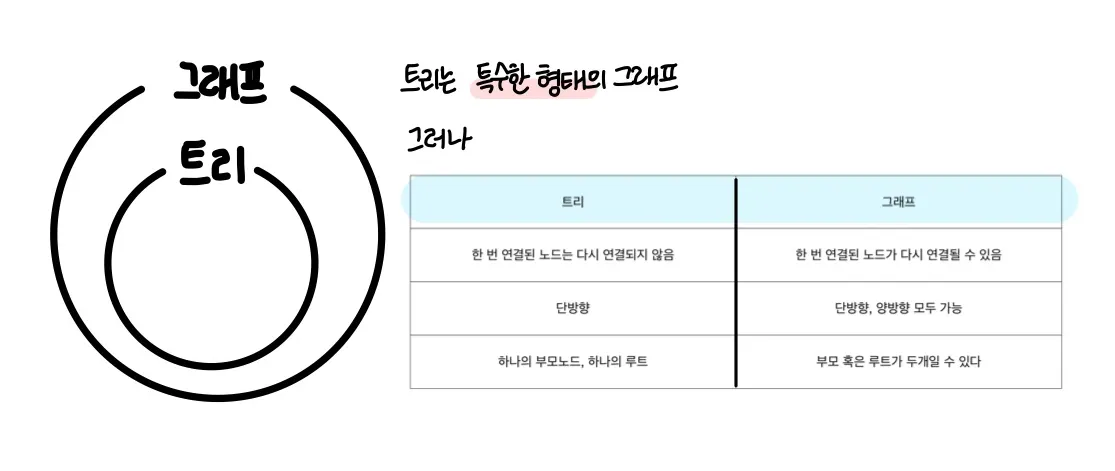
그래프 vs 트리
“트리는 순환 구조를 갖지 않는 그래프 입니다.”
그래프와 트리의 차이의 핵심은 순환구조(cyclic)가 아니라는 것이다
이진트리 Binary Trees
노드가 m개 이하의 자식을 갖고있는 트리 : m-ary tree (다항트리, 다진트리)
여기서 m=2이면, 즉 모든 노드의 차수가 2 이하이면 특별히 이진트리(Binary Tree)라고 하는 것
이진트리는 왼쪽, 오른쪽 최대 두개의 자식을 갖는 매우 단순한 형태
다진트리에 비해 훨씬 간결할 뿐 아닌 여러 알고리즘을 구현하는 일도 좀 더 간단하게 처리할 수 있어 보통 트리라 함은 이진트리를 일컫는다.
이진트리의 유형 Types of Binary Trees
1.
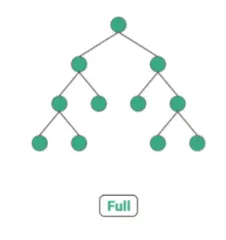
정 이진트리( Full Binary Tree ) : 모든 노드가 0개 혹은 2개의 자식 노드를 가짐
2.
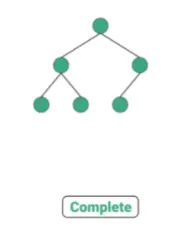
완전 이진 트리(Complete Binary Tree) : 마지막 레벨을 제외하고 모든 레벨이 완전히 채워져 있으며, 마지막 레벨의 모든 노드는 가장 왼쪽부터 채워져 있다.
3.
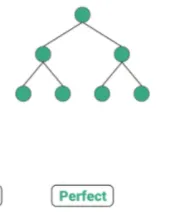
포화 이진 트리 ( Perfect Binary Tree ) : 모든 노드가 2개의 자식 노드를 갖고 있으며, 모든 리프 노드가 동일한 깊이 혹은 레벨을 갖는다. 문자 그대로, 가장 완벽한 유형의 트리다