힙 자료구조에 대한 정리
힙 정렬 설계(Heap Sort)
힙 정렬에서는 배열을 힙 구조로 재구성하는 makeheap()연산이 필요합니당
개선된 힙 생성 연산 MakeHeap 설계
미리 n개 레코드가 모두 주어진 경우에만 가능합니다.
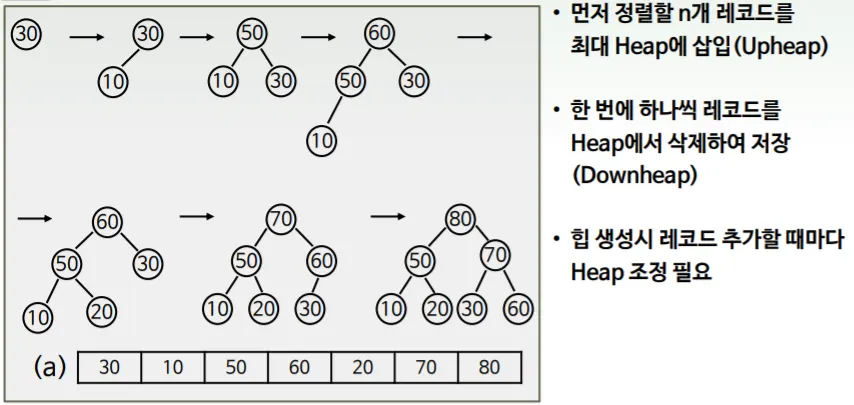
heap구현시 하나씩 삽입하면서 매번 Upheap연산을 수행해 주었다. 그것을 개선
루트부터 heap을 만들어가는 것이 아닌 leaf 노드부터 이미 heap들이 형성되어있다고 가정해 거꾸로 부모노드들을 붙여나가는 방식
1.
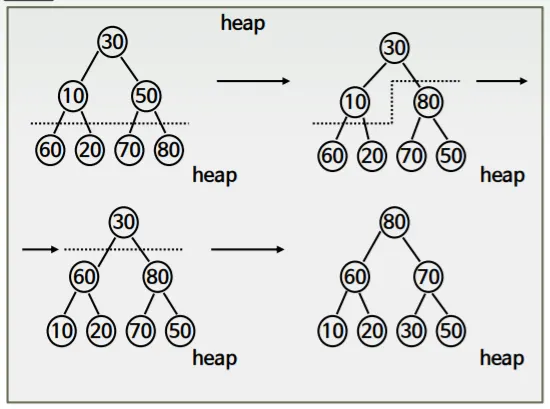
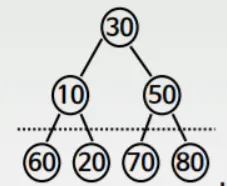
주어진 배열을 일단 heap으로 가정
2.
60, 20, 70, 80 은 자식노드가 없으므로 독립적인 maxheap으로 볼 수 있다.
3.
이제 그 위에 50까지를 보면, 인덱스에 의해 50이 부모노드, 70, 80이 자식노드가 되는데,
그럼 이제 60과 20은 여전히 독립적인 maxheap이고
50, 70, 80으로 이뤄진 heap은 힙 조정을 통해 80을 부모노드로 옮기고 70과 50을 자식노드로 갖도록 한다.
4.
이제 10까지를 보면,
10, 60, 20으로 이뤄진 힙, 80, 70, 50으로 이뤄진 힙 두개로 볼 수 있다.
10, 60, 20으로 이뤄진 힙 재조정
5.
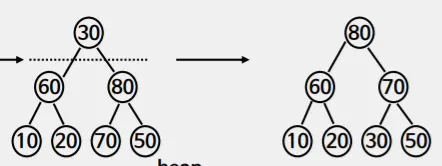
마지막으로 루트인 30까지 보고 힙조정을 다시 해주면
이렇게 완성!
힙정렬 구현
void MakeHeap(int A[], int Root, int LastNode)
{
int Parent, LeftSon, Son, RootValue;
Parent = Root;
RootValue = A[Root];
LeftSon = 2 * Parent + 1;
RightSon = LeftSon + 1;
while LeftSon <= LastNode {
if(RightSon <= LastNode && A[LeftSon] < A[RightSon])
Son = RightSon;
else Son = LeftSon; // LeftSon이랑 RightSon 중 키값이 더 큰 것을 Son에 저장
if (RootValue < A[Son]){
A[Parent] = A[Son]; // A[Son]이 RootValue보다 크면 A[Parent]와 A[son]을 바꾼다.(힙조정)
Parent = Son; // 이후에는 Parent 인덱스를 Son의 인덱스로 바꾸고
LeftSon = Parent * 2 + 1; // LeftSon과 RightSon 값도 다시 바꿔주고 아무튼 재조정하는 과정
RightSon = LeftSon + 1;}
else break;// A[Son]보다 RootValue가 크다면 조정할 필요가 없으므로 break
A[Parent] = RootValue;
}
C
복사
#define Swap(int &a, int &b) \
{\
int temp;\
temp = a;\
a = b;\
b = temp;\
}
void HeapSort(int A[], int n)
{/* 입력: A[0:n-1], n : 정렬할 원소 개수
출력: A[0:n-1] : 정렬된 배열 */
int i;
for(i=n/2;i>=0;i--)
MakeHeap(A, i, n-1);
for (i = n-1; i > 0; i--){
Swap(&A[0], &A[i]);
MakeHeap(A, 0, i-1); }
}
C
복사
성능 분석
•
제자리성 : 제자리 정렬
i, Parent, LeftSon, RightSon, Son, RootValue 등 상수크기의 메모리 사용
•
안정성 : 불안정
입력은 [80, 20, 50, 10, 50']이면
heap은 80 50' 50 10 20
정렬은 80 50' 50 20 10
될 수 있는 것
•
최악시간복잡도는
이미 반대로 정렬되어있는 입력의 경우이다.
그래도 항상 이하의 복잡도를 보장하므로 굉장히 성능이 좋은 정렬 방식이다.
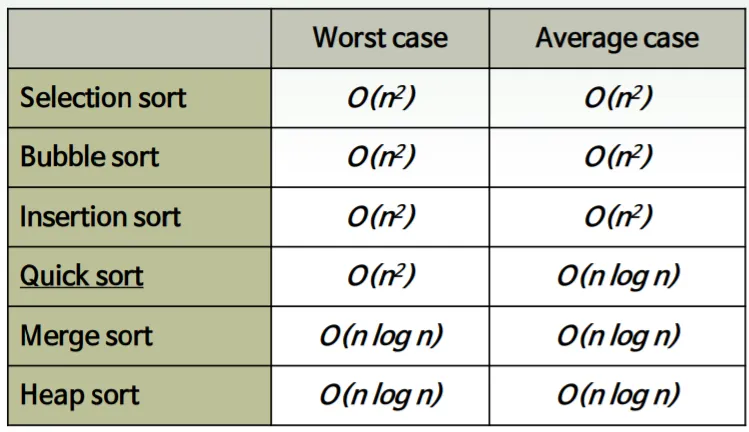
정렬알고리즘 시간복잡도 비교
계수정렬( Count Sort )
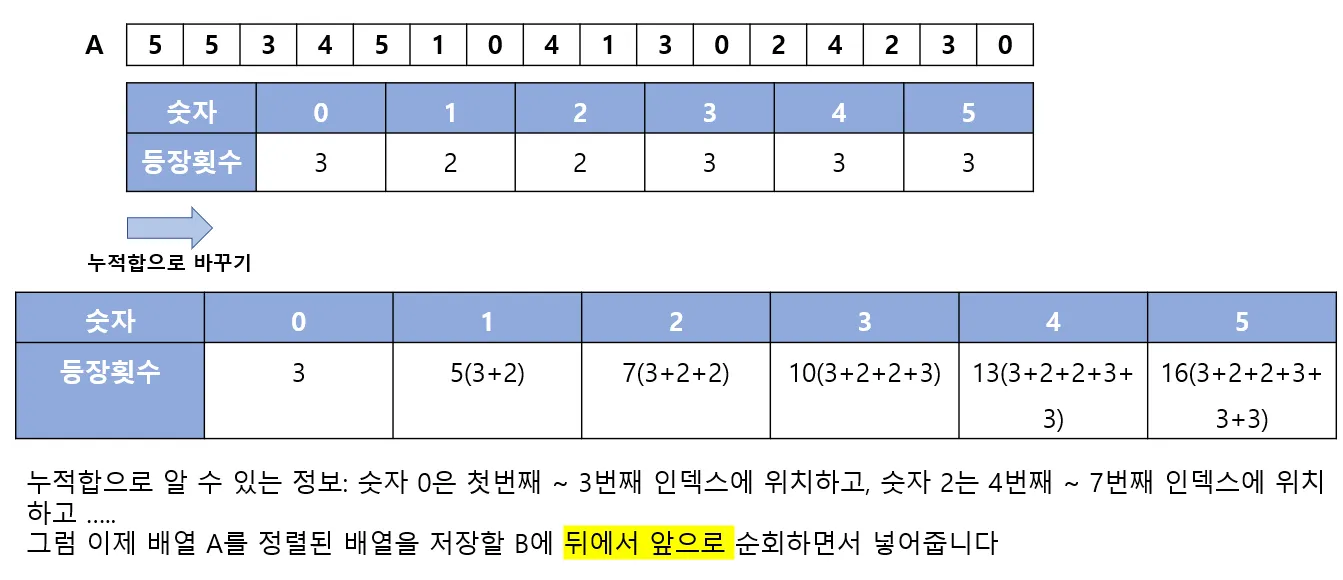
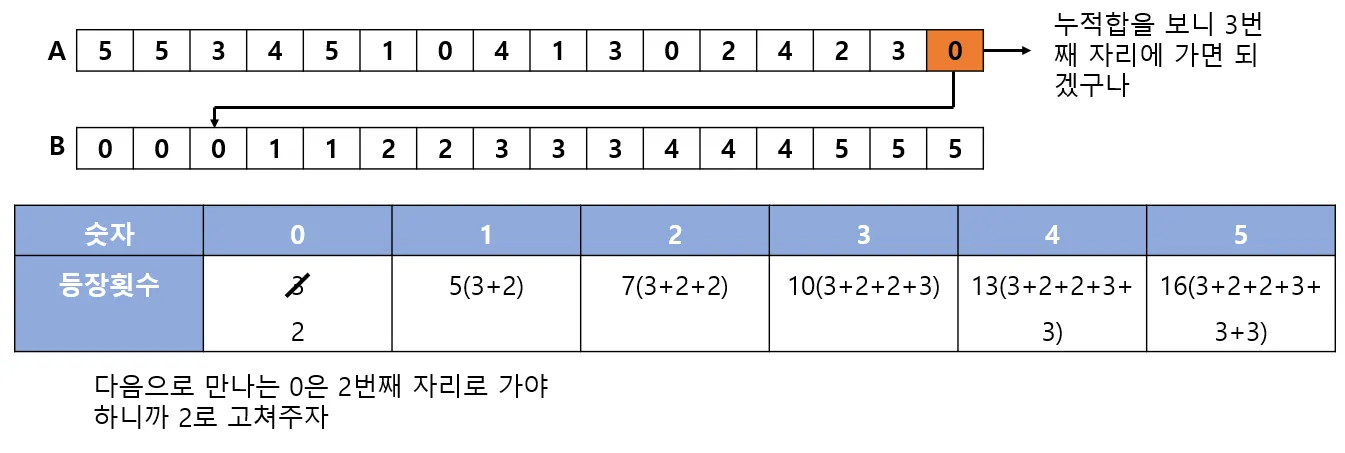
컴퓨터 과학에서 카운팅 정렬은 작은 양의 정수인 키에 따라 개체 컬렉션을 정렬하는 알고리즘입니다. 즉, 정수 정렬 알고리즘입니다. 고유한 키 값을 소유한 개체 수를 계산하고 해당 개수에 접두사 합계를 적용하여 출력 시퀀스에서 각 키 값의 위치를 결정하는 방식으로 작동합니다. 위키백과(영어)
[예시]
이런 방식을 반복
단점
•
0, 1, 1, 3, 3, 23, 32, 123, 43, 53 같은 배열의 경우 123이라는 압도적으로 큰 값 때문에 count 배열은 123의 크기를 가지지만 사실은 0, 1, 3, 23, 32, 43, 53 7개의 메모리만 사용한다. 엄청난 메모리 낭비가 된다.
⇒ 숫자가 커지면 메모리가 너무 커져서 사용할 수 없음
•
음수가 존재할 경우 사용할 수 없다
•
거의 쓸일이 없음.. 수능점수별 나열 같은 경우에 사용할 수 있다. 이런 경우에는 음수도 없고 0~100까지의 점수만을 요구하기 때문에 계수 정렬로 정렬하면 어렵지 않고 시간 복잡도 이득을 많이 볼 수 있다.
구현
CountSort (int A[ ], int n, int B[ ], int k ) {
/* 입력 : 정렬할 배열 A, 원소의 개수 n, 키의 범위 k
출력 : 정렬된 결과 배열 B */
{
for (i = 1; i <= k; i++) /*초기화*/
N[i] = 0; // 편의를 위해 인덱스 1부터 사용
for (j = 1; j <= n; j++) /*각 키의 개수*/
N[A[j]] = N[A[j]] + 1;
for (i = 2; i <= k; i++) /*키의 누적 합*/
N[i] = N[i] + N[i - 1];
for (i = n; j <= 1; j--) { /*정렬 결과를 배열 B에*/
B[N[A[j]]] = A[j];
N[A[j]] = N[A[j]] - 1;
}
}
C
복사
성능분석
•
비교정렬 아님
•
제자리성 : 제자리 정렬은 아님
입력크기에 비례하는 B[ ]가 사용됨
•
안정성 : 안정됨
순서대로 뒤쪽 레코드부터 가장 뒤쪽에 배치하게 된다.
•
count배열을 만드는 데 필요한 시간
•
sum 배열을 만드는데 필요한 시간
•
B배열(정렬된 배열) 채우는데 필요한 시간은 sum배열과 count배열의 합으로 볼 수 있으므로
•
평균 시간 복잡도 =
•
최악 시간 복잡도 =
단, k는 key값의 범위이다