Optimization

Neural Network 의 목적 : Loss function의 값을 최소화 시키는 파라미터 찾기 == 최적의 파라미터 찾기

최적의 파라미터를 찾는 문제를 푸는 것 == 최적화 ( Optimization )

깊은 네트워크 → 파라미터 매우 많음 → 파라미터 공간 매우 넓고 복잡 → 풀기 어려운 문제

최적의 파라미터 찾는 단서 → 미분값 → 파라미터에 대한 기울기를 구해 기울어진 방향으로 파라미터 값을 갱신하는 것을 반복하며 최적의 파라미터로 다가감 → 확률적 경사 하강법 ( SGD - Stochastic Gradient Descent )

SGD

SGD 수식

\bold{W} \leftarrow \bold{W}-\eta \frac{\partial L}{\partial \bold{W}}

\bold{W}

: 갱신할 파라미터

\frac{\partial L}{\partial \bold{W}}

\bold{W}

에 대한 Loss function의 기울기

\eta

: learning rate ( 학습률 ) 로, 보통 0.01이나 0.001같은 값을 미리 정해 사용한다

\leftarrow

: 우변의 값으로 좌변의 값을 갱신한다는 뜻

기울어진 방향으로 일정거리만 가겠다는 단순한 방법

[파이썬 수도 코드]

class SGD:
	def __init__(self, lr=0.01):
		self.lr = lr
	def update(self, params, grads):
		for key in params.keys():
			params[key] -= self.lr * grads[key]

model = ResNet50()
optimizer = SGD()
for epoch in range(num_epochs):
	for x, y in dataloader:
		grads = model.gradient(x, y)
		params = model.params
		optimizer.update(params, grads)
Python
복사

optimizer가 기울기와 파라미터 정보를 가지고 최적화를 수행하기 때문에 pytorch 같은 경우

import torch
model = ResNet50()
optimizer = torch.optim.SGD(model.parameters(), lr=initial_lr, momentum= ... )
Python
복사

tensor에 기울기가 저장되기 때문에 optimizer에 모델의 파라미터와 learning rate 등의 정보를 넘겨주면 optimizer.step()에서 업데이트를 해준다

SGD의 단점은 무엇일까

단순하고 구현이 쉬운 SGD. 단점은?

문제에 따라 비효율적일 때가 있다.

ex)

f(x, y)=\frac{1}{20}x^2 + y^2

이 함수는 기울기가 y=0으로 가까이 갈수록 작아니는 형태를 보인다

x축방향으로의 기울기는 상대적으로 작다

y축 방향 기울기는 가파르고 x축 방향 기울기는 작다

사실 이 식의 최솟값은 (0, 0)인 부분인데, 기울기들이 (0, 0)을 가리키고 있지는 않다.

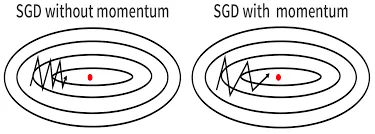
이 경우 SGD를 수행하면 지그재그로 이동하여 매우 비효율적이 된다.

이러한 비등방성 함수 ( anisotropy function ) ( 방향에 따라 성질이 달라지는 함수. 여기서는 기울기 이다 ) 에서는 SGD 사용시 탐색경로가 비효율적일 수 있다

→ 이 함수의 경우 기울어진 방향이 원래 최솟값과는 다른 방향을 가리켜서…

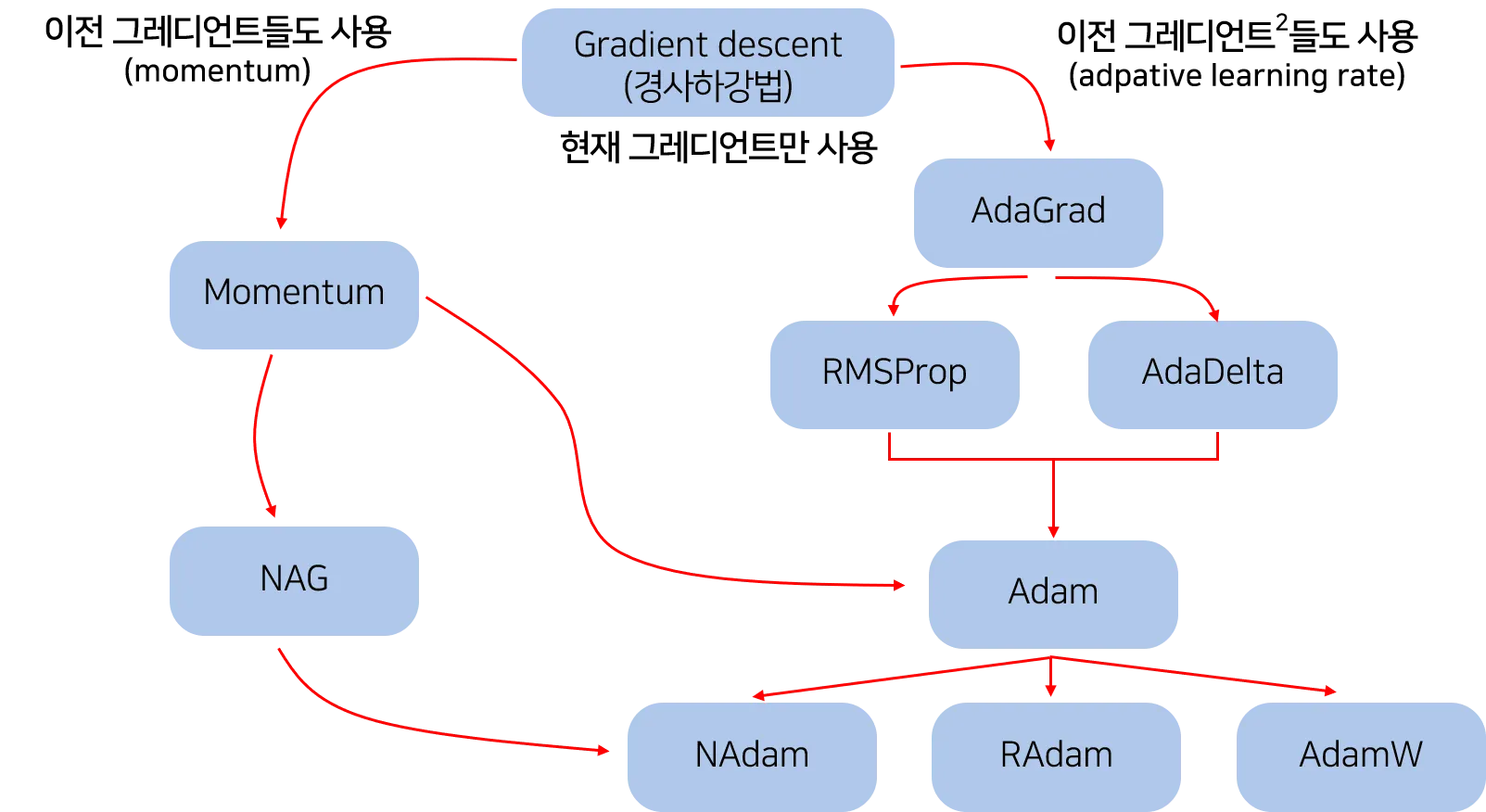
이를 개선한 것이 momentum, AdaGrad, Adam 등의 방법이다

momentum

momentum : 운동량

\bold{v}\leftarrow \alpha \bold{v}-\eta \frac{{\partial L}}{\partial \bold{W}}

\bold{W} \leftarrow\bold{W}+\bold{v}

\bold{v}

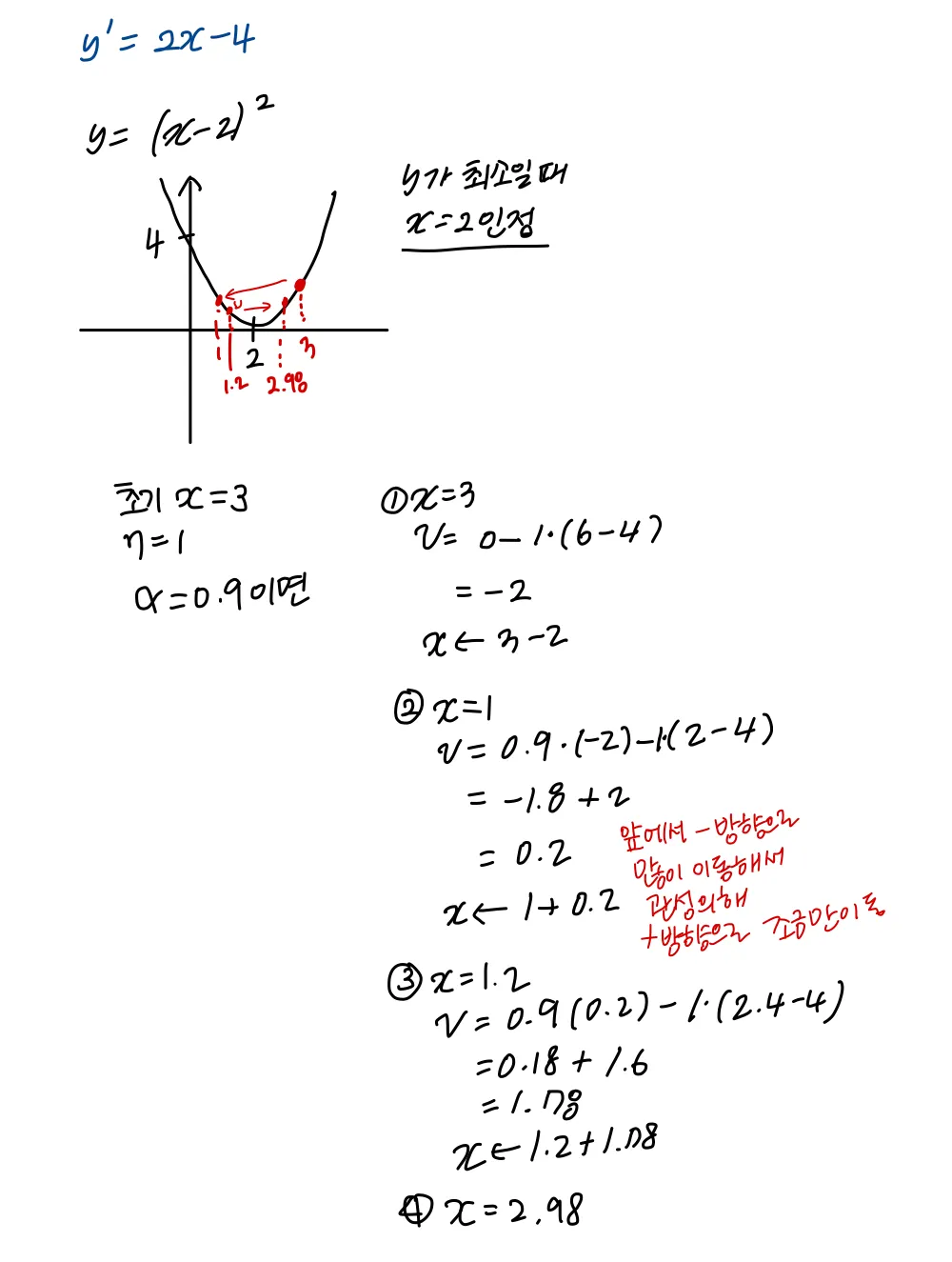
라는 변수가 새로 나왔다. 물리에서의 ‘속도'라고 할 수 있다.

첫번째 식은 기울기 방향으로 힘을 받아 물체가 가속된다 라고 할 수 있다.

momentum이 비교적 지그재그가 덜하다. x축 힘이 비교적 작지만 방향은 변하지 않아 한 방향으로 일정하게 가속하기 때문이다.

\alpha \bold{v}

항은 물체가 아무런 힘을 받지 않으면 서서히 하강시키는 역할이다. (

\alpha=0.9

등으로 설정)

이전 업데이트에서의 방향을 어느정도 반영하는 것으로 볼 수 있다.

class Momentum:
	def __init__(self, lr=0.01, momentum=0.9):
		self.lr, self.momentum, self.v = lr, momentum, None
	def update(self, params, grads:
		if self.v is None:
			self.v={}
			for key, val in params.items():
				self.v[key] = np.zeros_like(val) # 0으로 초기화
			
		for key in params.keys():
			self.v[keys] = self.momentum * self.v[key] - self.rl*grads[key]
			params[key] += self.v[key]
Python
복사

AdaGrad

Neural Network 학습은 learning rate

\eta

가 매우 중요하다

값이 너무 작으면 학습 시간이 너무 길어지고 / local minimum에 빠질 가능성이 높아지지만 너무 크면 발산해버려 학습이 되지 않을 수 있기 때문이다.

이를 해결하기 위한 효과적 방법이 learning rate decay(학습률 감소)이다.

말그대로 학습을 진행하면서 학습률을 점차 줄여가는 방식이다. 처음에는 크게, 점점 작게

가장 간단한 방법은 모든 파라미터의 학습률을 일괄적으로 줄이는 것일 것이다. 이를 더욱 발전시킨 것이 AdaGrad로, 각각의 파라미터에 맞춤형 learning rate 를 제공해준다.

개별 파라미터에 적응적(adaptive)으로 학습률을 조정하면서 학습을 진행한다

h\leftarrow h+\frac{\partial L}{\partial \bold{W}} \odot \frac{\partial L}{\partial \bold{W}}

\bold{W} \leftarrow \bold{W}+\eta \frac{1}{\sqrt{h}} \frac{\partial L}{\partial \bold{W}}

h는 보면 기존 기울기 값을 제곱해 계속 더해준다

\odot

: 행렬 원소별 곱셈 Hadamard product

그리고 파라미터 갱신시

\frac{1}{\sqrt{h}}

를 곱해 learning rate를 조정하는데, 이는 파라미터 중에 크게 갱신된 파라미터의 경우 learning rate를 작게한다는 것과 같다. 즉, learning rate의 감소가 파라미터마다 다르게 적용된다.

예를 들어 i번째 input 노드값이 a1,a2,a3,…ana_1, a_2 ,a_3, … a_na1​,a2​,a3​,…an​ 이고 파라미터들과 선형결합한 것이 w0+w1a1+w1a2+…+wnanw_0 + w_1 a_1 + w_1 a_2 + … + w_n a_nw0​+w1​a1​+w1​a2​+…+wn​an​ 인 경우 

a2가 sparse해 0인경우가 많다고 한다면, 많은 input에서  w0+0+w1a2+…+wnanw_0 + 0 + w_1 a_2 + … + w_n a_nw0​+0+w1​a2​+…+wn​an​ 이 되어 w2w_2w2​에 대한 편미분값도 0이된다. 즉, w2w_2w2​가 업데이트되지 않는다. 

그러다가 갑자기 0이 아닌 a2a_2a2​가 나와서 w2w_2w2​가 업데이트 된다면, 상대적으로 조금 업데이트 되어있는 상태이기 때문에 더 크게 업데이트 해줘야 수렴지점으로 빠르게 다가갈 수 있다. 

따라서 파라미터 업데이트 빈도 수에 따라 업데이트 크기를 다르게 해주는 것이다. 

AdaGrad는 h갱신에서 과거의 기울기를 제곱해 계속 더하기 때문에 학습이 진행될수록 learning rate가 작아질 수 밖에 없다. 그래서 학습을 길게하면 갱신량이 0이되어 전혀 갱신이 되지 않을 수 있다. 이를 개선한 것이 RMSProp으로, 과거 모든 기울기를 더하는 것이 아니라 먼 과거의 기울기는 서서히 잊고 새로운 기울기 정보를 크게 반영한다. 지수이동평균(Exponential Moving Average - EMA)를 사용한 방법이다. 과거 기울기 반영 규모를 기하급수적으로 감소시킨다.

class AdaGrad:
	def __init__(self, lr=0.1):
		self.lr = lr
		self.h=None
	def update(self, params, grads):
		if self.h is None:
			self.h = {}
			for key, val in params.items():
				self.h[key] = np.zeros+like(val) # 0으로 초기화
		
	for key, val in params.keys():
		self.h[key] += grads[key] * grads[key]
		params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key])  + 1e-7) # 분모 0방지
Python
복사

Adadelta

Adagrad에서는 iteration마다 learning rate가 작아지게 된다.

따라서 이를 해결하기 위해 크기

w

의 window를 사용한다 == 지난 모든 gradient정보가 아닌 이전의

w

개의 gradient정보만을 사용한다

또한 gradient의 제곱의 합이 아닌 gradient의 제곱에 대한 기댓값 (

E[g^2]_t

)을 저장한다

•

decaying average of squared gradients

E[g^2]_t = \gamma E[g^2]_{t-1} + (1-\gamma ) g_t^2

•

Δθt=−ηE[g2]t+ϵgt\Delta \theta_t = - \frac{\eta}{\sqrt{E[g^2]_t + \epsilon}}g_tΔθt​=−E[g2]t​+ϵ​η​gt​ 

•

RMS (Root mean square) = x12+x22+...+xn2n\sqrt{\frac{x_1^2 + x_2^2 + ... + x_n^2}{n}}nx12​+x22​+...+xn2​​​

\Delta \theta_t = - \frac{\eta}{RMS[g]_t}g_t

그런데 논문의 저자는 first-order method( 한번 미분한 변수로만 이루어진 식 )으로 파라미터를 업데이트 하면

\theta

와

\Delta \theta

의 단위(unit) 이 맞지 않는다고 했다

•

m단위의 fff 를 m/s 단위인 ▽tf\bigtriangledown_t f▽t​f 로 업데이트하면 안된다는 것이다

•

(ex) 함수 f의 단위 : unit(f)
정의역인 t의 단위 : unit(t)

◦

first order method : ddtf(t)∣t=t0  ≈  f(t)−f(t0)t−t0\frac{d}{dt} f(t)\mid_{t=t_0} \; \approx \; \frac{f(t)-f(t_0)}{t-t_0}dtd​f(t)∣t=t0​​≈t−t0​f(t)−f(t0​)​ 

◦

단위 : unit(f)unit(t)\frac{unit(f)}{unit(t)}unit(t)unit(f)​ 

◦

파라미터 업데이트 식 θt=θt−1+Δθ\theta_t=\theta_{t-1} + \Delta \thetaθt​=θt−1​+Δθ 에서  Δθ\Delta \thetaΔθ 가 g=▽θtJ(θt)g=\bigtriangledown_{\theta_t } J(\theta_t)g=▽θt​​J(θt​) 를 포함하기 때문에 

\Delta \theta \propto g \propto \frac{\partial J}{\partial \theta} \propto \frac{1}{unit \; of \; \theta}

마치 m단위를 변화시키는 데에 m/s를 사용하는 것과 유사하다

•

Δθ=−ηRMS[g]g\Delta \theta = -\frac{\eta}{RMS[g]} g Δθ=−RMS[g]η​g 에 second order method인 행렬인 헤시안 행렬을 도입해 unit을 맞춰준다

•

이정도로만 정리하도록 하겠다

•

결국 Δθt=−RMS[Δθ]t−1RMS[g]tgt\Delta \theta_t = -\frac{RMS[\Delta \theta]_{t-1}}{RMS[g]_t}g_tΔθt​=−RMS[g]t​RMS[Δθ]t−1​​gt​ , 최종 업데이트 식은 θt+1=θt+Δθt\theta_{t+1} = \theta_t + \Delta \theta_tθt+1​=θt​+Δθt​ 가 된다.

Adam (Adaptive Moment Estimation)

momentum + AdaGrad = Adam

decaying average of squared gradient 뿐 아니라 decaying average of gradients를 사용한다고 한다

•

Adam이름의 Moment는 momentum방식의 momentum의 의미 ( 관성 ) 와는 다르다

•

통계에서 자주 등장하는 용어로, 확률변수 XXX의 nnn차 moment를 E[Xn]E[X^n]E[Xn]으로 정의한다

•

1차 moment( 모평균 ) E[X]E[X]E[X] 

•

2차 moment E[X2]E[X^2]E[X2] 와 1차 moment로 모분산을 얻는다

•

E[X]E[X]E[X]와 E[X2]E[X^2]E[X2] 는 모수라 알 수 없는 값이므로 표본평균과 표본제곱의 평균으로 1,2차 moment를 추정한다 ( Estimation의 의미 )

•

mtm_tmt​ : gradient의 1차 moment에 대한 추정치
vtv_tvt​ : 2차 moment에 대한 추정치
이에 대한 가중평균 식
mt=β1mt−1+(1−β1)gtm_t = \beta_1 m_{t-1} + (1-\beta_1)g_tmt​=β1​mt−1​+(1−β1​)gt​
vt=β2vt−1+(1−β2)gt2v_t = \beta_2 v_{t-1} + (1-\beta_2)g_t^2vt​=β2​vt−1​+(1−β2​)gt2​

•

mtm_tmt​와 vtv_tvt​ 초기값은 0벡터로 주면 학습초기 가중치들이 0으로 편향되는 경향이 있어 (decay rate가 있거나 β1\beta_1β1​, β2\beta_2β2​ 가 1에 가까우면 심해짐 )
이를 완화시키기 위해 bias-corrected를 계산한다
mt^=mt1−β1t\hat{m_t} = \frac{m_t}{1-\beta_1^t}mt​^​=1−β1t​mt​​
vt^=vt1−β2t\hat{v_t}=\frac{v_t}{1-\beta_2^t}vt​^​=1−β2t​vt​​ 

•

최종업데이트 식은

\theta_{t+1} = \theta_t - \frac{\eta}{\sqrt{\hat{v_t}}+\epsilon} \hat{m_t}

\beta_1=0.9, \beta_2=0.999, \epsilon=10^{-8}

이 가장 보편적으로 쓰인다 (논문의 default 값)