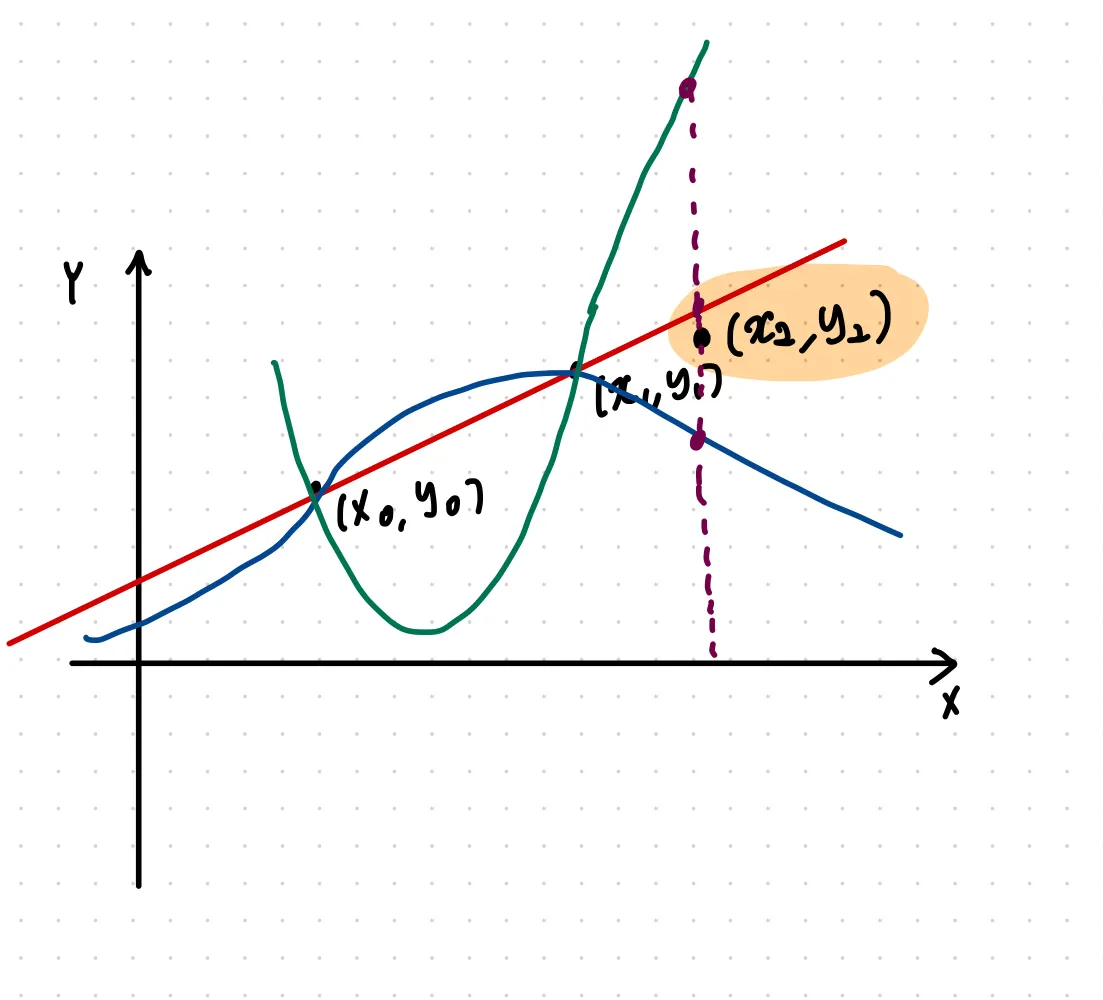CVPR 2022의 “A ConvNet for the 2020s” 논문 (링크) 을 보면, CNN은 그것의 inductive bias를 기반으로 좋은 성능을 보여왔다고 언급한다. 이에 대해서 자세히 알아보고자 한다.
inductive bias를 그대로 해석하면, “귀납적 편향”이다.
용어의 의미로부터 차근차근 이해해보자
Bias and Variance
머신러닝 / 딥러닝에서 bias와 variance는 무엇일까?
그림처럼 , , 를 정의해보자.
Bias
bias는 한마디로 예측값과 실제 정답과의 차이이다.
즉 예측값과 실제 정답이 얼마나 떨어져있는가를 나타낸다.
보통 다음 식에 절댓값을 취하거나 제곱을 하는 등으로 표현한다.
variance
variance는 다른 training dataset에 대해 예측값이 얼만큼 변화할 수 있느냐에 대한 Quantity의 개념이다. ( 양적인 개념 )
단순하게 생각하면 분산의 원래 의미처럼 예측값이 얼만큼 퍼져서 다양하게 출력될 수 있는지를 의미한다고 할 수 있다.
모델의 “flexibility”를 의미하기도 한다.
식은 원래 우리가 알고 있는 것과 같이 예측값의 평균과 예측값 ( 평균과 변량 ) 의 차이(편차)를 제곱해 나타낸 것이다.
bias와 variance의 관계
위의 그림은 bias 와 variance의 관계를 잘 나타낸 그림이다.
bias | variance | 특징 |
Low | Low | 예측값이 정답 근방에 분포 & 예측값이 특정 구간에 몰려있음 |
Low | High | 예측값이 정답 근방에 분포 & 예측값이 여러 곳으로 흩어져있음 |
High | Low | 예측값이 정답에서 떨어져있으나 & 예측값들이 한 곳에 몰려있음 |
High | High | 예측값이 정답에서 떨어져있고 & 예측값들이 서로 흩어져 있음 |
당연히 첫번째처럼 bias와 variance가 모두 낮은 것이 우리가 원하는 적합한 학습 결과일 것이다.
그러나
bias 와 variance의 Error식과의 관계를 살펴보면 이러한 결과는 얻기 어렵다는 것을 알 수 있다.
bias - variance Tradeoff
Error식은 위처럼 Bias와 Var로 분해된다.
[전개]
•
는 irreducible error라고 하여 근본적으로 줄일 수 없는 에러를 뜻하며, bias 와 variance를 0으로 만들더라도 그 모델이 완벽하다는 것을 의미하는 것은 아니기 때문에 추가된다.
•
bias와 variance가 클수록 error가 커진다
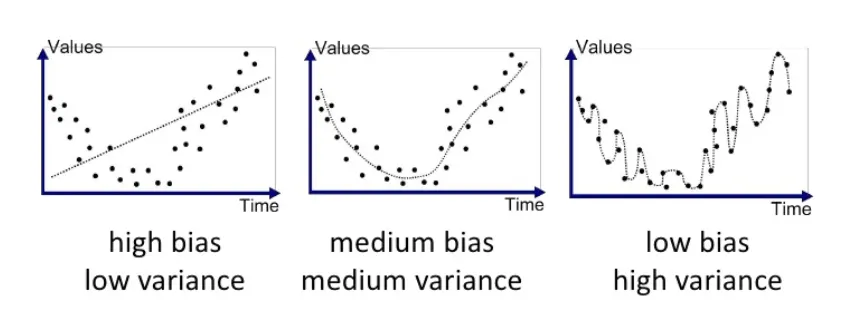
regression에서 bias 와 variance에 따른 예측값
검정색 점이 정답이고, 점선으로 표시된 선이 예측값의 regression이라고 할 때,
1.
high bias low variance : 예측값과 실제값이 많이 다르다. 그러나 예측값들의 편차가 작다 ( low variance )
⇒ 모델이 정답을 잘 예측하지 못하므로 underfitting 이라 할 수 있다.
⇒ 데이터 분포에 비해 모델이 너무 간단한 경우
2.
medium bias medium variance : high bias low variance에 비해 예측값과 정답값이 유사하지만 low bias high variance에 비하면 오차가 크다.
3.
low bias high variance : bias가 매우 작기에 예측값과 정답이 굉장히 유사하다. 그러나 예측값들의 편차가 매우 커졌다.(high variance )
⇒ training 데이터에 너무 맞춰진 overfitting이라 할 수 있다.
⇒ 모델의 복잡도가 데이터 분포보다 큰 경우
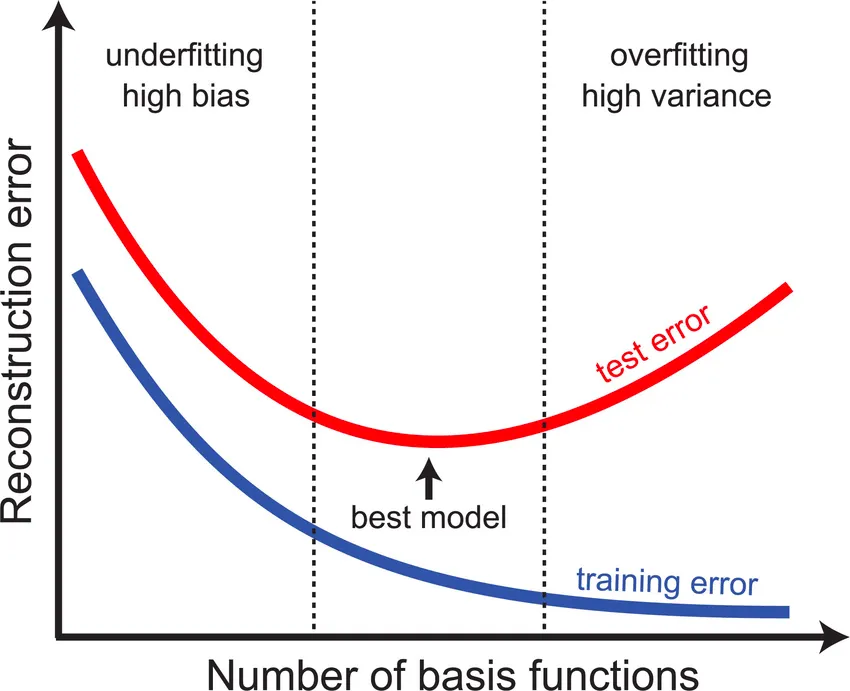
bias 와 variance는 서로 영향을 미치고 있다
bias를 줄이려 하면 overfitting에 가까워져 variance가 커지고
variance를 줄이려하면 underfitting에 가까워져 bias가 커진다.
적당한 수준의 bias와 variance를 갖는 수준까지 학습시키는 것이 중요하다.
⇒ 이를 찾는 가장 대표적인 방법이 validation set을 사용해 training error와 validation error가 함께 줄어들다가 갑자기 validation error가 증가하는 지점을 확인하는 것이다.
그렇다면 inductive bias(귀냡편향)는?
일단 귀납법에 대해서 생각해보자 (Inductive reasoning)
inductive reasoning
예시를 한번 들어보자. 시골에 놀러가서 방울 목걸이를 한 진돗개를 보게됐다. 그렇다면 나는 이곳의 진돗개들은 모두 방울 목걸이를 하고있구나! 라고 생각할 수 있다. 전형적인 유형의 귀납법이다.
사전적 정의에 따르면 개별적 특수한 사실이나 현상에서 그러한 사례가 포함되는 일반적인 결론을 이끌어내는 추론형식으로, 전제가 결론을 개연적으로 뒷받침하는 확률적 설명이다.
방울 목걸이를 한 진돗개라는 하나의 관찰이 가능한 일반적 가설 → “진돗개들은 모두 방울 목걸이를 하고 있다”
를 이끌어 낸 것이다.
ex ) 이 지역에는 진돗개가 있다. 진돗개가 아니더라도 모든 개는 방울 목걸이를 한다. 이 지역에는 다른 종류의 개는 없고 진돗개밖에 없다. 등등등…
⇒ 이것이 귀납법의 중요한 특징이다. 그리고 몇몇 가설은 틀릴 수 있다
이 가설들 중 가장 일반적이고 틀리지 않은 가설을 고르는 것은 매우 어렵다.
inductive reasoning in machine learning / deep learning
대부분의 머신러닝은 모든 데이터를 다 다룰 수 없고, (이 세상의 모든 데이터를 담는 것은 말이 안된다) 일부 데이터들만을 가지고 그를 기반으로 일반화된 모델을 만드는 것이 목적이다. → 처음 마주한 데이터에 대해서도 잘 예측하도록
“일부 sample만으로도 전체를 아우를 수 있는 일반적인 규칙을 모델링 하는 것 “
앞에서의 진돗개를 관찰하고 가설을 세우는 예시와 유사하다고 볼 수있다.
machine learning과 관련지어 생각하기 쉽도록 regression의 예시를 들어보자.
ex ) regression의 예시
그림처럼 두개의 점 (samples)가 주어졌을 때, 그려진 세개의 function들이 가설들이라고 할 수 있다. 여기서 우리의 목적은 이 function들 중 어떤 것이 맞는 가설일지 고르는 것이다.
새로운 sample 하나를 더 추가해보겠다.
새로운 sample의 정답과 가장 복잡한 함수와의 예측값이 가장 멀고, 가장 간단한 linear function과의 거리가 가장 가까워 보인다.
어디서 많이 본 것 같지 않은가? 앞에서 봤던 bias-variance tradeoff 문제와 유사하다.
이 경우 samples에 대한 사전지식을 기반으로 linear model를 선택할 수 있다.
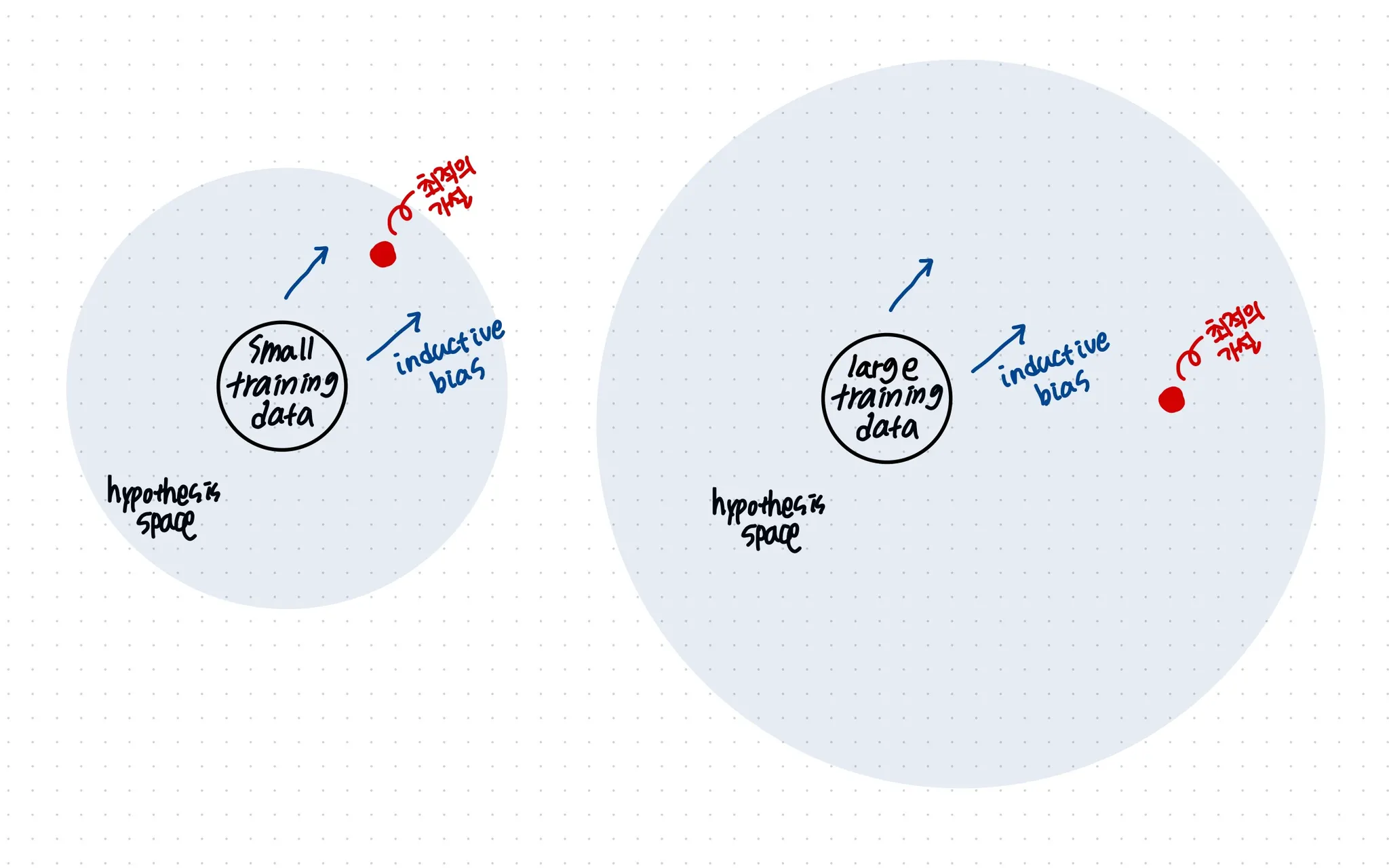
예시를 통해 알 수 있듯이, 모델에서 올바른 inductive bias를 선택한다면 모델을 더 잘 일반화시킬 수 있다. 특히 데이터가 적은 경우 강한 inductive bias가 모델을 더 잘 일반화 할 수 있게 해줄 것이다.
그러나 데이터가 풍부할 경우 더 많은 가설을 세울 수 있다는 것과 같으므로 inductive bias가 너무 크지 않도록 하는것이 더 좋을 수있다.
그림으로 보면 더 잘 이해할 수 있을 것이다.
그러나 대부분의 데이터는 small train data에 속할 것이기 때문에 inductive bias가 중요하게 여겨지는 듯 하다.
inductive bias는 머신러닝/딥러닝에서 다음과 같은 문제를 해결하기 위해 사용한다.
머신러닝/딥러닝 모델의 문제 1. brittle하다 : 데이터가 조금만 바뀌어도 모델의 결과가 망가진다
우리가 사용하는 데이터셋은 일종의 부분집합이라고 할 수 있고, 세상에는 무한하게 많은 데이터의 부분집합이 존재한다. 일부만 포함하는 데이터 셋으로 이 모든 데이터를 일반화하는 모델을 구성하는 것은 매우 어렵다
머신러닝/딥러닝 모델의 문제 2. Spurious하다 : 데이터 본연의 의미가 아닌 결과와 편향을 학습하게 된다. 겉으로 보기에만 괜찮아 보이도록 정답만 학습한다는 것이다.
이러한 문제는 사실 모두 일반화가 잘 안되는 문제 → train data를 벗어나지 못하는 문제라고 할 수 있다.
앞에서의 inductive reasoning의 예시와 좀 더 연결해보자면
Inductive bias는 개별적인 특수한 사실들 (train data내의 samples)을 기반으로 일반적인 결론 (일반화된 function / model)을 내기 위해 만약의 상황에 대한 추가적 가정이다.
일반화가 잘 된 모델들은 inductive bias의 한 유형을 갖게 된다.
inductive bias 의 예시
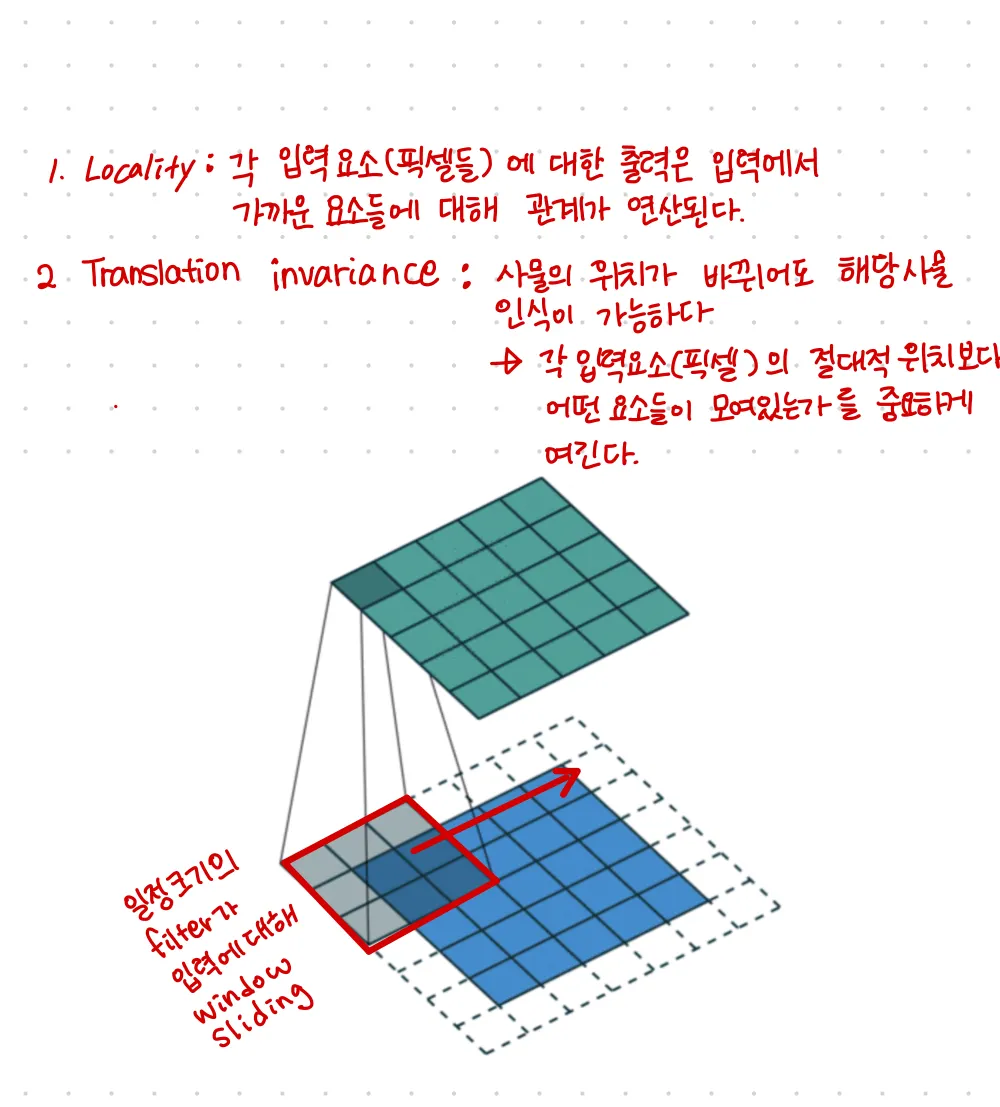
CNN의 inductive bias
딥러닝(CNN)에서는 Relational inductive bias(관계 귀납적 편향), hierarchical processing(계층적처리)를 제공한다.
이미지를 다루는 task들(classification, semantic segmentation, object detection 등) 에서 CNN의 성능이 좋은 이유가 바로 이것 때문이다.
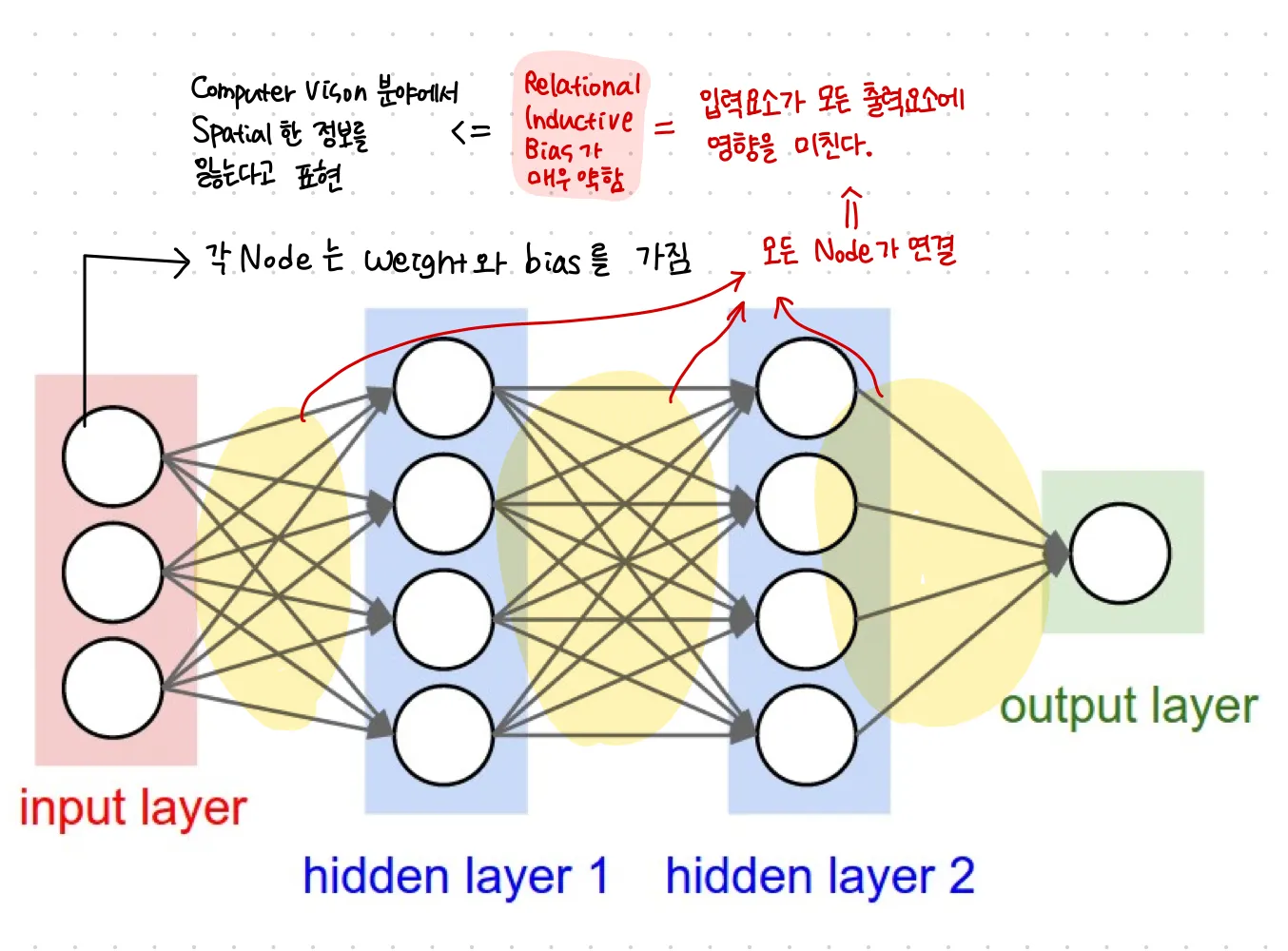
fully connected layer와의 비교
[ fully connected network ]
[ Convolutional neural network ]
추가적으로 RNN의 경우에는 공간의 개념이 아닌 시간의 개념이라는 것만 제외하면 CNN과 유사한 inductive bias를 갖는다. Sequential 과 Temporal invariance이다. 말그대로 Sequential은 입력이 시계열의 특징을 갖는다는 가정이며 Temporal invariance는 입력이 동일한 순서로 들어온다면 출력도 동일하다는 가정이다.
Transformer에는 Inductive Bias가 없을까?
CNN의 경우 이미지가 local한 영역에서 spatial한 정보를 얻을 것이 많다는 것을 가정한 모델이지만 Transformer는 positional embedding과 self attention을 사용하 전체적인 정보를 활용하기 때문에 지금까지의 내용으로 살펴봤을 때 Transformer는 CNN에 비해 Inductive bias가 부족하다고 할 수 있다. (그래서 dataset의 규모가 아주 클 때만 성능이 좋은 거라고 할 수 있을 것 같다)