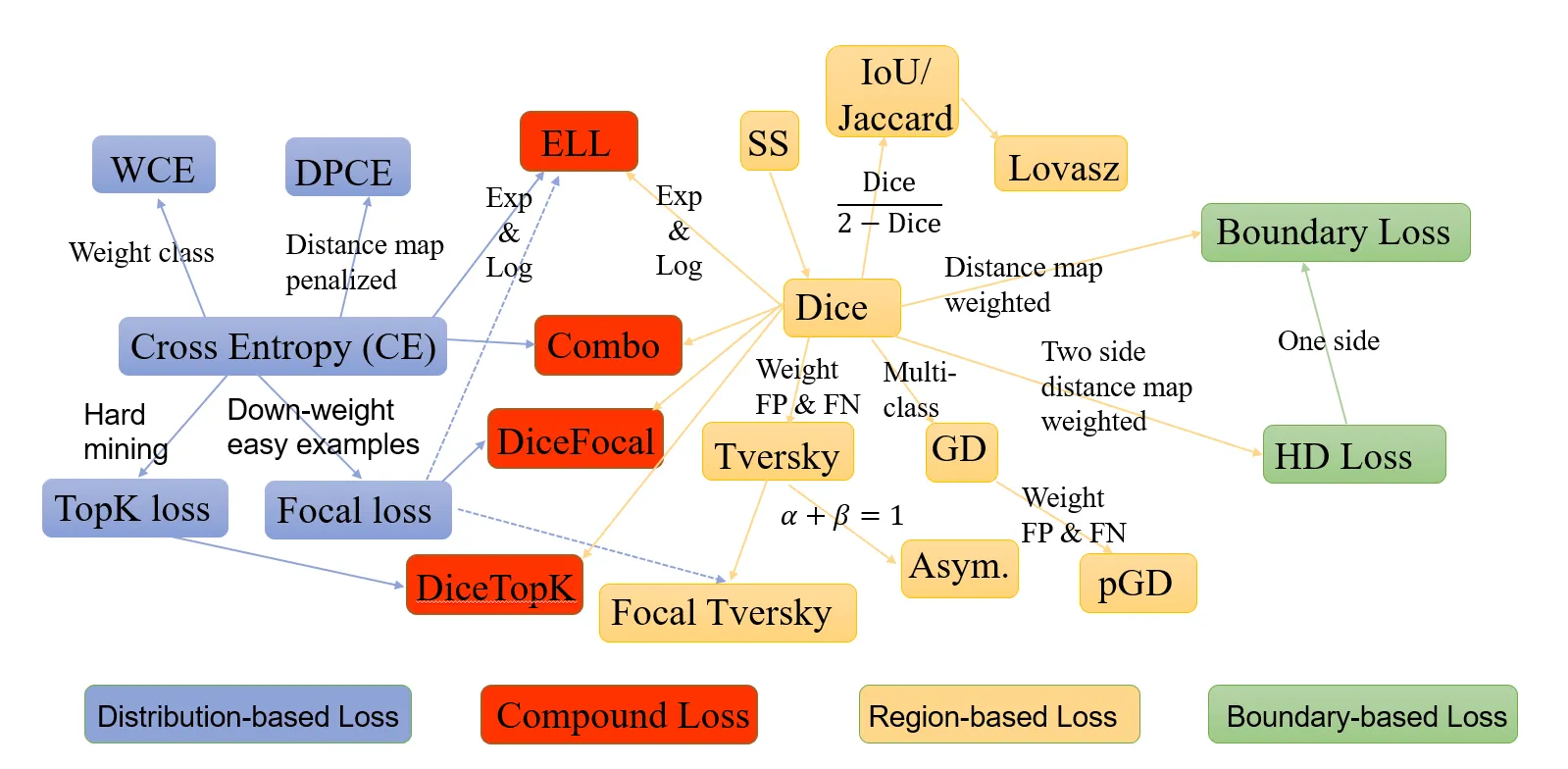
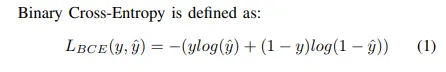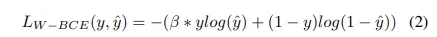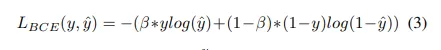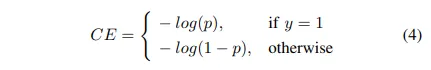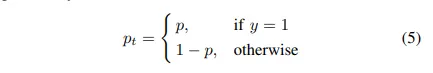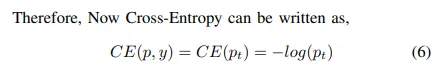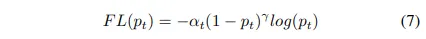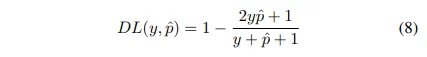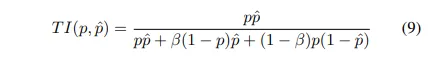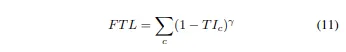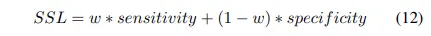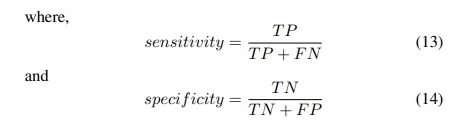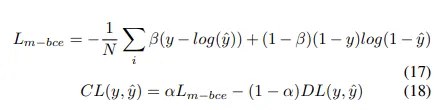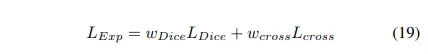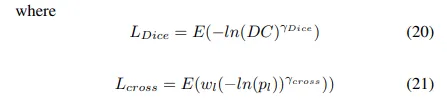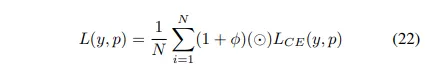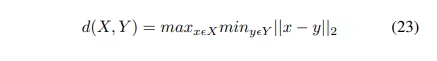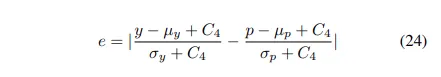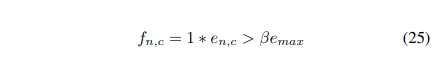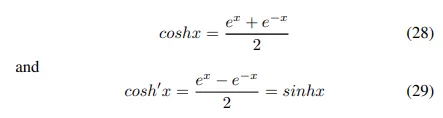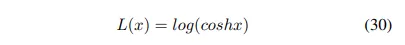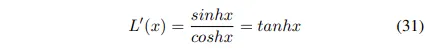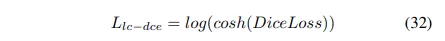[ Semantic Segmentation Loss 큰 분류 ]
•
Distribution-based loss
•
Region-based loss
•
Boundary-based loss
•
Compound loss
위 논문 참조
딥러닝 알고리즘은 objective를 최적화하고 배우기 위해 SGD를 사용
objective를 정확하고 빠르게 학습하려면 loss function이라고도 하는 objective에 대한 수학적 표현이 edge cases 까지 커버할 수 있는지 확인해야 한다.
손실 함수의 도입은 이러한 loss function이 라벨 분포에 기초하여 도출된 전통적인 기계 학습에 뿌리를 두고 있다.
예를 들어, BCE는 베르누이 분포에서 파생되고 Categorial Cross Entropy는 다항 분포(Multinoulli distribution)에서 파생된다. 본 논문에서, 우리는 Instance Segmentation 대신 semantic segmentation에 중점을 두었으므로 픽셀 수준의 클래스 수는 2개로 제한된다. 여기서는 널리 사용되는 15가지 손실 함수에 대해 살펴보고 사용 사례 시나리오를 이해할 것입니다.
Binary Cross Entropy
본래 Cross Entropy란 주어진 랜덤한 변수 혹은 사건의 집합의 두개의 probability distribution들의 차이의 측정으로 정의되었다. 이것은 classification objective로 널리 사용됐고, segmentation은 pixel level 에서의 classfication이므로 잘 작동하였다.
( 는 예측값)
Weighted Binary Cross Entropy(WCE)
a variant of binary cross entropy variant
이 경우 positive examples는 일부 coefficient 에 의해 가중치가 부여됩니다.
클래스가 두개이다보니, 0/1구분만 이뤄지므로 정답이 1일 경우에 가중치가 부여된다는 말
보통 skewed data에서 사용되어 클래스의 불균형 문제를 해결하기 위해 사용된다.
skewed data 예
Balanced Cross-Entorpy
WCE와 유사하다. 유일한 차이점은 positive examples만이 아니라 negative examples에도 가중치를 주는 것이다.
Focal Loss (FL)
이 또한 BCE의 변종이라 볼 수 있다
그것은 쉬운 사례의 기여도를 낮추고 모델이 어려운 사례를 배우는 데 더 집중할 수 있도록 한다.
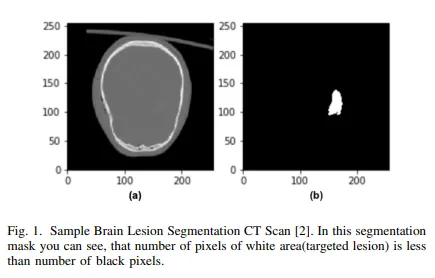
Fig 1과 같이 매우 불균형한 클래스 시나리오에 적합합니다. 이러한 FL이 어떻게 설계되는지 살펴보겠습니다. 우리는 먼저 BCE Loss를 살펴보고 Focal Loss이 CE서 어떻게 파생되는지 배울 것이다.
CE (라고 쓰여있지만 BCE)
편의를 위해 Focal Loss는 클래스에 대한 예측 확률을 다음과 같이 정의
그래서 CE를 다음과 같이 표현 가능하다
Focal Loss는 easy examples를 낮추고 modulating factor를 사용하여 hard negative에 training을 집중할 것을 제안한다.
modulating factor :
Dice Loss
Dice coefficient는 computer vision 계에서 metric으로 널리 사용된다
2016년 말, Dice Loss라는 이름으로 Loss에도 적용된다
1이 분자와 분모에 더해지면서 함수가 정의되지 않은 edge case scenario에 빠지지않도록 한다. 같은
Tversky Loss
Tversky index (TI)는 Dices coefficient의 일반화로 볼 수 있다. 이것은 FP(False Positive)와 FN(False Negative)에 weight를 더한다. 의 도움고 ㅏ함께
= 1/2 이면 regular Dice coefficient라고 할 수 있다. Dice Loss와 유사하게, Tversky Loss는 다음과 같이 정의된다.
Focal Tversky Loss
Focal Loss와 유사하게, common / easy ones에 downweighting 함으로써 어려운 example들에 집중한다.
Focal Tversky Loss 는 또한 의 도움으로 작은 ROI를 가진 것 등의 어려운 examples를 배운다
T1 : tversky indes
in range [1, 3]
Sensitivity Specificity Loss
Dice Coefficient와 유사하게 sensitivity와 specificity는 segmentation 예측 metric으로 널리 사용된다. 이 loss function에서, 우리는 우리는 w 매개 변수를 사용하여 클래스 불균형 문제를 해결할 수 있습니다.
sensitivity = Recall = 실제 P 중 P로 맞춘 비율
specificity = 실제 N 중 N으로 맞춘 비율
Shape-aware Loss
이름부터 shape를 고려한다는 의미이다
보통 모든 loss는 pixel level에서 작동하나, shape aware loss는 predicted segmentation의 곡선 주위의 점들 사이의 유클리드 거리를 곡선으로 만들기 위한 평균 점을 계산하고 cross entropy loss function를 위한 계수로 사용한다.
여기서 DL은 dice loss이다
Exponential Logarithmic Loss
이 loss는 덜 정확하게 예측된 구조들에 대해 집중한다. dice loss와 cross entropy loss가 함쳐진 식을 사용해서
Wong et al. 은 exponential and logarithmic transforms를 dice loss와 cross entropy에 적용해 더 정교한 decision boundaries와 정확한 data distribution이라는 이익을 포함하도록 하는 것을 제안했다
간단함을 위해 로 두었다
Distance map derived loss penalty term
Distance maps는 ground truth와 predicted map 사이의 euclidean이나 absolute같은 distance로 정의될 수 있다.
distance maps를 통합하는 방법은 segmentation과 함께 reconstruction head가 있는 NN아키텍처를 만들거나 loss function으로 유도하는 두 가지다.
같은 이론을 따라, Caliva et al.은 GT masks에서 나온 distance maps를 사용하고, loss function에 기반한 custom penalty를 생성했다.
이 접근을 통해, 네트워크를 segment하기 어려운 영역 경계에 집중하도록 가이드하는 것이 쉬워졌다
가 생성된 distance maps다
Note : 상수 1이 U-Net과 V-Net architectures에서의 vanishing gradient를 피하기 위해 추가된다
Hausdorff Distance Loss
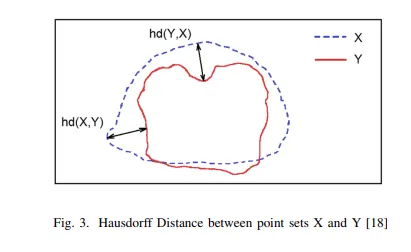
Hausdorff Distance( HD )는 segmentation에서 model의 성능을 추적하기 위한 metric으로 사용된다. 다음과 같이 정의됨
어떤 segmentation model이든 objective는 Hausdorff Distance를 최대화한다. 그러나 이것의 non-convex nature 때문에 loss function으로 널리 사용되지 않았다.
그러나 Karimi et al. 이 세가지 변종을 소개했다. HD라는 metric도 사용하고 loss function을 다루기 쉽게 하기 위해서.
이 세 가지 변형은
(i) 모든 HD 오류의 최대값을 취하기
(ii) 반경 r의 원형 구조를 배치하여 얻은 모든 오류의 최소값,
(iii) 누락된 세그먼트 픽셀 위에 배치된 컨볼루션 커널의 최대값 등
손실 함수의 일부로 HD를 사용할 수 있는 방법에 기초하여 설계되었다.
Correlation Maximized Structural Similarity Loss
많은 semantic segmentation loss function는 pixel level structural information는 무시한 채 classification error at pixel level에 초점을 맞춘다. 일부 다른 loss function는 CRF, GAN 등과 같은 구조적 우선 순위를 사용하여 정보를 추가하려고 시도했다.
이 손실 함수에서, zhao et al. [20]은 ground truth map와 predicted map 사이의 높은 양의 linear correlation을 달성하기 위해 a Structural Similarity Loss (SSL) 을 도입했다.
그것은 3단계로 나뉩니다.
1.
Structure Comparison
2.
Cross Entropy weight coefficient determination
3.
mini - batch loss definition
Structure comparison의 일환으로, 저자들은 ground truth와 prediction 사이의 linear correlation 정도를 측정할 수 있는 coefficient을 계산했다.
: stability factor (0.01 로 세팅 - 경험적으로 결정된 값)
: local mean and standard deviation of ground truth y
y는 local 영역의 중심에 존재하고 p는 예측 확률이다.
correlation 정도를 계산한 후, zhao et al. 은 cross entropy loss function을 위한 coefficient를 사용했다 이는 다음과 같이 정의된다.
위의 공식으로, loss function은 자동적으로 그들의 구조적 측면에의 correlation을 보여주지 않는 픽셀 단위 예측을 버린다.
Log-Cosh Dice Loss (논문의 제안)
Dice Coefficient는 (앞에서도 나오듯이) segmentation output을 평가하기 위해 널리 사용되는 metric
또한 segmentation objective의 수학적 표현을 충족시키기 때문에 loss function으로 사용하도록 수정되었다.
그러나 non-convex 특성 때문에 최적의 결과를 달성하지 못할 수 있다. Lovsz-Softmax loss[21]은 Lovsz 확장을 사용한 평활화를 추가하여 non-convex 손실 함수 문제를 해결하는 것을 목표로 했다.
Log-Cosh 접근법은 곡선을 평활하기 위한 회귀 기반 문제에 널리 사용되어 왔다.
Hyperbolic 함수는 tanh 레이어와 같은 비선형성의 관점에서 딥 러닝 커뮤니티에 의해 사용되어 왔다.
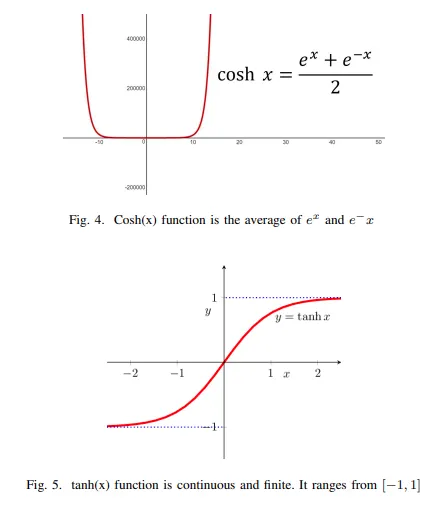
그들은 쉽게 구별할 수 있을 뿐만 아니라 다루기 쉽다. Cosh(x)는 (Fig 4)로 정의된다.
하지만 cosh(x)는 무한대로 가므로 범위를 제한해주기 위해서는 log space가 사용된다. → log-cosh function
chain rule을 사용하면
tanh는 [-1,1]의 범위를 갖기 떄문에 연속적이고 유한한 특성을 갖게 변한다
1차 미분 후 cosh함수의 log가 continuous이고 finite하다는 것을 보여준 위의 증명에 기초해서 우리는 dice coefficient의 특징을 캡슐화하면서 다루기 쉬운 특성으로 Log-Cosh Dice Loss 기능을 제안합니다.