프로그램 = 자료구조 + 알고리즘
ex) 최댓값 탐색 프로그램 = 배열 + 순차탐색
자료구조?
접근과 수정을 위해 데이터를 저장하고 정리하는 방법
ex. List, Stack, Queue, Tree, Graph
Correctness of Algorithm
알고리즘이 모든 input instance에 대해 correct output으로 중지되면 correct하다고 한다.
•
correct algorithm은 주어진 문제를 풀어낸다
•
incorrect algorithm은 완전히 중지되지 않거나 원했던 답이 아닌 다른 답으로 중지될 수 있다.
Efficiency of Algorithm
1.
Relative Efficiency
동일 목적 가진 알고리즘 A와 B의 실행시간, 메모리 사용량 등을 비교
2.
Absolute Efficiency
주어진 입력 크기에 대해 알고리즘 수행시간이 어떤 함수로 나타나는지 비교
효율적인 알고리즘 예
Greedy Method : 매 단계 가능한 해들 중 가장 좋은 해를 찾는 기법
최적해를 구하는 데에 사용되는 근사적인 방법으로, 여러 경우 중 하나를 결정해야 할 때마다 그 순간에 최적이라고 생각되는 것을 선택해 나가는 방식으로 진행하여 최종적인 해답에 도달한다. 순간마다 하는 선택은 그 순간에 대해 지역적으로는 최적이지만, 그 선택들을 계속 수집하여 최종적(전역적)인 해답을 만들었다고 해서, 그것이 최적이라는 보장은 없다. 하지만 탐욕알고리즘을 적용할 수 있는 문제들은 지역적으로 최적이면서 전역적으로 최적인 문제들이다.
탐욕 알고리즘이 잘 작동하는 문제는 대부분 탐욕스런 선택 조건(greedy choice property)과 최적 부분 구조 조건(optimal substructure)이라는 두 가지 조건이 만족된다. 탐욕스런 선택 조건은 앞의 선택이 이후의 선택에 영향을 주지 않는다는 것이며, 최적 부분 구조 조건은 문제에 대한 최적해가 부분문제에 대해서도 역시 최적해라는 것이다.
이러한 조건이 성립하지 않는 경우에는 탐욕 알고리즘은 최적해를 구하지 못한다. 하지만, 이러한 경우에도 탐욕 알고리즘은 근사 알고리즘으로 사용이 가능할 수 있으며, 대부분의 경우 계산 속도가 빠르기 때문에 실용적으로 사용할 수 있다. 이 경우 역시 어느 정도까지 최적해에 가까운 해를 구할 수 있는지를 보장하려면 엄밀한 증명이 필요하다.
어떤 특별한 구조가 있는 문제에 대해서는 탐욕 알고리즘이 언제나 최적해를 찾아낼 수 있다. 이 구조를 매트로이드라 한다. 매트로이드는 모든 문제에서 나타나는 것은 아니나, 여러 곳에서 발견되기 때문에 탐욕 알고리즘의 활용도를 높여 준다.
(예) 물건을 사고 거스름 돈을 동전으로만 받아야 하는 상황에서 가장 적은 수의 동전을 받을 수 있는 방법은? 동전은 500원, 100원, 50원, 10원이 사용된다
500원 → 100원 → 50원 → 10원 순으로 사용가능한 최대 동전수를 알아낸다
990원을 받야아한다면 1. 500원 1개가능 2. 990-500=490 100원 4개 가능 3. 490-400=90 50원 1개 가능 4. 90-50=40 10원 4개 가능
10개가 가장 적은 수의 동전을 사용하는 경우이다.
Divide and Conquer : 주어진 문제의 입력을 분할해 문제를 해결하는 기법
보통 재귀함수로 자연스럽게 구현된다
(예) 아주 많은 동전 더미 속 1개의 가짜 동전이 있다. 이 가짜 동전은 매우 정교해 누구도 눈으로 가짜인지 식별할 순 없지만 무게가 정상적인 동전보다 약간 가볍다. 1개의 양팔 저울만을 사용해 이 가짜 동전을 최소한의 저울질로 찾아낼 수 있는 방법은?
동전을 절반으로 나눠서 양팔저울에 놓으면 가짜동전 포함된 그룹이 더 가벼울 것
그렇게 계속 절반으로 나눠가며 비교하면 보다 효율적으로 찾을 수 있고
O(에 가까움
알고리즘적인 문제해결
1.
문제의 이해
2.
컴퓨팅 자원 확인
3.
적절한 자료구조 결정
4.
알고리즘 설계
5.
알고리즘 정당성 검증
6.
알고리즘 효율성 분석
7.
프로그램 작성
알고리즘 표현방법
1.
자연어 표현 (한국어 영어 등)
2.
흐름도 표현(flow chart)
3.
유사코드 표현(psedo code)
4.
프로그래밍 언어 표현
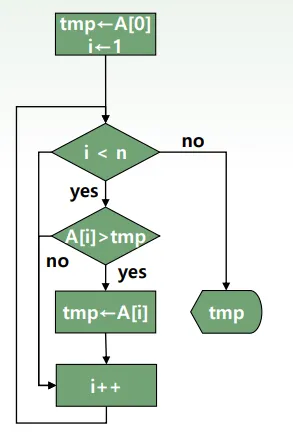
Q. 주어진 수들 중 최댓값 찾는 방법 표현
80, 90, 70, 30, 40, 20, 60, 10, 50
1.
자연어
가장 읽기 쉽지만 의미전달이 모호해질 수 있음
2.
흐름도
이해하기 쉽지만 알고리즘이 복잡하면 흐름도가 매우 복잡해지고 작성에도 많은 시간이 소요됨
3.
유사코드
고수준의 구조적 표현법이지만
프로그래밍 언어에 비해 덜 구체적이다( 구현상 세부 문제를 감춤으로써 알고리즘 핵심내용에 보다 집중하고자 할 경우 장점으로도 작용한다)
알고리즘 기술에 가장 많이 사용된다
4.
프로그래밍 언어
가장 정확하지만
구현 관련 세부사항들로 인해 알고리즘 핵심내용 파악에는 오히려 방해가 될 수 있다.
•
알고리즘 표현의 구체성 및 정확성
자연어 < 흐름도, 유사코드 < 프로그래밍 언어
•
알고리즘 표현속도
자연어 > 흐름도, 유사코드 > 프로그래밍 언어
알고리즘의 성능 분석
알고리즘의 성능 = 시간 측면 성능 + 공간 측면 성능
•
수행시간 분석
1.
두 개의 알고리즘의 실제 수행시간 측정
2.
실제로 구현하는 것이 필요
3.
동일 하드웨어 사용해야
•
알고리즘 복잡도 분석
1.
직접 구현 없이도 성능 분석 가능.
2.
알고리즘이 수행하는 연산 횟수를 측정
3.
일반적으로 연산 횟수는 n의 함수
4.
공간 복잡도 분석 : 수행시 필요로 하는 메모리 공간 분석
5.
시간 복잡도 분석 : 수행 시간 분석
수행시간 분석
주로 cloock함수 사용
clock ÷ 시간 으로 CLOCKS_PER_SEC을 통해 시간단위 환산
// clock(): time.h에 들어있는 함수로 프로그램에 의해 프로세서가 소비된 시간을 반환하는 함수입니다. 프로세서가 측정한 프로그램 실행시간이라 볼 수 있습니다.
// clock_t: clock ticks의 자료를 담고 있는 자료형으로 clock()의 반환형
#include <stdio.h>
#include <time.h> // time.h 헤더 파일을 include 해줘야합니다.
int main(){
clock_t start = clock(); // 시작 시간 저장
// 필요한 코드들 작성
clock_t end = clock(); // 코드가 끝난 시간 저장
// 걸린 시간 출력
// 단위: 초(second)
// CLOCKS_PER_SEC로 나눠줘야 초단위로 나옵니다.
printf("Time: %lf\n", (double)(end - start)/CLOCKS_PER_SEC);
return 0;
}
C
복사
예시
#include <stdio.h>
#include <time.h> // time.h 헤더 파일을 include 해줘야합니다.
#define ITERATION_TIME 100000
int main (){
clock_t start = clock(); // 시작 시간 저장
for(int i = 0; i < ITERATION_TIME; ++i){
for(int j = 0; j < ITERATION_TIME; ++j)
int do_something;
}
clock_t end = clock(); // 코드가 끝난 시간 저장
// 걸린 시간 출력
// 단위: 초(second)
// CLOCKS_PER_SEC로 나눠줘야 초단위로 나옵니다.
printf("Time: %lf\n",(double)(end - start)/CLOCKS_PER_SEC);
}
C
복사
< 공간 복잡도 분석 >
•
프로그램에 필요한 공간?
•
요소 두가지
1.
고정 공간 요구(fixed space requirements)
요구되는 프로그램 입력의 횟수/크기와 관계없는 공간
명령어 공간, 단순 변수, 고정 크기의 구조화 변수, 상수 등이 차지하는 공간
2.
가변 공간 요구(variable space requirements)
프로그램 입력(인스턴스 I)에 의존하는 공간
가변공간, 스택공간 등이 해당
c = fixed space requirements
= variable space requirements
ex) 고정공간요구
float abd(float a, float b, float c)
{
return a+b+b*c + (a+b-c) / (a+b) + 4.00;
}//세 개의 실수값을 입력으로 받아 어떠한 계산식의 결과를 리턴하는 함수
C
복사
입력에 따라 변하는 공간 없이 고정공간만을 가지게 된다.
즉,
ex) 가변공간요구
float rsum(float list[], int n)
{
if (n) return rsum(list, n-1) + list[n-1];
return 0;
}// n개의 요소를 가진 배열 list가 들어오면 원소들의 합을 리턴하는 함수
C
복사
n=3이면 rsum(list, 2) + list[2] = rsum(list, 1) + list[1] + list[2] = rsum(list, 0) + list[0] + list[1] + list[2] = list[0] + list[1] + list[2]
rsum이 순환호출된다.
컴파일러는 매개변수, 지역변수, 매 순환호출시의 복귀주소를 저장한다.
•
하나의 순환호출을 위해 요구되는 공간은
두개의 매개변수와 복귀 주소를 위해 필요한 바이트 수 =
Call-by-value, Call-by-ref 에 따른 차이
ex)
float sum(float list[], int n)
{
float tempsum = 0;
int i;
for (i=0;i<n;i++)
tempsum += list[i];
return tempsum;
}// 크기 n인 배열 list 내의 요소들의 합을 리턴하는 함수
C
복사
이 함수는 코드 실행 환경이 정해져 있지 않은 상황에서는 call-by-value이냐, call-by-ref이냐에 따라 가변공간요구, 고정공간요구가 달라질 수 있다.
•
Pascal의 경우 : call by value 형식
: 배열 전체가 임시 기억 장소에 복사된다.
•
C의 경우 : call by reference 형식
: 배열 첫 번째 요소의 주소가 전달된다.
call-by-value, call-by-reference
< 시간 복잡도 분석 >
프로그램 P 의해 소요되는 시간
ex)
: 각 연산을 수행하기 위해 필요한 상수시간
ADD(n), SUB(n), LDA(n), STA(n) : 특성n에 대한 연산 실행 횟수
그러나 연산 수행 횟수나, 걸리는 시간들을 정확하게 계산할 수가 없고, 특정 연산 횟수를 통해 어떤 프로그램이 더 낫다 라고 판단하기가 어렵기 때문에, Time step이라는 별도의 개념을 도입
입력 크기에 따른 program step(프로그램 단계) 수 변화를 통해 대략적인 분석을 한다
program step = 실행 시간이 인스턴스 특성에 구문적/의미적으로 독립성을 갖는 프로그램의 단위
한 단계 실행에 필요한 시간이 인스턴스 특성에 독립적이어야 한다.
ex)
a=2;
a=2*b+3*c/d-e+f/g/a/b/c;
// 한 라인당 한 step이라고 생각해도 무관하다
C
복사
(예시)
[n을 n번 더하는 문제]
각 알고리즘이 수행하는 연산의 개수를 세어보자(for 루프제어 연산 고려 x)
// 알고리즘A
sum <- n*n;
// 알고리즘 B
sum <- 0;
for i <- 1 to n do
sum <- sum + n
// 알고리즘 C
sum <- 0;
for i<-1 to n do
for j <- 1 to n do
sum <- sum+1;
C
복사
기본 보기
Search
간단한 알고리즘들이기 때문에 직관적으로 A가 제일 낫고, C가 제일 효율성이 떨어지는구나 라고 생각할 수 있지만, 각각의 연산에 얼마나 시간이 걸리는지 알 수가 없기 때문에 명확히 따지기 어려움
program step의 관점에서는 서로 다른 연산이더라도 동일한 하나의 step이라고 생각하고 전체 연산수를 계산한다.
따라서 전체 연산수는 program step의 관점에서 계산한 성능 비교라고 할 수 있겠다.
→ 알고리즘 A의 step수 2, 알고리즘 C의 step수 2*n*n+1 → A가 가장 효율적이고, C가 가장 비효율적이다