Probabilistic Model (확률모형)

*random variable : 확률 변수

확률 모형과 함께 등장하는 모수 추정, MLE, Log likelihood 등의 용어들을 정리해봅니다

확률모형이란

•

확률 모형은 수집된 / 관측된 데이터의 발생 확률 혹은 분포를 잘 근사하는 모형입니다.

•

Probabilistic model(확률모형), Statistical model(통계모형), Probability distribution(확률분포)

•

p(x∣θ),    p(x;θ),    pθ(x),    p(x)p(x|\theta), \;\; p(x;\theta), \;\;p_\theta(x), \;\; p(x)p(x∣θ),p(x;θ),pθ​(x),p(x)

•

θ\thetaθ 는 확률 모형을 정의하는 parameter(모수) 입니다. (descriptive measure 요약 통계량이기도 하다)

모수 추정

•

데이터의 이상적인 실제 확률 분포 (모집단의 분포) 가 p(x∣θ∗)p(x|\theta^*)p(x∣θ∗)이라면 이 분포 내에서 X를 수집한다고 이해할 수 있다.

•

모수를 추정한다 함은 p(x∣θ∗)p(x|\theta^*)p(x∣θ∗) 를 최대한 잘 근사하는 수학적 모형을 찾는 것이다. 

•

근사화된 모델을 사용하는 이유는 당연하게도 실제 데이터의 확률이나 실제 파라미터 θ∗\theta^*θ∗ 를 정확히 알 수는 없기 때문이다.

•

즉, 임의의 확률 모형 p(x)p(x)p(x)를 가정하고, 그 모형이 데이터를 잘 설명할 파라미터 θ\thetaθ 를 찾는 과정이 모수 추정이다.

•

만약 정규 분포를 가정했다면, p(x∣θ)=N(x∣μ,σ2),  θ=[μ,  σ]p(x|\theta) = N(x | \mu, \sigma^2), \; \theta = [\mu, \; \sigma]p(x∣θ)=N(x∣μ,σ2),θ=[μ,σ] 에서 θ\thetaθ의 값을 찾는 것이다. 

◦

여기서 θ\thetaθ 는 식에서 볼 수 있듯 평균과 표준편차이다.

◦

정규분포라는 가정 하에 최적의 평균과 표준편차 찾기

Maximum Likelihood Estimation (MLE)

그래서 모수추정을, 그니까 데이터를 잘 설명하는 모형을 어떻게 만드느냐

•

그 모형 안에서 관측된 데이터 X={x1,x2,x3,…,xn}X=\{x_1, x_2, x_3, …, x_n\}X={x1​,x2​,x3​,…,xn​} 의 발생확률이 전체적으로 최대로 만드는 것 

⇒ 이것이 MLE다.

\hat{\theta} = \underset{\theta}{\argmax}\;L(\theta)=\underset{\theta}{\argmax}\;p(X|\theta)

•

위의 L(θ)L(\theta)L(θ) 가 Likelihood function(가능도함수 or 우도 함수)로, 확률 모형을 나타내는 함수이다.

•

L(θ)L(\theta)L(θ) 는 X가 아닌 θ\thetaθ에 대한 함수임을 명심해야 한다. XXX는 고정되어 있는 데이터이며, θ\thetaθ가 변하면서 likelihood가 변하게 된다.

•

이 때 arg max⁡\argmaxargmax를 통해서 p(X∣θ)p(X|\theta)p(X∣θ)의 확률값이 최대가 되도록 하는 것이 목적이다. 

◦

주어진 θ\thetaθ에서 X의 발생확률을 최대로

•

독립항등분포 (iid;Independent and identically distributed random variables)를 가정하였을 때 전개

\hat{\theta} = \underset{\theta}{\argmax}\;L(\theta)=\underset{\theta}{\argmax}\;p(X|\theta)= \underset{\theta}{\argmax}\; \prod_{i=1}^n p(x_i|\theta)

정규분포라는 가정하에 직관적으로 살펴보기

•

앞에서 정규분포를 가정하였다면 평균과 표준편차가 θ\thetaθ라고 했다.

•

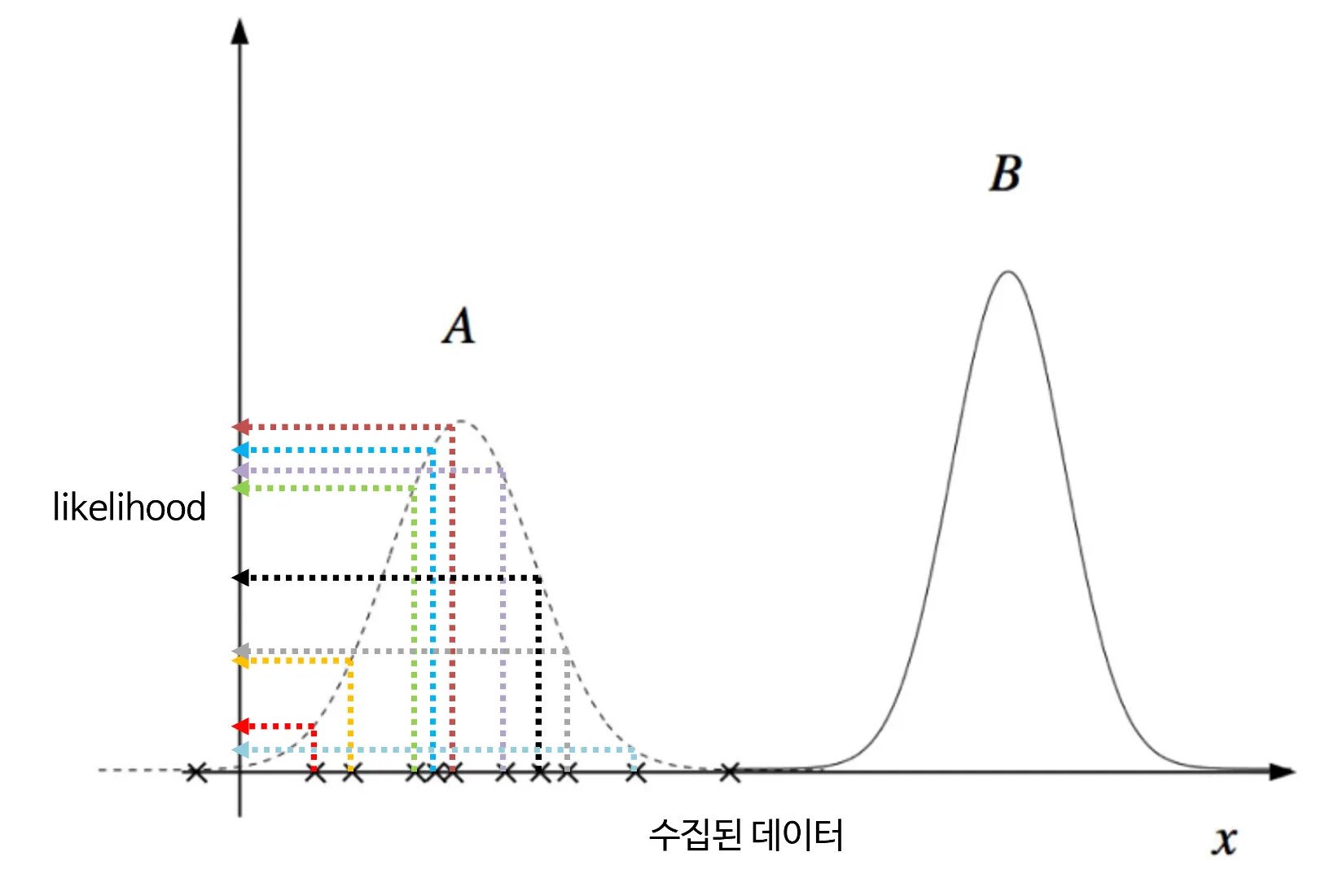
서로 다른 θ\thetaθ로 A와 B라는 분포가 있다면, 무엇이 데이터를 더 잘 표현하는 분포일까?

•

앞에서 iid를 가정하였기에 X의 likelihood를 연산하기 위해서는 각 데이터의 확률들을 모두 곱하면 된다.

•

B의 경우 0에 수렴하게 되고 A의 경우 비교적 높은 likelihood를 갖게된다.

Log likelihood function

•

likelihood에 log가 붙었다. 왜일까?

•

MSE 추정시 앞에서 보았던 것처럼 각 데이터의 likelihood를 모두 곱하였는데, 1보다 작은 수가 계속 곱해져 수가 매우 작아지므로, 합으로 표현하기 위해 log를 씌워준다.

•

l(x) = log(L(\theta))

\hat{\theta} = \underset{\theta}{\argmax}\;L(\theta)=\underset{\theta}{\argmax}\;l(x) = \underset{\theta}{\argmax}\; \log\prod_{i=1}^n p(x_i|\theta)=\underset{\theta}{\argmax}\; \sum_{i=1}^n \log p(x_i|\theta) = \underset{\theta}{\argmax}\;\frac{1}{n}\sum_{i=1}^n\log p(x_i|\theta)

•

log는 증가함수기에  arg max⁡θ  L(θ)=arg max⁡θ  l(x)\underset{\theta}{\argmax}\;L(\theta)=\underset{\theta}{\argmax}\;l(x)θargmax​L(θ)=θargmax​l(x)

◦

 (최댓값에 해당하는 θ\thetaθ를 구하는 데에는 영향이 없음)

•

합을 최대로 만드는 \theta를 구하는 것과 평균을 최대로 만드는 \theta를 구하는 것은 동일하므로 arg max⁡θ  ∑i=1nlog⁡p(xi∣θ)=arg max⁡θ  1n∑i=1nlog⁡p(xi∣θ)\underset{\theta}{\argmax}\; \sum_{i=1}^n \log p(x_i|\theta) = \underset{\theta}{\argmax}\;\frac{1}{n}\sum_{i=1}^n\log p(x_i|\theta)θargmax​∑i=1n​logp(xi​∣θ)=θargmax​n1​∑i=1n​logp(xi​∣θ) 

•

최종적으로 전개된 마지막 식을 empirical expectation이라고 부른다.

E_{x~p(x|\theta^*)}\log p(x_i|\theta)\approx \frac{1}{n}\sum_{i=1}^n\log p(x_i|\theta)