힙은 최댓값 및 최솟값을 찾아내는 연산을 빠르게 하기 위해 고안된 완전이진트리를 기본으로 한 자료구조로서 다음과 같은 힙 속성을 만족한다. A가 B의 부모노드 이면, A의 키값과 B의 키값 사이에는 대소관계가 성립한다. 위키백과
•
우선순위 큐를 위해 만들어진 자료구조다
•
우선순위 큐:
◦
큐에 우선순위를 도입한 자료구조. 우선순위가 높은 데이터부터 삭제된다. (먼저 나간다)
◦
배열, 연결리스트, 힙으로 구현 가능. 힙이 가장 효율적
•
최댓값/최솟값을 빠르게 찾아내도록 만들어졌다.
•
힙 트리는 중복 값을 허용한다
종류
•
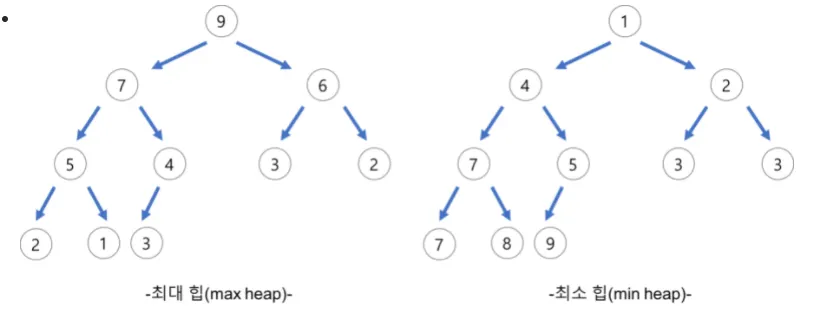
최대 힙(max heap)
부모노드 키 값 ≥ 자식노드 키값
•
최소 힙(min heap)
부모노드 키 값 ≤ 자식노드 키값
구현
•
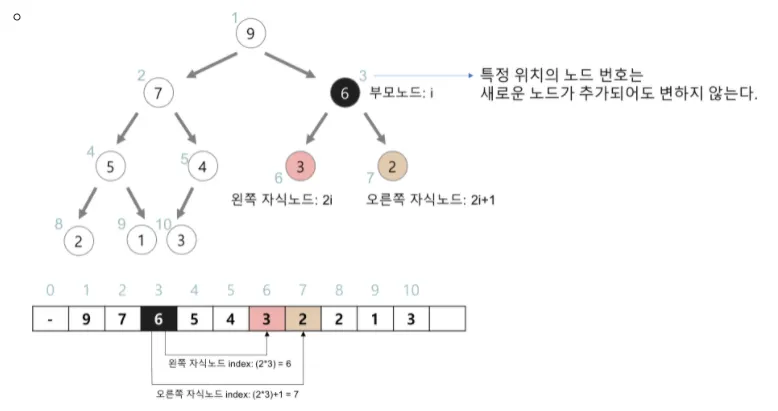
완전이진트리이기 때문에 각 노드에 인덱스를 부여해 배열로 구현이 가능하다.
•
편의를 위해 0인덱스는 사용하지 않는다.
•
특정 위치의 노드 인덱스는 새로운 노드가 추가되더라도 변하지 않는다. ex) 루트노드의 오른쪽 노드 번호는 항상 3
왼쪽 자식의 인덱스 = 부모 인덱스 * 2
오른쪽 자식의 인덱스 = 부모 인덱스 * 2 + 1
부모의 인덱스 = 자식의 인덱스 / 2 (몫)
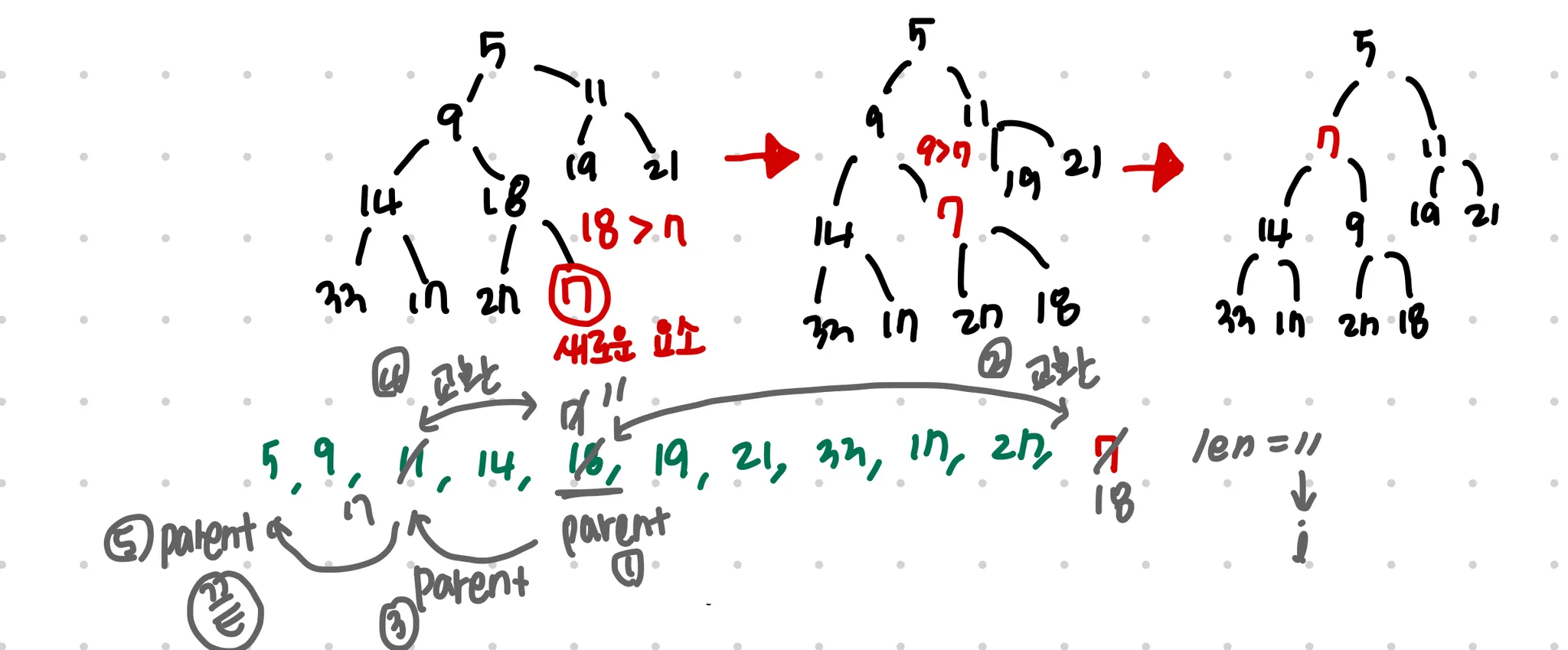
heap의 삽입(Upheap 연산)
1.
요소를 가장 하위 레벨의 최대한 왼쪽으로 삽입 ( 배열에선 가장 마지막)
2.
부모값과 비교해 더 작은 경우 위치 변경 (위치 변경이 없을 때 까지 반복)
시간복잡도 :
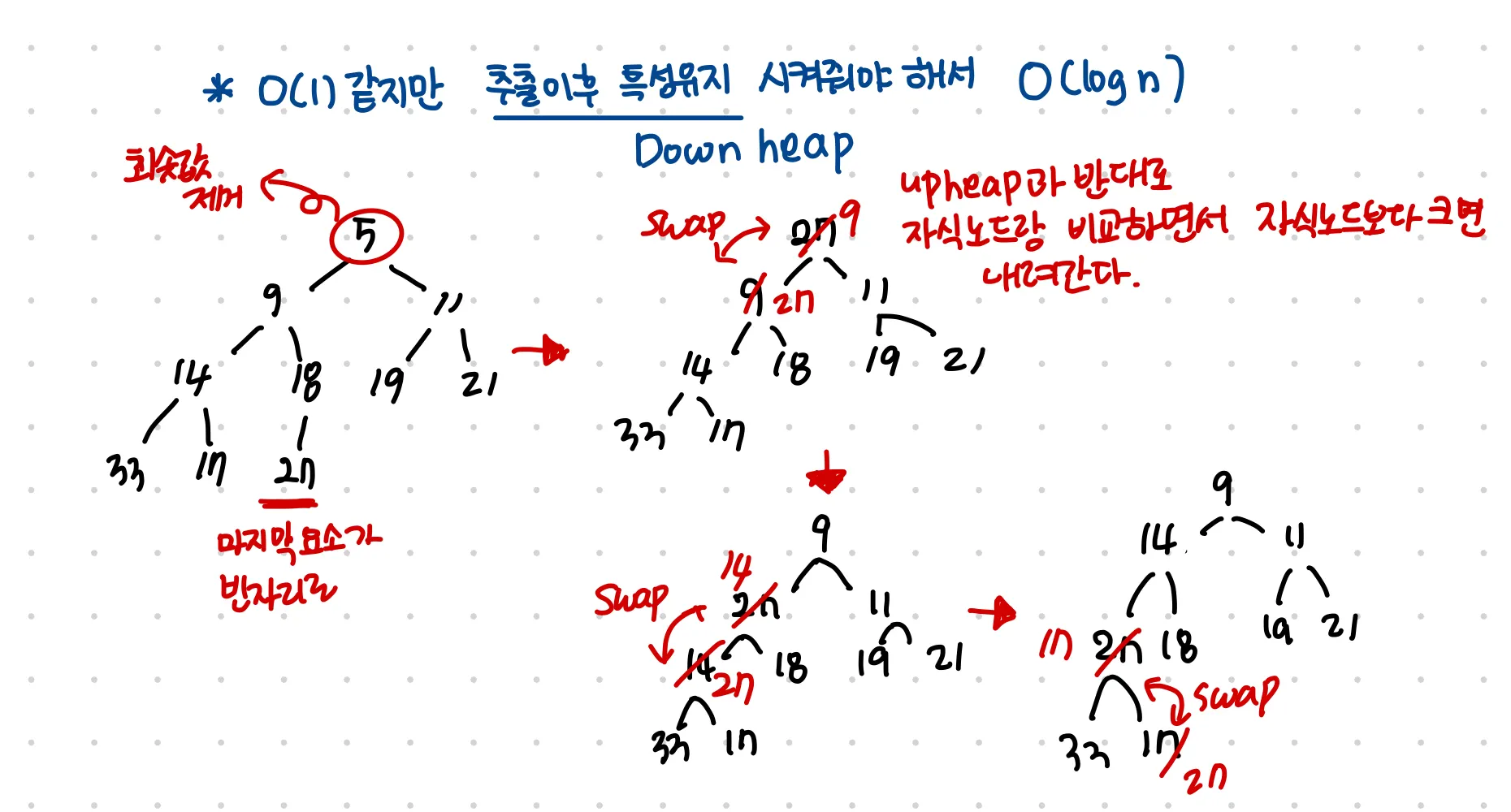
heap의 삭제(Downheap 연산)
•
시간복잡도
구현
# 최소힙
class BinaryHeap():
def __init__(self):
self.items = [None]
def __len__(self):
return len(self.items) - 1
def insert(self, k):
self.items.append(k)
self._percolate_up()
def _percolate_up(self):
i = len(self)
parent = i//2
while parent >= 0:
# 부모와 비교하여 더 작으면 둘을 교환
if self.items[i] < self.items[parent]:
self.items[parent], self.items[i] = self.items[i], self.items[parent]
i = parent
parent = i // 2
def extract(self):
extracted = self.items[1]
self.items[1] = self.items[len(self)]
self.items.pop()
self._percolate_down(1)
return extracted
def _percolate_down(self, idx):
left = idx * 2
right = idx * 2 + 1
smallest = idx
if left <= len(self) and self.items[left] < self.items[smallest]:
# 왼 노드로 지정된 index가 힙 요소 길이를 벗어나지 않고 현재 smallest의 값보다 작을경우
smallest= left # smallest는 left(왼노드의 인덱스)로 교환
if right <= len(self) and self.items[right] < self.items[smallest]:
smallest = right # right에 대해 동일하게
if smallest != idx:
# 자식노드들과의 비교가 끝났을 때 smallest가 입력된 idx와 다르다면 둘을 교체
self.items[idx], self.items[smallest] = self.items[smallest], self.items[idx]
self._percolate_down(smallest) # 교체 하였으므로 smallest위치에는 원래 idx에 있던 값이 존재함. 이에 대해서 다시 재귀 호출. 점점 내려가는 과정을 이렇게 구현
Python
복사