Search

[작성중]Subspace의 basis와 dimension

Subspace (부분 공간)

subspace HH는 선형결합에 닫혀있는 (closed under linear combination) Rn\mathbb{R}^n의 subset이다.

선형결합에 닫혀있다 라는 것은…

•
“subspace내의 n차원 벡터들끼리 선형 결합 연산이 성립하면서 그 결과 또한 그 공간에 속한다”는 의미이다.
•
그렇기에 zero vector를 무조건 포함해야 한다.
•
Span은 주어진 벡터들의 가능한 모든 선형결합에 대한 결과 벡터들을 하나의 공간에 몰아넣은 것이기 때문에 무조건 선형 결합에 닫혀있고, 따라서 언제나 subspace이다. → 따라서 span과 subspace를 거의 비슷한 개념으로 이해하여도 좋다.

Basis (기저) of a Subspace

a basis of a subspace H는 다음 두 조건을 만족하는 벡터들의 집합이다. 1. 주어진 subspace H를 완전히 span한다. 2. 선형 독립이다.
예시 1)
[100],[010],[001]\begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix}, \begin{bmatrix} 0 \\ 1 \\ 0 \end{bmatrix}, \begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix}
•
이 벡터들의 조합으로 R3\mathbb{R}^3전체를 span할 수 있다.
•
세 벡터는 선형 독립이다.
⇒ 이 벡터 집합은 R3\mathbb{R}^3의 basis이다.
예시 2)
subspace H=Span(v1,v2,v3)H = Span(\bold{v}_1, \bold{v}_2, \bold{v}_3) 에서 v1\bold{v}_1과 v2\bold{v}_2는 선형 독립으로, Span(v1,v2)Span(\bold{v}_1, \bold{v}_2)가 plane을 형성하고, v3=2v1+3v2\bold{v}_3 = 2\bold{v}_1 + 3\bold{v}_2일 때
•
v3\bold{v}_3은 Span(v1,v2)Span(\bold{v}_1, \bold{v}_2)에 속하므로 Span(v1,v2)Span(\bold{v}_1, \bold{v}_2)는 Span(v1,v2,v3)Span(\bold{v}_1, \bold{v}_2, \bold{v}_3) 과 같다.
•
따라서 {v1,v2}\{ \bold{v}_1, \bold{v}_2 \}는 HH의 basis이지만 {v1,v2,v3}\{ \bold{v}_1, \bold{v}_2, \bold{v}_3 \}는 아니다.

basis는 유일하지 않다.

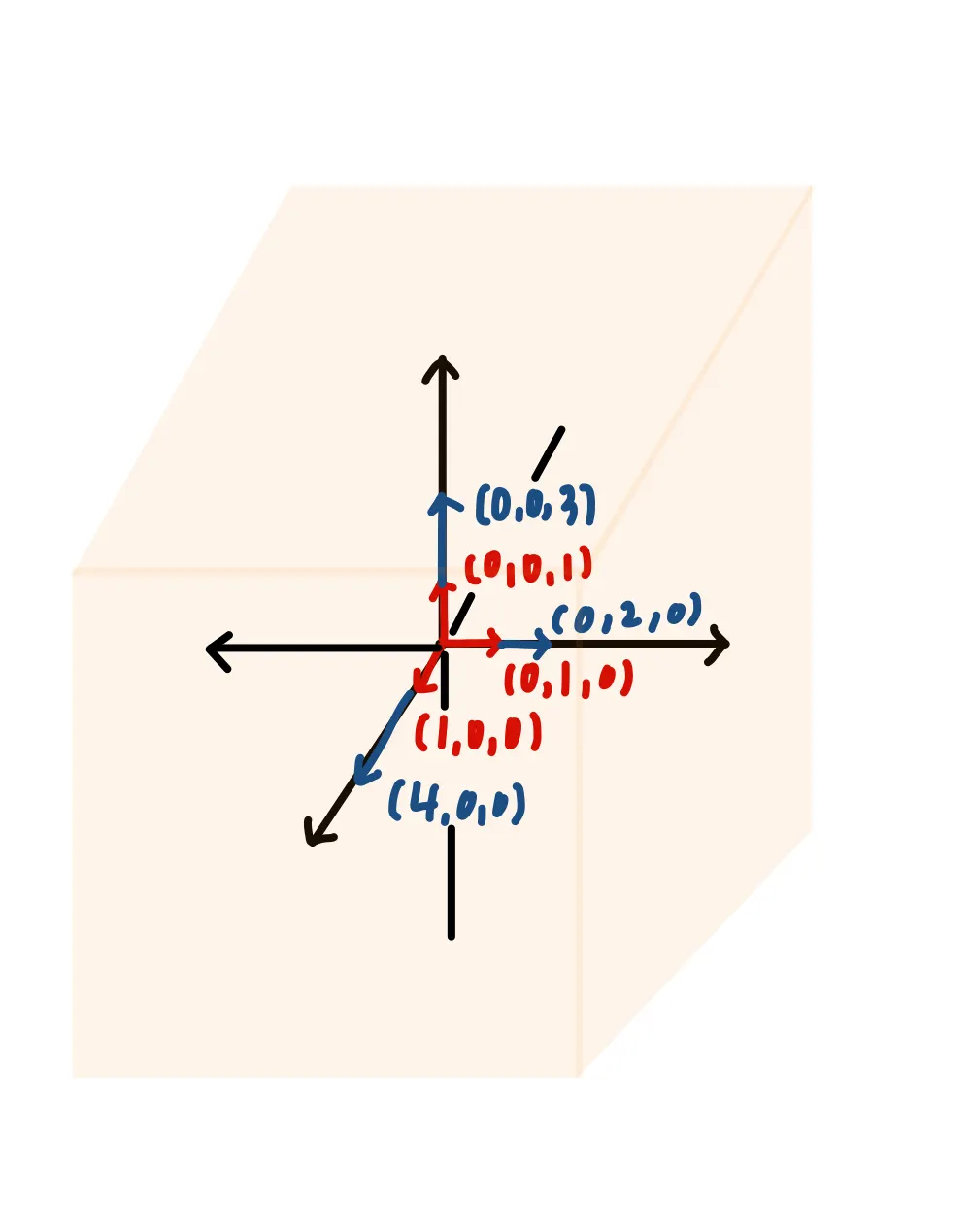
위의 예시 1)을 다시 보자.
[100],[010],[001]\begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix}, \begin{bmatrix} 0 \\ 1 \\ 0 \end{bmatrix}, \begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix} : 빨간색 벡터 [400],[020],[003]\begin{bmatrix} 4 \\ 0 \\ 0 \end{bmatrix}, \begin{bmatrix} 0 \\ 2 \\ 0 \end{bmatrix}, \begin{bmatrix} 0 \\ 0 \\ 3 \end{bmatrix} : 파란색 벡터
파란색 벡터의 집합과 빨간색 벡터의 집합 모두 이 조합으로 R3\mathbb{R}^3전체를 span할 수 있으며 선형 독립이다.

Dimension (차원)

basis는 유일하지 않지만, 주어진 subspace HH에 대해 모든 basis는 같은 수의 벡터를 가진다. 그 수가 dimension이다.
이를 the dimension of HH, dim HH 라고 표현한다.

Column space

column space of matrix AA는 AA의 columns로 span되는 subspace이다. column space of AA를 Col AA로 표현한다.
18:19
Made with