오일러경로 == 한붓그리기
쾨니히스베르크 다리 문제
그러나 이 문제는 모든 정점이 짝수개의 차수를 갖지 않아 오일러 경로가 아니다
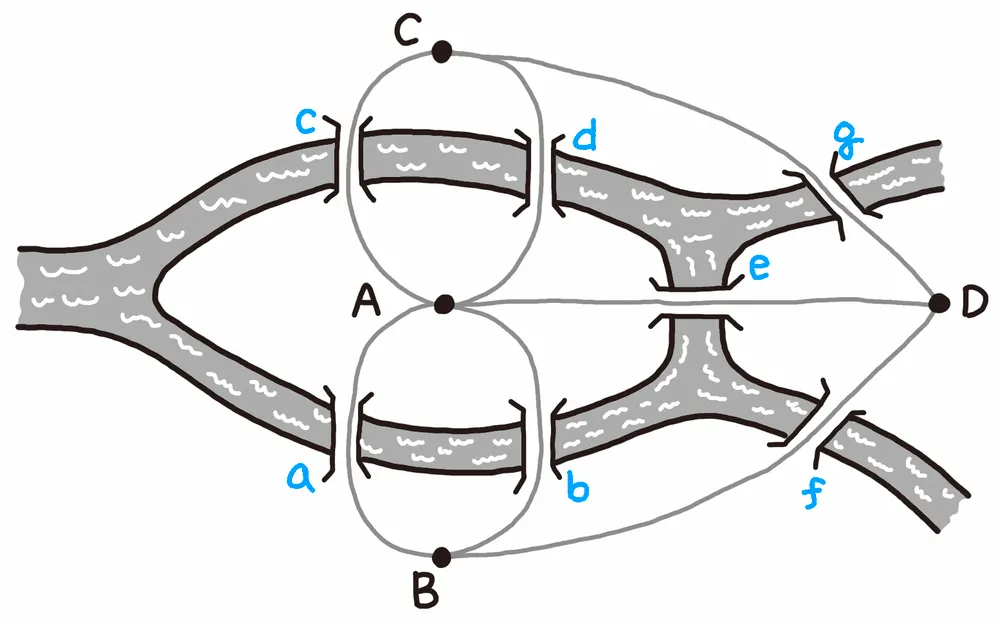
오일러는 쾨니히스베르크 다리에 a~g의 이름을 붙이고 도식화해 논문을 발표
그림의 스케치는 현대의 그래프 구조의 원형이 되었다.
A, B, C, D : 정점(vertex)
a~g : 간선(edge)
오일러의
“모든 정점이 짝수개의 차수(Degree)를 갖는다면 모든 다리를 한 번씩만 건너서 도달하는 것이 성립한다.”
는 주장을 100년도 더 뒤에 칼 히어홀저가 수학적으로 이를 증명한 것이 오일러 정리 이다.
⇒ 모든 간선을 한 번씩 방문하는 유한그래프(Finite Graph)를 오일러경로(Eulerian Trail, Eulerian Path)라고 한다
해밀턴경로
“각 정점을 한 번씩 방문하는 무향 혹은 유향 그래프 경로”
해밀턴경로 | 정점을 기준 |
오일러경로 | 간선을 기준 |
해밀턴 경로를 찾는 문제는 최적 알고리즘이 없는 대표적인 NP-Complete problem이다(NP문제 중 난해인 문제)
원래의 출발점으로 돌아오는 경로 : 특별히 해밀턴 순환 이라고 불린다
이 중 최단 거리를 찾는 문제는 알고리즘 분야에서 외판원 문제(Salesman Problem)로 유명하다
외판원 문제(Traveling Salesman Problem, TSP) : 각 도시를 방문하고 돌아오는 가장 짧은 경로를 찾는 문제 (최단 거리인 해밀턴 순환을 찾는 문제) , NP-Hard 문제로 Theoretical Computer Science 분야의 매우 중요한 문제 중 하나
이 문제에서 도시가 20개라면, 문제의 정답을 찾기 위해 다녀야하는 총 경로 수
왜 해밀턴 경로 문제와 외판원 문제의 NP문제가 다를까?
해밀턴경로 | 한 번만 방문하는 경로 |
해밀턴순환 | 한 번만 방문해 출발지로 돌아오는 경로 |
외판원 문제 | 한 번만 방문하여 출발지로 돌아오는 경로 중 가장 짧은 경로 |
외판원 문제 재정의
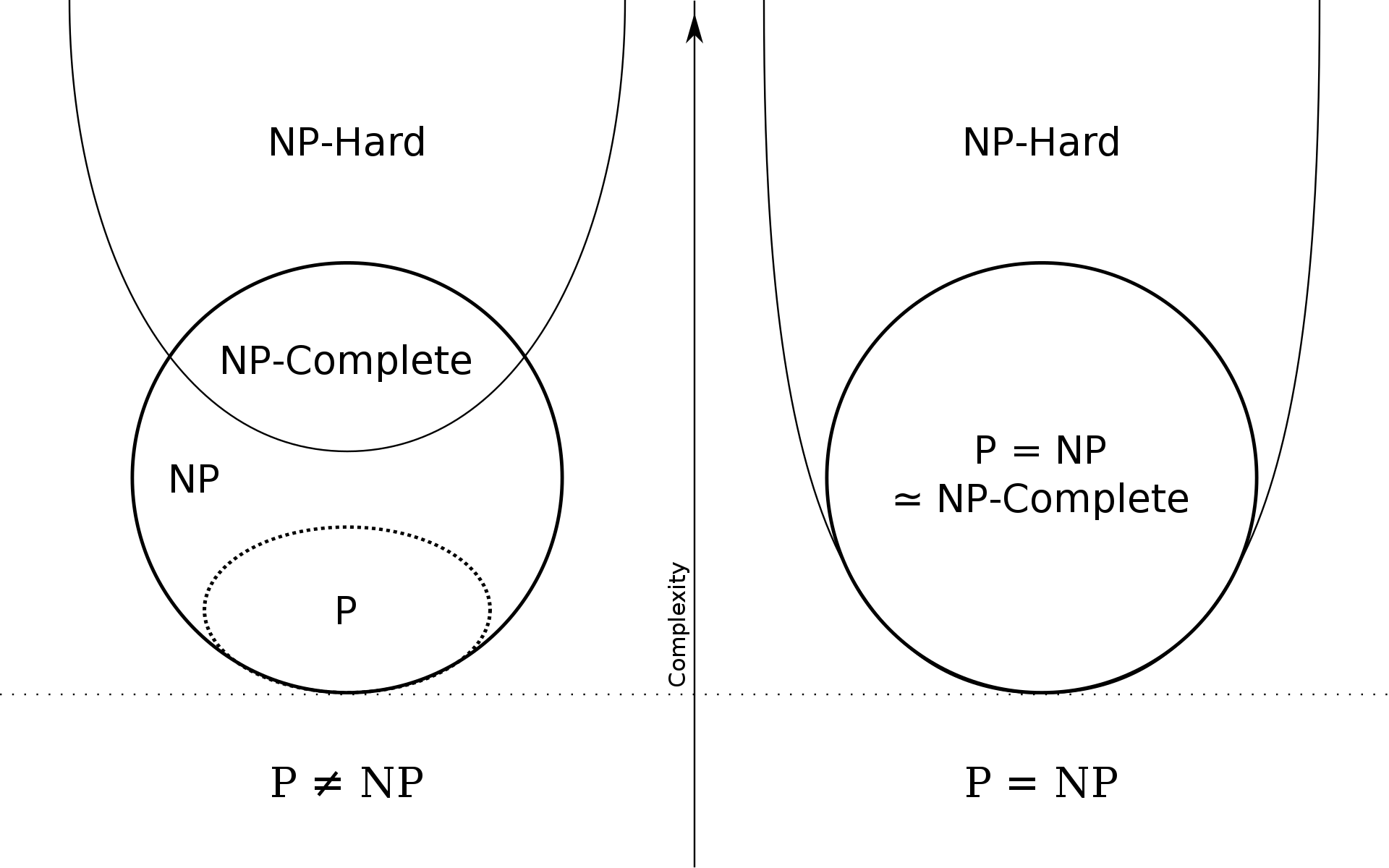
NP-Complete Problem의 조건
1. NP 문제임
2. NP-Hard 문제임
1.
해밀턴 경로가 존재하는가?
= dicision problem = 다항시간에 정답을 검증 가능 = NP문제이자 NP-Hard문제
= NP complete problem
2.
각 도시를 방문하고 돌아오는 가장 짧은 경로를 찾아라( 최단 거리의 해밀턴 순환을 찾아라 )
≠ dicision problem ⇒ NP문제가 아닐 수도 있다.
증명할 수 있는 NP-Hard 문제이지만, NP문제가 아닐 수 있으므로 NP-complete problem이 아닌 NP-hard problem
두 문제 사이의 차이를 판별해야 한다.
외판원 문제는 후에 다룰 다이나믹 프로그래밍 기법을 활용하면 좀 더 최적화 할 수 있다.
