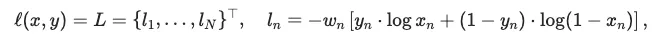Search

GAN의 MinMax Loss

minmax Loss
minGmaxD  V(D,G)=Ex∼Pdata(x)[  log⁡(D(x))  ]+Ez∼Pz(z)[  log⁡(1−D(G(z)))  ]\underset{G}{min}\underset{D}{max}\;V(D, G) =\mathbb{E}_{x\sim P_{data}(x)} [\;\log(D(x))\;] +\mathbb{E}_{z\sim P_{z}(z)}[\;\log(1-D(G(z)))\;]
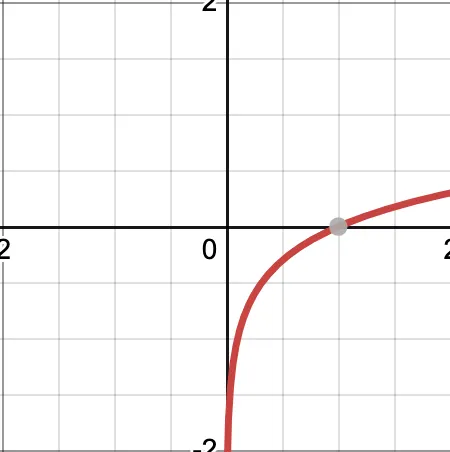
log(x)그래프
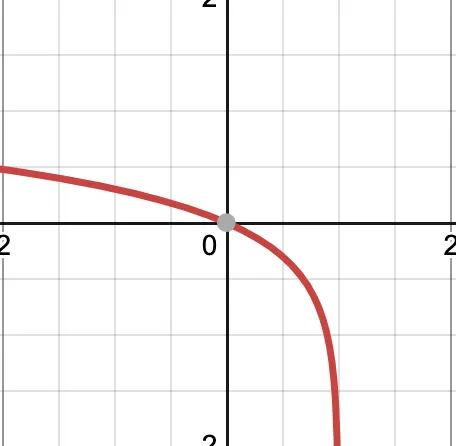
log(1-x)그래프
그래프와 코드를 함께 보면 편할 것 같다
BCELoss로 이 식을 구현한다.
criterion = nn.BCELoss() #### D update part 1 output = netD(real).view(-1) D_real_loss = criterion(output, label) # label = 1(real) #### D update part 2 fake = netG(z) output = netD(fake).view(-1) D_fake_loss = criterion(output, label) # label = 0(fake) #### G update output = netD(fake).view(-1) G_loss = criterion(output, label) # label = 1(real)
Python
복사
pytorch nn.BCELoss()
간단히 말해서, D는 real을 real로, fake는 fake로 판단하는 방향으로 학습해야하고
G는 생성한 fake를 D가 real로 판단하는 방향으로 학습해야한다
D update part 1 - real image가 input
Ex∼Pdata(x)[  log⁡(D(x))  ]E_{x\sim P_{data}(x)} [\;\log(D(x))\;] 이 식을 maximize해야하고, 이는 −log⁡(D(x))-\log(D(x))를 최소화하는 것과 같다.
real 데이터를 input으로 넣기 때문에 BCE Loss 식에 target 값을 1(real)로 넣으면 −log⁡(x)-\log(x) 식이 되므로,
output 또한 1이 나와야 −log(x)- log(x)가 최소화된다
따라서 criterion(output, label=1)의 형태로 loss 를 지정한다
D update part 2 - fake image가 input
Ex∼Pdata(x)[  log⁡(1−D(G(z)))  ]E_{x\sim P_{data}(x)}[\;\log(1-D(G(z)))\;] 이 식을 maximize해야하고, 이는 −log⁡(1−D(G(z)))-\log(1-D(G(z)))를 최소화하는 것과 같다.
fake 를 input으로 넣기 때문에 BCE Loss 식에 target 값을 0로 넣으면 −log⁡(1−x)-\log(1-x) 식이 되므로,
output 또한 0이 나와야 −log⁡(1−x)-\log(1-x) 가 최소화된다
따라서 criterion(output, label=0)의 형태로 loss 를 지정한다
G update
Ex∼Pdata(x)[  log⁡(1−D(G(z)))  ]E_{x\sim P_{data}(x)}[\;\log(1-D(G(z)))\;] 식을 minimize해야한다
D(G(z))D(G(z))값은 [01][0 \quad 1]의 범위를 가지므로 D(G(z))D(G(z))가 1에 가까워야 저 loss식이 minimize된다.
이는 −log(D(G(z)))-log(D(G(z))) 를 최소화하는 것과 같게 된다.
따라서 target값에 1을 넣고
criterion(output, label=1)의 형태로 loss를 지정한다
Made with