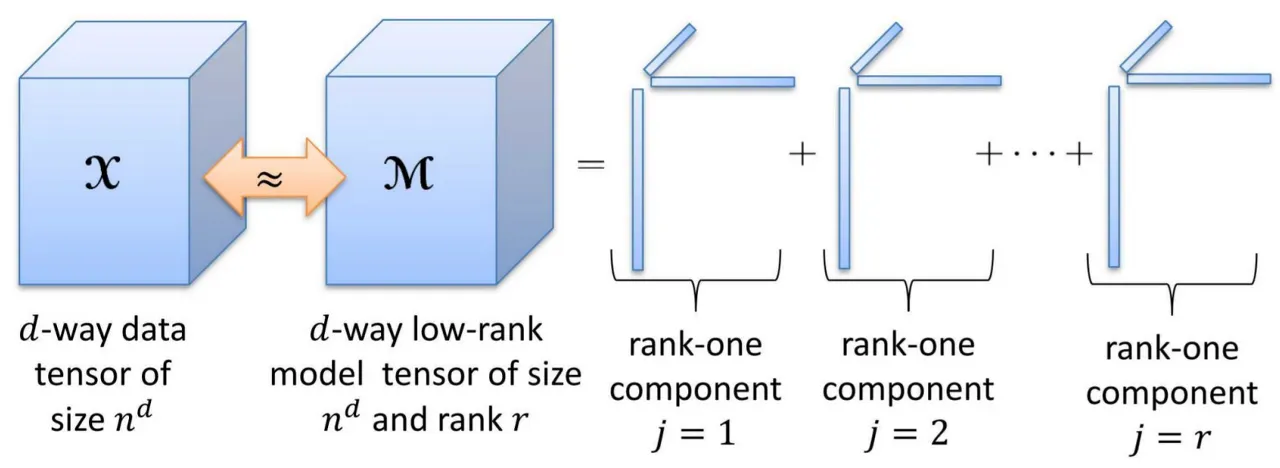
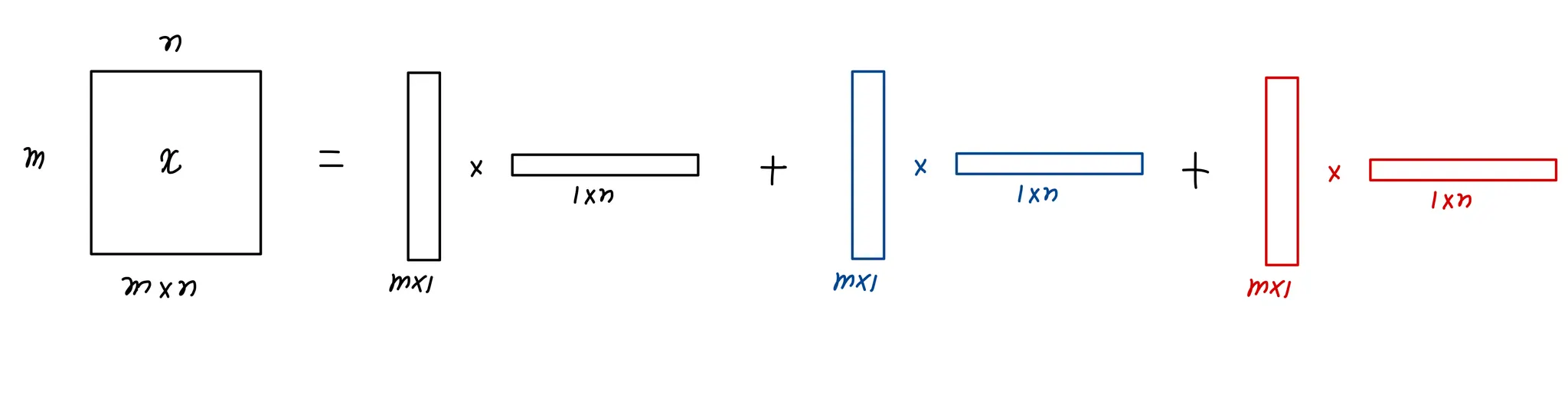tensor : N차원의 행렬
입력데이터 텐서와 가장 유사한 어떻게 찾을까
→ 여러 vector의 곱의 합 으로 구할 수 있을 것이다
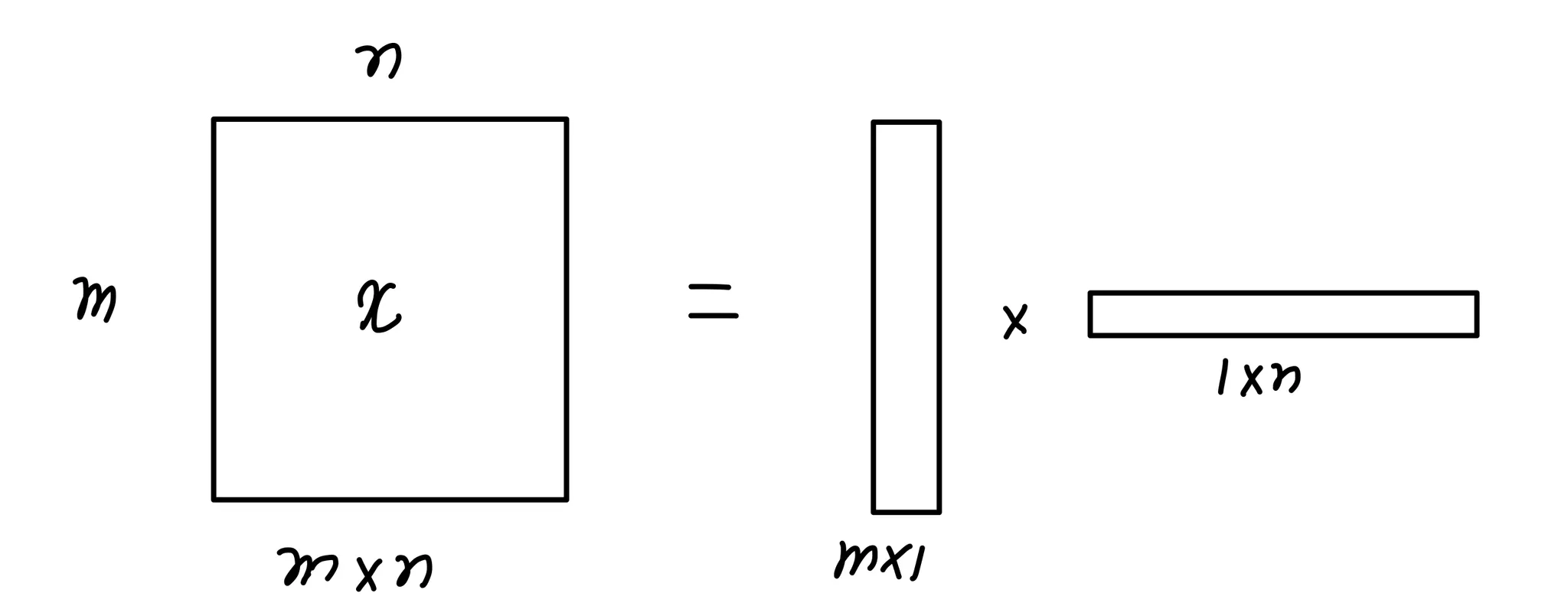
(mxn)크기의 x 행렬은 (mx1)크기의 행렬과 (1xn)크기의 행렬의 곱으로 나타낼 수 있다
→ m vector와 n vector의 곱으로 나타냄 : Matrix Factorization
그러나 정보량 차이가 있어 한번의 곱으로는 x행렬과 완전히 동일해지기가 어렵기 때문에 vector의 곱셈을 더하는 방식으로 해결할 수 있다.
첫번째 vector곱으로 x와 최대한 유사하도록 학습한 뒤 해결되지 않은 오차를 나머지 vector 곱을 추가해 해결한다.
⇒ 더 많은 vector를 사용할수록 x와 유사하게 만들 수 있다.
Tensor Decomposition 종류 두가지
1.
CP-Decomposition ( Candecomp / Parafac )
단순히 독립적이 factor들의 합을로 구성해 factor 간 상관관계 무시
2.
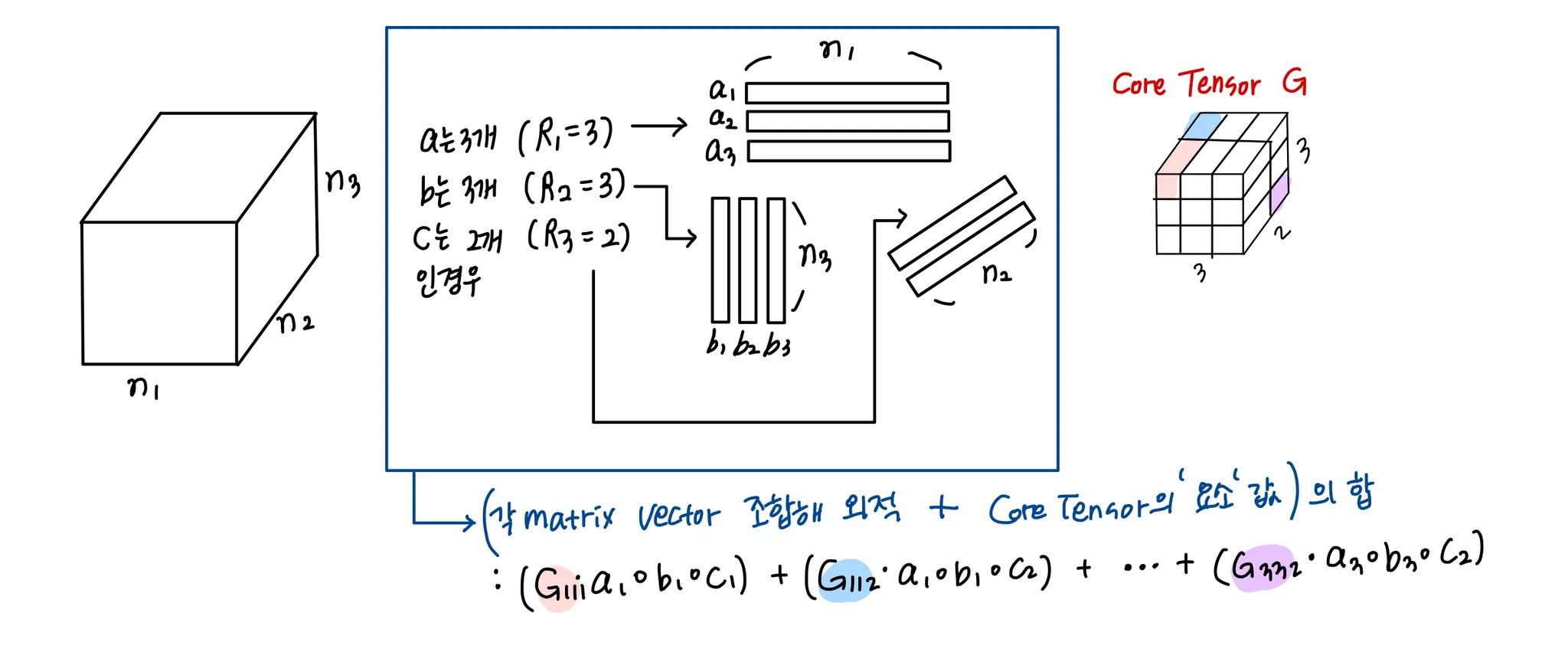
Tucker Decomposition
core Tensor를 통해 factor 간 상관관계를 고려
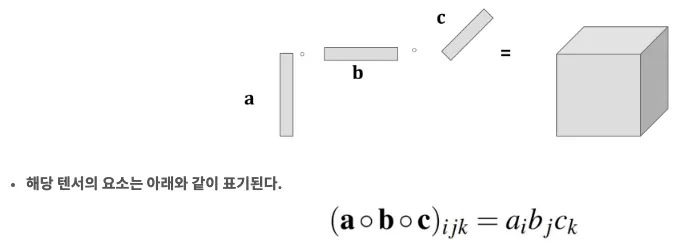
CP composition의 objective function :
a, b, c 의 외적은 하나의 rank가 되고 rank는 총 R개가 존재하게 되어 이 식을 최소화하는 것이 CP Decomposition의 목적이 된다. ( Rank의 합이 x와 유사할수록 이 식이 최소가 됨 )
Tucker Decomposition의 objective function :
CP Decomposition과 달리 a vector / b vector / c vector의 개수가 모두 다를 수 있다.
CP composition | 연산이 빠르고 정보량이 적음 |
Turker Decomposition | 연산이 느리고 정보량이 많음 |