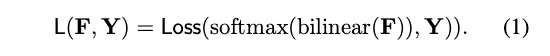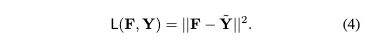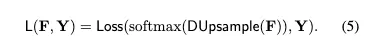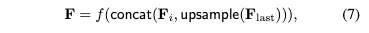💗

Decoders Matter for Semantic Segmentation: Data-Dependent Decoding Enables Flexible Feature Aggregation (CVPR2019)

openaccess.thecvf.com

https://openaccess.thecvf.com/content_CVPR_2019/papers/Tian_Decoders_Matter_for_Semantic_Segmentation_Data-Dependent_Decoding_Enables_Flexible_Feature_CVPR_2019_paper.pdf

Abstract

최근 semantic segmentation 모델들 → encoder-decoder 구조

decoder의 마지막 레이어는 보통 bilinear unsampling이었다. 이에 대한 문제를 제기

bilinear는 너무 simple하고 data에 독립적이다. 이것이 최적의 결과를 가져오지 못하게 할 수 있다고 주장하며 새로운 upsampling 방법인 DUpsampling을 제안한다. DUpsampling은 date-dependent하다. 즉, 데이터에 맞추어 학습이 가능하다.

DUpsampling은 semantic segmentation 모델들의 반복성을 통해 bilinear를 쉽게 대체 가능하다.

또한 복잡도 증가 없이 작은 해상도의 feature maps로부터 predict label map을 생성하고, 더 나은 정확도를 달성한다.

이를 달성할 수 있었던 원인은

DUpsampling은 reconstruction capability를 매우 향상시킨다. 

CNN encoder의 arbitrary combination으로 인한 DUpsampling을 기반으로 설계된 decoder의 유연성의 증가

Introduction

[FCN부터의 segmentation의 발전]

•

FCN : 각 픽셀에 대한 다양한 클래스에 대한 예측 성공. 그러나 여러 stage에 걸친 strided conv와 spatial pooling으로 final image prediction이 1/32로 줄어들고 fine image structure information을 잃어 정확도가 떨어지게 된다. 특히 객체의 경계가 심하다. 

•

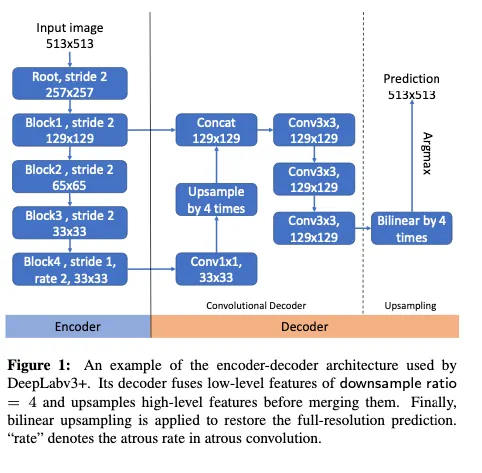
DeepLab : atrous convolutions를 통해 large receptive를 가질 수 있도록 하고 피쳐맵의 큰 해상도를 유지했다. encoder-decoder 구조를 활용했다. 

encoder-decoder구조는 backbone CNN을 encoder로 보고, raw input image를 작은 해상도의 feature map으로 encoding할 수 있는 능력을 가졌다라고 가정한다.

그 후, decoder가 작은 해상도의 피쳐맵으로부터 pixel-wise prediction을 복원한다. 이전연구의 decoder들은 몇개 없는 conv 레이어들과 bilinear upsampling을 가진다.

lightweight decoder같은 경우에는 큰 해상도의 featuremap과 bilinear upsampling을 가진다는 특징이 있다.

decoder는 보통 convolution 연산과 pooling으로 인해 잃은 fine-grained information을 캡쳐하기 위해 low-level features를 fuse한다.

[기존 segmentation의 제약]

decoder에서 input size의 1/4 , 1/8 등의 비율로 작은 feature maps로부터 input 크기의 prediction을 생성해야한다는 요구는 두가지 issue를 발생시킨다

encoder의 전체적 strides는 여러개의 atrous conv를 사용함으로써 매우 aggresively하게 줄어들어야 한다

ex) DeepLabv3 + 는 encoder에서 전체 strides를 4번에 걸쳐 32에서 8로 감소시켰다. 그래서 inference가 매우 느리다.

decoder는 보통 high level features와 very low levels features를 fuse해야한다. 

왜? bilinear의 무능력함 때문에 final prediction의 정교함은 사실 fused low-level features의 resolution에 지배되기 때문이다.

ex) Fig 1에 그려진 DeepLabv3+의 간략한 구조에서 concat이후 conv를 거치는 부분.

이러한 제약들 → 설계에 한계를 두게됨 → features를 aggregate함에 있어서 suboptimal combinations를 선택하게됨.

이논문의 실험에서는 이러한 제약없이 feature aggregation이 디자인될 수 있다면 더 나은 feature aggregation 전략을 찾을 수 있다는 것을 보여준다.

지금까지 언급한 bilinear의 단점으로, data-dependent upsampling method인 DUpsampling을 제안한다. → coarse CNNs outputs로부터 더 정확한 pixel-wise prediction 생성

새로운 DUpsampling으로 computation time과 memory footprint를 드라마틱하게 감소시켰다.

[DUsampling의 효율성]

DUpsampling은 효율적이기도 하다. decoder가 작은 resolution의 피쳐들을 합치기 전에 downsample을 할 수 있도록 해주었기 때문이다. 이게 왜 좋냐면, 작은 피쳐맵으로 연산을 수행하면 연산량이 줄고, fused features의 해상도와 마지막 prediction을 분리시킬 수 있기 때문이다. (decoupling)

이러한 decoupling은 decoder가 다양한 크기의 피쳐들을 합치고 더 나은 feature aggregation을 만들 수 있게 합니다. → segmentation 성능 향상!

[DUsampling의 이식 편리성]

DUsampling은 일반 1x1 conv가 결합된 것으로 볼 수 있기 때문에 ad-hoc(즉석) coding이 필요없다.

[contributions]

•

convolutional decoder의 coarse output으로부터 pixel-wise segmentation prediction을 복구할 수 있는 효과적인 data-dependent upsampling(DUpsampling)제안. 이전 방식에 bilinear를 쉽게 대체할 수 있다.

•

DUpsampling을 사용함으로써 전체적인 strids를 과도하게 줄이는 것을 막을 수 있다. 그래서 연산 시간과 memory footprint를 3배 이상 줄일 수 있다

•

DUpsampling은 decoder가 fused features를 merging 전에 더 낮은 해상도로 downsample할 수 있도록 한다. downsampling은 연산량을 줄일 뿐 아니라 feature aggregation의 design space도 증가시켜 더 나은 feature aggregation을 가능하게 한다.

•

위의 contributions로 새로운 decoder scheme을 제안한다. 훨씬 낮은 연산 복잡도를 가지고 SOTA decoders와 비교를 수행한다. Fig2와 같은 framework를 구성해 새로운 SOTA 성능을 달성했다. 

→ PASCAL VOC에서 88.1

\%^2

의 mIOU와 30% 낮은 연산량 달성

Related Work

Atrous convolution

Encoder-decoder architectures

Our Approach

3.1. Beyond Bilinear: Data-dependent Upsampling

일단 이 section에선 simplest decoder를 고려한다.

•

F∈RH~×W~×C~\bold{F} \in \mathbb{R}^{\widetilde{H} \times \widetilde{W} \times \widetilde{C}}F∈RH×W×C : encoder CNN의 final output

•

Y∈{0,1}H×W×C\bold{Y} \in \{0, 1\}^{{H} \times {W}\times C}Y∈{0,1}H×W×C : one-hot encoding된 ground truth label map

•

H~H=W~W=116  or  132\frac{\widetilde{H}}{H} = \frac{\widetilde{W}}{W} = \frac{1}{16} \; or  \; \frac{1}{32}HH​=WW​=161​or321​ 

training loss 연산 이전에

\bold{F}

는

\bold{Y}

의 spatial size로 upsample되어야한다.

traing loss 연산

여기서 bilinear이 최적의 upsample 방식이 아니라는 것이 이 논문의 주장이다. 너무 단순하고, reconstruction quality의 상한선이 낮다는 것이다.

bilinear로 인한 loss를 보완하기 위해서는 bilinear전의 feature maps가 최대한 high resolution이어야 한다. 그를 위한 solution으로 나온 것이 높은 연산 복잡도를 감안하고 사용하는 atrous convolutions의 적용이었다.

label

\bold{Y}

는 i.i.d(independent and identical distribution)가 아니고, 따라서 거의 loss없이 잘 압축될 수 있는 structure information을 담고있다.

그래서 이전 방식들과 달리

\bold{Y}

를

\bold{F}

크기로 압축했다.

기존 방식들	$\bold{F}$ 를 $\bold{Y}$ 의 해상도로 upsample
이 논문 방식	$\bold{Y}$ 를 $\bold{F}$ 해상도로 compress(downsample)

\bold{Y} → \widetilde{\bold{Y}}

로 compress 하는 방식

•

rrr = H\bold{H}H의 H~\widetilde{\bold{H}}H 에 대한 비율. 보통 16 혹은 32

Y\bold{Y}Y를 Hr×Wr\frac{H}{r} \times \frac{W}{r}rH​×rW​개의 grid로 분할 → r×rr \times rr×r 크기의 sub-windows로 분할. 
(만약 rrr 로 나누어떨어지지 않으면 패딩을 수행한다.

각 subwindow를 S∈{0,1}r×r×C\bold{S} \in \{ 0, 1 \}^{r \times r \times C}S∈{0,1}r×r×C 라고 정의하고,S \bold{S}S를 vector v∈{0,1}Nv \in \{ 0, 1 \}^Nv∈{0,1}N 으로 reshape한다. (N=r×r×CN=r \times r \times CN=r×r×C)

마지막으로 vector vvv 를 더 낮은 차원의 vector x∈RC~x \in \mathbb{R}^{\widetilde{C}}x∈RC로 compress하고 xxx의 값들을 vertically & horizontally stack해 Y\bold{Y}Y의 형태로 만든다.

compression 하는건 다양한 방식이 있겠지만 simple하게 linear projecting을 사용했다고 한다.

i.e.,

v

를 matrix

\bold{P} \in \mathbb{R}^{C \times N}

으로 곱해주는 것이 잘 작동했다

→ 수식 :

\bold{x} = \bold{P} v\;; \;\widetilde{v}= \bold{W}x

\bold{P}

는

v

를

x

로 compress하기 위해 사용되고,

\bold{W}\in\mathbb{R}^{N\times\widetilde{C}}

는 inverse projection matrix / reconstruction matrix로,

x

를

v

로 되돌리는데 사용된다.

\widetilde{v}

는 reconstructed

v

이다.

여기서 offset term은 생략했다고 한다. 실제 구현시에는 compression이전에 v가 training set의 평균을 빼줌으로써 centered된다.

\bold{P}

와

\bold{W}

는 training set에 대해서

v

와

\widetilde{v}

의 reconstruction error를 minimize 해야한다.

이 objective는 SGD를 통해 반복적으로 최적화된다.

orthogonality constraint를 통해 간단히 PCA를 적용해 objective에 대한 closed-form solution을 얻을 수 있다.

\widetilde{\bold{Y}}

를 target으로 사용해 compressed label

\widetilde{\bold{Y}}

가 real-valued라는 것을 관찰함으로써 regression loss가 있는 network를 pretrain할 수 있다.

어떠한 regression loss던,

{l}_2

는 일반적인 예시이다. 여기서도 (4)의 식과 같이 적용될 수 있다.

대신 더 직접적인 접근은

\bold{Y}

space 안에서 loss를 계산하는 것이다.

그러므로

\bold{Y}

를

\widetilde{\bold{Y}}

로 압축하는 대신 learned reconstruction matrix

\bold{W}

로

\bold{F}

를 upsample해서 decompressed

\bold{F}

와

\bold{Y}

사이의 pixel classiication loss를 계산한다.

linear construction→

DUpsample(\bold{F})

는 tensor

\bold{F}

안에 각 feature

\bold{f}\in \mathbb{R}^{\widetilde{C}}

에 대해 linear upsampling

\bold{W}\bold{f}

를 수행한다.

Eq. (1)과 비교하면 bilinear를 ground truth labels로부터 학습된 data-dependent upsampling로 대체했다.

이러한 upsampling 과정은 기본적으로 1x1 convolution을 spatial dimension에서 적용하는 것과 같다.(convolutional kernels는 W에 저장)

이러한 decompression은 Fig3에 표현되어 있다.

이렇게 제시된 linear upsampling외에도 upsampling위해 non-linear auto-encoder도 실험해봤다고 한다.

auto-encoder의 training또한 reconstruction loss를 최소화하기 위해 이루어졌고, linear case보다 더 일반적이었다. 경험적으로, final semantic prediction accuracy가 훨씬 간단한 linear reconstruction을 사용하는 것과 거의 비슷했다. 그래서 linear recontruction을 사용하는데에 계속해서 focus하겠다고 함.

class DUpsampling(nn.Module):
    """DUsampling module"""

    def __init__(self, in_channels, out_channels, scale_factor=2, **kwargs):
        super(DUpsampling, self).__init__()
        self.scale_factor = scale_factor
        self.conv_w = nn.Conv2d(in_channels, out_channels * scale_factor * scale_factor, 1, bias=False)

    def forward(self, x):
        x = self.conv_w(x)
        n, c, h, w = x.size()

        # N, C, H, W --> N, W, H, C
        x = x.permute(0, 3, 2, 1).contiguous()

        # N, W, H, C --> N, W, H * scale, C // scale
        x = x.view(n, w, h * self.scale_factor, c // self.scale_factor)

        # N, W, H * scale, C // scale --> N, H * scale, W, C // scale
        x = x.permute(0, 2, 1, 3).contiguous()

        # N, H * scale, W, C // scale --> N, H * scale, W * scale, C // (scale ** 2)
        x = x.view(n, h * self.scale_factor, w * self.scale_factor, c // (self.scale_factor * self.scale_factor))

        # N, H * scale, W * scale, C // (scale ** 2) -- > N, C // (scale ** 2), H * scale, W * scale
        x = x.permute(0, 3, 1, 2)

        return x
Python
복사

Incorporating DUpsampling with Adaptive-temperature Softmax

더 나아가 DUpsampling이 semantic segmentation에서 무능한..ㅎㅎ bilinear upsampling을 대체할 수 있음을 보여준다.

다음 스텝은 DUpsampling을 end-to-end trainable system으로 encoder-decoder network에 적용하는 것이다.

DUpsampling이 1x1 conv가 될 수 있다는 것을 알아도, 바로 적용하는 것은 최적화에 있어 어려움이 있다.

아마도

\bold{W}

가 one-hot encoded

\bold{Y}

로부터 연산되기 때문에 vinilla softmax와 DUpsampling의 결합이 충분히 sharp한 activation을 생성하는데 어려움이 있다는 것을 발견했다.

결과적으로 cross-entorpy loss가 training과정에서 꼼작못하게 됐고 학습과정에서 수렴을 매우 느리게 만들었다.

이 이슈를 건드리기 위해 softmax fuction with temperature를 적용했다.

T

를 통해 softmax activation을 sharpen 혹은 soften하는 식이다.

T는 일반적 backpropagation을 통해 학습된다.

Flexible Aggregation of Convolutional features

매우 deep한 CNN들은 컴퓨터비전에서 성공하였지만 depth는 semantic segmentation에 필수적인 fine-grained information의 소실의 원인이 됐다. 여러 연구에서 low level convolutional features를 결합하는 것이 segmentation 성능을 높일 수 있다는 것이 증명되었다.

\bold{F}

를 bilinear 혹은 DUpsampling을 통해 최종 pixel-wise prediction을 생성하기 위한 궁극적인 CNN feature maps라고 하자.

\bold{F}_i

: level

i

에서 feature maps

\bold{F}_{last}

: last convolutional feature maps

단순함을 위해 low-level features의 하나의 레벨을 fusing하는 것에 집중했다. 하지만 이를 multi-level fusion으로 확장하는 것은 간단하고 아마 성능을 더욱 향상시킬 것이다.

Fig1에서 나타낸 이전 decoder들의 feature aggregation의 식

f

는 CNN을 의미하고 upsample은 보통 bilinear이었다. concat은 채널 방향 concatenation이다

이 arrangement는 2가지 문제가 있다.

fff는 upsampling이후에 적용된다. fff는 CNN이기에 연산량이 input의 spatial size에 의존한다.

더 나아가 computational overhead는 decoder가 very low level에서 features를 이용하는 것을 막는다.

fused low-level features Fi\bold{F}_iFi​와 F\bold{F}F의 resolution은 같고, 보통 마지막 prediction의 1/4크기 언저리이다.

high resolution 예측을 얻기 위해서 decoder는 오직 feature aggregation with high resolution low-level features만 선택할 수 있다.

대조적으로 이 논문의 proposed framework에서는 full-resolution prediction을 복원하기 위한 책임이 DUpsampling으로 크게 이동되었다고 한다.

그러므로 사용된 low-level features의 어떤 level이든 last feature maps

F_{last}

의 해상도로 안전하게 downsample할 수 있고 이 features를 final prediction을 위해 fuse할 수 있다.

따라서 Eq. (7)은 다음과 같이 바뀐다.

→ upsample해서 concat하는 것이 아니라 downsample해서 concat

downsample은 bilinear로 사용했다고 한다. 이는 features를 가장 낮은 해상도에서 효율적으로 연산할 뿐 아니라 low-level features

F_i

와 final segmenation prediction을 분리해 모든 level의 features를 fuse할 수 있게 한다.

실험에서

오직 앞에 언급된 DUpsampling과 결합하였을 때만 downsampling scheme이 작동한다.

그렇지 않으면 성능의 상한선이 제한된다. upsampling method가 incapable하기 때문에

이것이 이전 방식들이 low resolution high level feature maps를 upsample한 이유이다.

Experiments

datasets : PASCAL VOC, PASCAL Context, Cityscapes

Implement details

•

ablation study는 PASCAL VOC에서 시행

•

[5: deeplab v3]에서처럼 modified해서 ResNet-50과 Xception-65를 backbone network로 택함

•

모든 실험에서 learning rate policy 를 ‘poly’로 사용

•

initial learning rate 0.007

•

total iteration 30k for ablation experiments on PASCAL VOC

•

모든 ResNet base 실험에서 weight decay를 0.0001h wjrdyd.

•

batch size 48

•

batch normalization은 12개의 batch 기준으로 적용

•

모든 Xception-based experiments에서 weight decay는 0.00004

•

batch size 32그러나 batch normalization statics는 batch 16 내에서 연산

•

ImageNet pretrained weights 사용

•

새롭게 추가된 레이어들의 모든 weights는 Gaussian distribution( variance 0.01, mean 0 )으로 초기화

•

adaptive-temperature softmax의 TTT 는 1로 초기화

•

C~\widetilde{C} C는 ResNet50 대해 64, Xception-65 대해 128

•

training data를 0.5 ~ 2.0으로 randomly scaling하고 left-right flipping해서 augmentation

4.1. Ablation Study

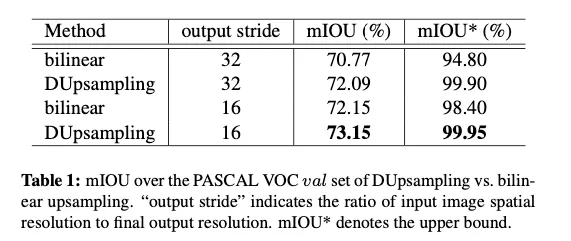
Dupsampling vs. Bilinear

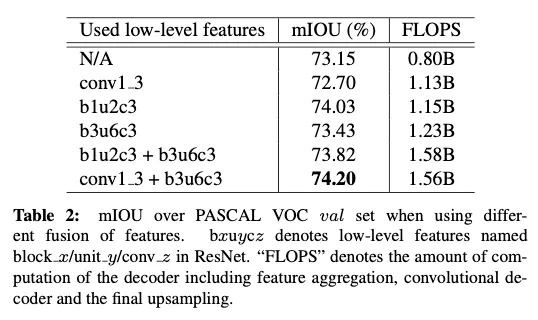
Flexible aggregation of convolutional features

comparison with the vanilla bilinear decoder

Impact of adaptive-temperature softmax