읽기 전 보면 좋은 자료 / 참고자료
Swin Transformer github : https://github.com/microsoft/Swin-Transformer
Swin Transformer paper : https://arxiv.org/pdf/2103.14030.pdf
Abstract
ViT와 같이 transformer구조를 computer vision task의 general purpose backbone 으로 쓰일 수 있게 하는 것이 목적인 논문이다.
nlp와 vision의 도메인 차이에서 발생하는 문제를 해결하기 위해 hierarchical transformer를 구성하였는데, 이는 shifted window 에서 연산하는 방식으로 가능했다. 이는 non overlapping local window를 사용하며, window간의 connection을 가능하게 한다. 또한 Swin Transformer는 다양한 스케일을 모델링하는 데에 있어 유연하고 이미지 크기에 대해 linear한 computational complexity를 가진다.
이러한 디자인은 all-MLP 아키텍쳐에 비해 다양한 이점을 가진다.
Introduction
Transformer의 NLP에서의 좋은 성능을 image로 가져오는 데에 있어 큰 어려움은 도메인의 차이에 있다.
NLP에서는 tokens가 기본 요소이지만 시각적 요소들은 스케일에 따라 형태가 다양하고 이 문제는 object detection 같은 task의 경우에 더 도드라진다.
이미 존재하는 transformer기반 이미지 모델들은 토큰들이 고정된 스케일에서 적용되고 비전에 적합하지 않다. 또한 해상도가 커짐에 따라 계산 복잡도가 quadratic하게 증가한다. 이를 극복하기 위해 Swin transformer에서는 hierarchical feature maps를 통해 계산복잡도를 linear하게 증가하도록 했다.
Proposed method
Swin transformer(Swin-T)의 전체적인 구조는 다음과 같다
•
stage 별로 위에 써져있는 식(노란색)은 VGG와 같은 기존 CNN 모델에서 나타내는 피쳐의 해상도와 같은 표현이다. hierarchical 구조라는 말과 같이 해상도는 점점 줄어들고, 채널 수는 점점 늘어난다. 마치 VGG, ResNet같은 느낌이 난다.
Patch Partition (초록색)
•
이 단계에서는 이미지를 ViT와 같이 겹치지 않도록 패치로 나누어 준다. 각 patch는 NLP에서의 token이라고 할 수 있다. 본 논문의 실험에서는 4x4패치를 사용했으며 따라서 token은 4x4x3 size이다.
Linear Embedding (파란색)
•
각 패치들을 C차원으로 임베딩하는 과정이다.
⇒ Patch Partition + Linear Embedding 과정이 stride 4, kernel size 4 (patch size와 동일)의 nn.Conv2d로 구현되어 있다.
self.proj = nn.Conv2d(in_chans, embed_dim, kernel_size=patch_size, stride=patch_size)
Python
복사
이제 stage2부터는 patch merging 과 Swin Transformer Block으로 이루어져 있다.
Patch mergning (분홍색)
2x2 이웃 패치를 concatenate 한 후 Linear Layer로 4C 채널 → C채널로 줄여준다.
""" PatchMerging code """
x = x.view(B, H, W, C)
x0 = x[:, 0::2, 0::2, :] # B H/2 W/2 C
x1 = x[:, 1::2, 0::2, :] # B H/2 W/2 C
x2 = x[:, 0::2, 1::2, :] # B H/2 W/2 C
x3 = x[:, 1::2, 1::2, :] # B H/2 W/2 C
x = torch.cat([x0, x1, x2, x3], -1) # B H/2 W/2 4*C
x = x.view(B, -1, 4 * C) # B H/2*W/2 4*C
x = self.norm(x) # nn.LayerNorm
x = self.reduction(x) # nn.Linear(4 * dim, 2 * dim, bias=False)
Python
복사
아래 그림은 이 코드를 잘 나타내는 그림이다
Swin Transformer Block
드디어 swin transformer block의 차례다.
논문에는 두개의 연속된 Swin Transformer Block의 그림이 제시되어 있다.
Swin Transformer Block
기존 Transformer Block
일반 Transformer block과 유사해보이는데 W-MSA(window based self-attention)과 SW-MSA(shifted window based self-attention)이라는 새로운 모듈을 볼 수 있다.
일단 이 새로운 window 기반 self attention들은 non-overlapping partitioning을 기반으로 한다.
각 stage의 첫번째 swin transformer block에서는 W-MSA로 다음과 같이 partitioning을 수행한다. 이렇게 나누는 window의 크기를 M이라고 정의한다 ( M=4, window size = 4x4 )
이 각 window 내에서 self attention을 수행한다. window의 개수는 H/M + W/M개가 되겠다.
window partitioning의 구현과 W-MSA의 구현을 간단하게 정리해보겠다.
""" window partitioning official code """
def window_partition(x, window_size):
"""
Args:
x: (B, H, W, C)
window_size (int): window size
Returns:
windows: (num_windows*B, window_size, window_size, C)
"""
B, H, W, C = x.shape
x = x.view(B, H // window_size, window_size, W // window_size, window_size, C)
windows = x.permute(0, 1, 3, 2, 4, 5).contiguous().view(-1, window_size, window_size, C) # (B, H//ws, W//ws, ws, ws, C) -> (B*H//ws*W//ws, ws, ws, C)
return windows
Python
복사
""" W-MSA code """
B_, N, C = x.shape # (B*patch 개수, MxM, C) 가 input으로 들어온다.
# self.qkv = nn.Linear(dim, dim * 3, bias=qkv_bias)
# N = MxM
qkv = self.qkv(x).reshape(B_, N, 3, self.num_heads, C // self.num_heads).permute(2, 0, 3, 1, 4)
# (B_, N, C) -> (B_, N, 3C) -> (B_, N, 3, self.num_heads, C // self.num_heads) -> (3, B_, self.num_heads, N, C//self.num_heads)
q, k, v = qkv[0], qkv[1], qkv[2]
q = q * self.scale
attn = (q @ k.transpose(-2, -1)) # (B_, self.num_heads, N, N) # 윈도우와 윈도우 사이의 유사도
attn = attn + relative_position_bias # relative_position_bias 에 대해서는 뒤에서 다루겠습니다
attn = self.softmax(attn)
x = (attn @ v).transpose(1, 2).reshape(B_, N, C) # (B_, self.num_heads, N,N)@(B_, self.num_heads, N, C//self.num_heads) -> (B_, self.num_heads, N, C//self.num_heads) ->reshape-> (B_, N, C)
x = self.proj(x) # self.proj = nn.Linear(dim, dim)
Python
복사
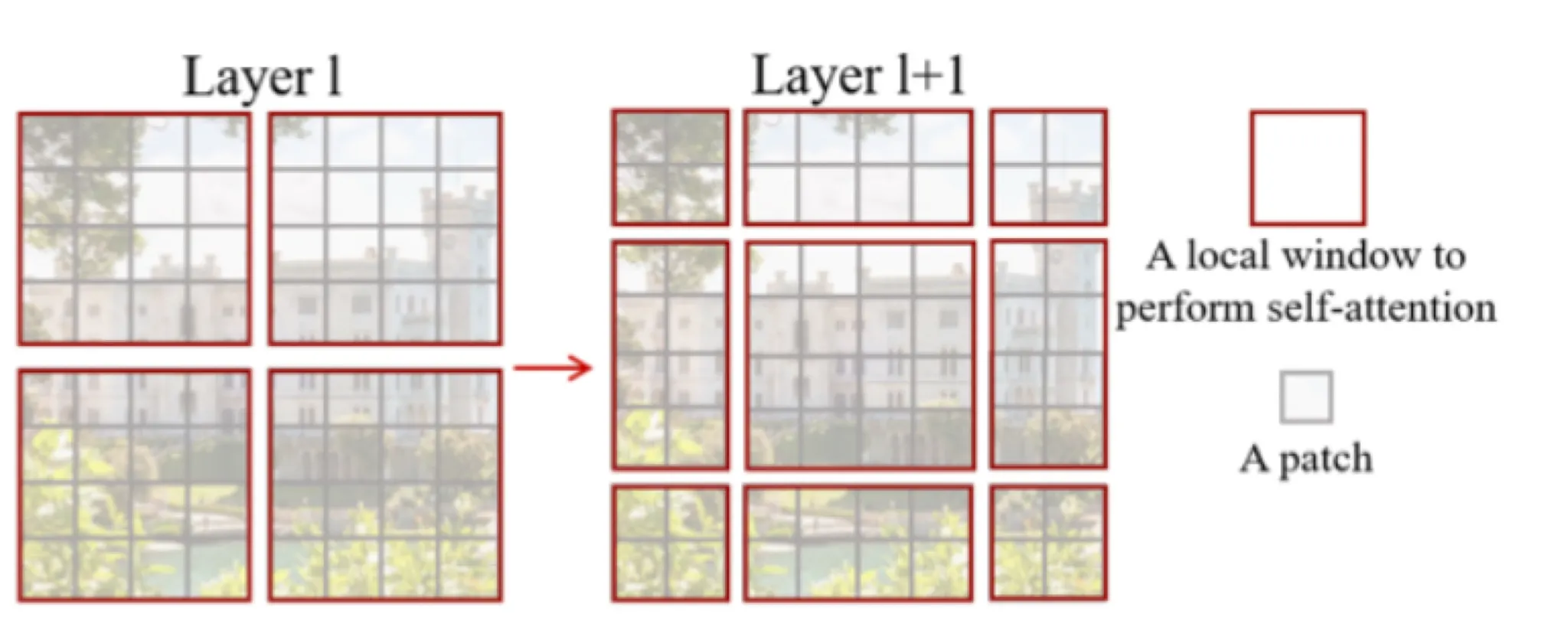
Shifted window based self attention
이제 두번째 swin transformer block부터는 SW-MSA라는 shifted window 기반 self attention 이 수행된다. 이 방식은 논문이 앞에서 주장한 고정된 스케일의 토큰 문제해결을 위해 윈도우를 일정부분 이동하여 다른 영역에서 partitioning을 수행한다. shift하는 정도는 M/2로 정했다고 한다. 그림을 보면 바로 이해할 수 있다.
이렇게 shift된 윈도우 내에서 self attention 을 수행한다.
그런데 이렇게 하면 패치수가 증가하게 된다 (2x2 → 3x3) 그래서 계산량이 많아지게 되며 패치 크기들이 달라져서 연산도 어렵다. 이를 해결하기 위해 더 효율적인 efficient batch computation approach를 제안한다.
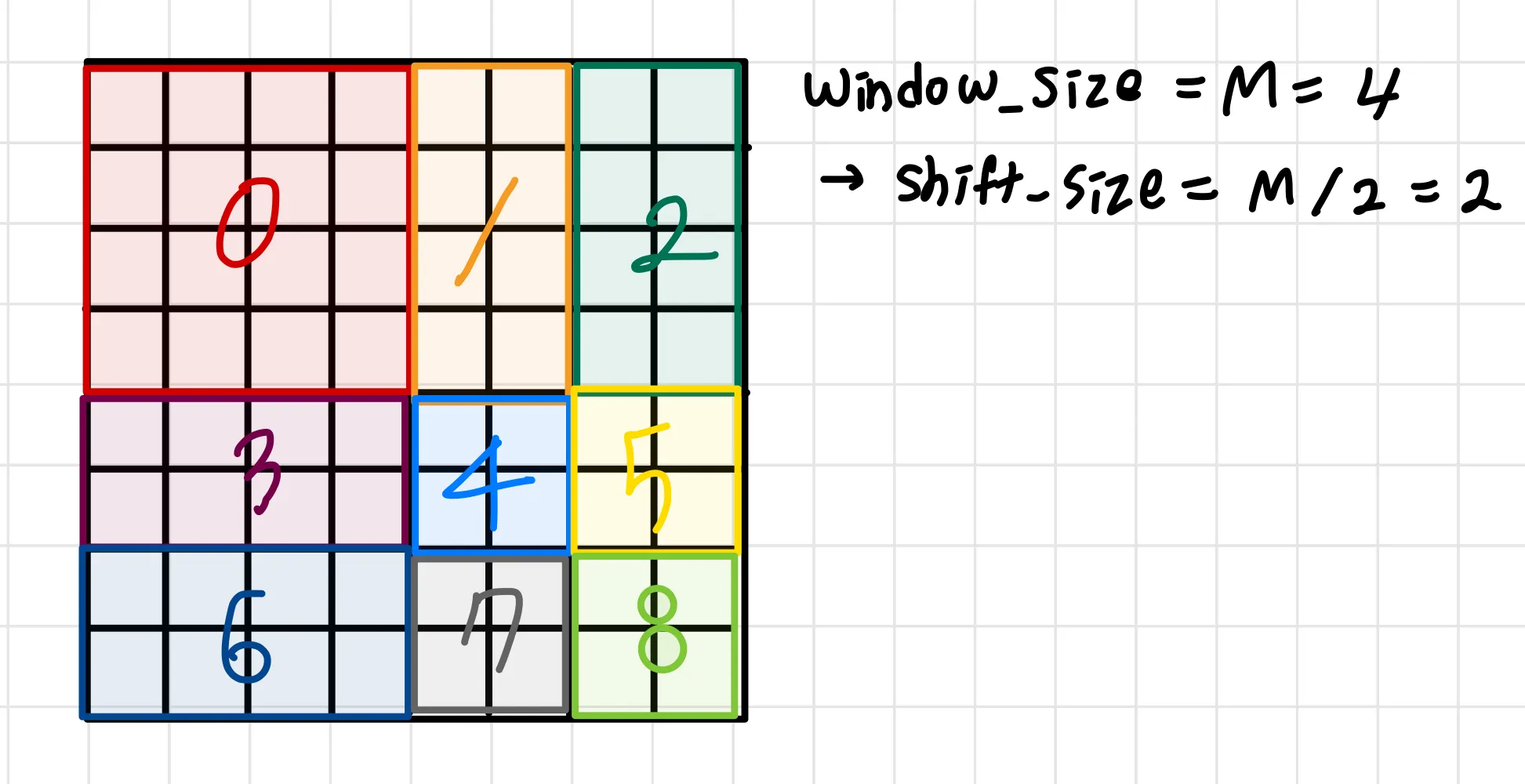
그림을 보면 알 수 있듯, shift한 크기만큼 모든 패치들을 왼쪽과 위로 이동한다. 그림에선 왼쪽으로 두칸, 위로 두칸 이동했다. 이렇게되면 한 패치 안에 원래는 이웃하지 않는 영역들이 이웃하게 된다. 이 부분은 attention 연산에 포함되면 안된다. 이를 mask를 이용해 구현하였다.
그림으로 먼저 설명하고, mask 구현 코드는 그 뒤에 다뤄보겠다.
cyclic shift한 후 W-MSA처럼 똑같이 partitioning을 수행한 후, 연산 수행 후 그림과 같은 mask를 통해 cyclic shift 하기 전 원래 partition 내의 영역끼리의 연산만을 사용하도록 해준다. 하나의 예시를 자세히 살펴보면 아래와 같다.
이 패치에서 원래의 윈도우는 빨간 영역과 파란 영역으로 나눠져야 한다. 즉, attention 연산을 할 때 빨간 영역끼리의 연산 결과, 파란 영역끼리의 연산결과만 반영이 되어야한다. 그래서 오른쪽 mask의 검정색 영역만이 attention에 반영이 되도록 해준다.
이제 구현을 살펴보겠다.
""" cyclic shift 수행 """
shifted_x = torch.roll(x, shifts=(-self.shift_size, -self.shift_size), dims=(1, 2))
""" mask 생성 """
# calculate attention mask for SW-MSA
H, W = self.input_resolution
img_mask = torch.zeros((1, H, W, 1)) # 1 H W 1
h_slices = (slice(0, -self.window_size),
slice(-self.window_size, -self.shift_size),
slice(-self.shift_size, None))
w_slices = (slice(0, -self.window_size),
slice(-self.window_size, -self.shift_size),
slice(-self.shift_size, None))
cnt = 0
for h in h_slices:
for w in w_slices:
img_mask[:, h, w, :] = cnt
cnt += 1
Python
복사
여기까지 수행했을 때 img_mask는 다음과 같다.
이어서 봐보겠다.
mask_windows = window_partition(img_mask, self.window_size)
# nW, window_size, window_size, 1 # 위의 mask에 window partitioning을 수행해준다.
# nW 는 window 개수
mask_windows = mask_windows.view(-1, self.window_size * self.window_size)
# (nW, ws*ws)
attn_mask = mask_windows.unsqueeze(1) - mask_windows.unsqueeze(2) #(nW, 1, ws*ws) - (nW, ws*ws, 1) 이렇게 하면 broadcasting 으로 결과는 (nW, ws*ws, ws*ws)가 나오게 되며 attention mask의 shape 내에서 같은 번호인 것들은 zero가 된다.
attn_mask = attn_mask.masked_fill(attn_mask != 0, float(-100.0)).masked_fill(attn_mask == 0, float(0.0))
# 그래서 0인 영역들은 0으로 채워주고 아닌 영역들은 -100으로 채워주어서 softmax를 수행했을 때 매우 작은 값을 갖도록 한다.
Python
복사
이제 이 mask가 들어가서 attention 이 수행되는 부분이다.
""" SW-MSA code """
B_, N, C = x.shape # (B*patch 개수, MxM, C) 가 input으로 들어온다.
# self.qkv = nn.Linear(dim, dim * 3, bias=qkv_bias)
qkv = self.qkv(x).reshape(B_, N, 3, self.num_heads, C // self.num_heads).permute(2, 0, 3, 1, 4)
# (B_, N, C) -> (B_, N, 3C) -> (B_, N, 3, self.num_heads, C // self.num_heads) -> (3, B_, self.num_heads, N, C//self.num_heads)
q, k, v = qkv[0], qkv[1], qkv[2]
q = q * self.scale
attn = (q @ k.transpose(-2, -1)) # (B_, self.num_heads, N, N) # 윈도우와 윈도우 사이의 유사도
attn = attn + relative_position_bias # relative_position_bias 에 대해서는 뒤에서 다루겠습니다
#### 여기까지 W-MSA 와 동일 ####
if mask is not None: # mask가 존재하면 SW-MSA로 수행
nW = mask.shape[0]
attn = attn.view(B_ // nW, nW, self.num_heads, N, N) + mask.unsqueeze(1).unsqueeze(0) # shape를 맞춰준 뒤 mask를 더해준다.
attn = attn.view(-1, self.num_heads, N, N)
attn = self.softmax(attn)
else:
# mask 없으면 그냥 W-MSA 수행 (masking 과정 필요 x)
attn = self.softmax(attn)
attn = self.attn_drop(attn)
x = (attn @ v).transpose(1, 2).reshape(B_, N, C)
x = self.proj(x)
Python
복사
이제 마지막으로 relative_position_bias를 알아보자
relative position bias
위의 식에서 B에 해당하는 부분이다.
x축과 y축 방향으로 위치에 따라 상대적인 bias를 주는 방식이다.
absolute position embedding을 사용하거나 bias term을 사용하지 않는 비교모델들에 비해 성능 개선이 많이 되었다고 한다. position embedding을 입력에 추가하는 것은 성능이 저하되었다고 하며, pretraining에서 학습된 relative position bias는 fine tuning 시에 다른 window size를 initialize하는 용도로 사용될 수 있다고 한다.(bicubic interpolation 사용)
어떤 방식인지 코드 구현을 살펴보겠다
여기서 M=3, 즉 window_size[0], window_size[1]은 3으로, num_heads=10 으로 가정하겠다.
""" relative position bias code """
# define a parameter table of relative position bias
self.relative_position_bias_table = nn.Parameter(
torch.zeros((2 * window_size[0] - 1) * (2 * window_size[1] - 1), num_heads)) # (2*Wh-1 * 2*Ww-1, nH) -> (25, 10)
trunc_normal_(self.relative_position_bias_table, std=.02)
# timm의 함수로, 표준편자 0.2이고 평균이 0인 정규분포로 값을 채운다. min은 -2, max는 2
# __init__에서 initialize 해주는 부분이다.
# get pair-wise relative position index for each token inside the window
coords_h = torch.arange(self.window_size[0]) # 0~2
coords_w = torch.arange(self.window_size[1]) # 0~2
coords = torch.stack(torch.meshgrid([coords_h, coords_w]))
# (2, Wh, Ww) -> (2, 3, 3)
Python
복사
여기서 coords는 다음과 같이 만들어진다.
위는 x축에 대한 것이고 아래는 y축에 대한 것이다.
coords_flatten = torch.flatten(coords, 1) # (2, Wh*Ww) = (2, 9)
relative_coords = coords_flatten[:, :, None] - coords_flatten[:, None, :]
# (2, Wh*Ww, Wh*Ww) = (2, 9, 9)
Python
복사
여기까지 했을 때 relative_coords는 broadcasting으로 다음과 같이 연산된다
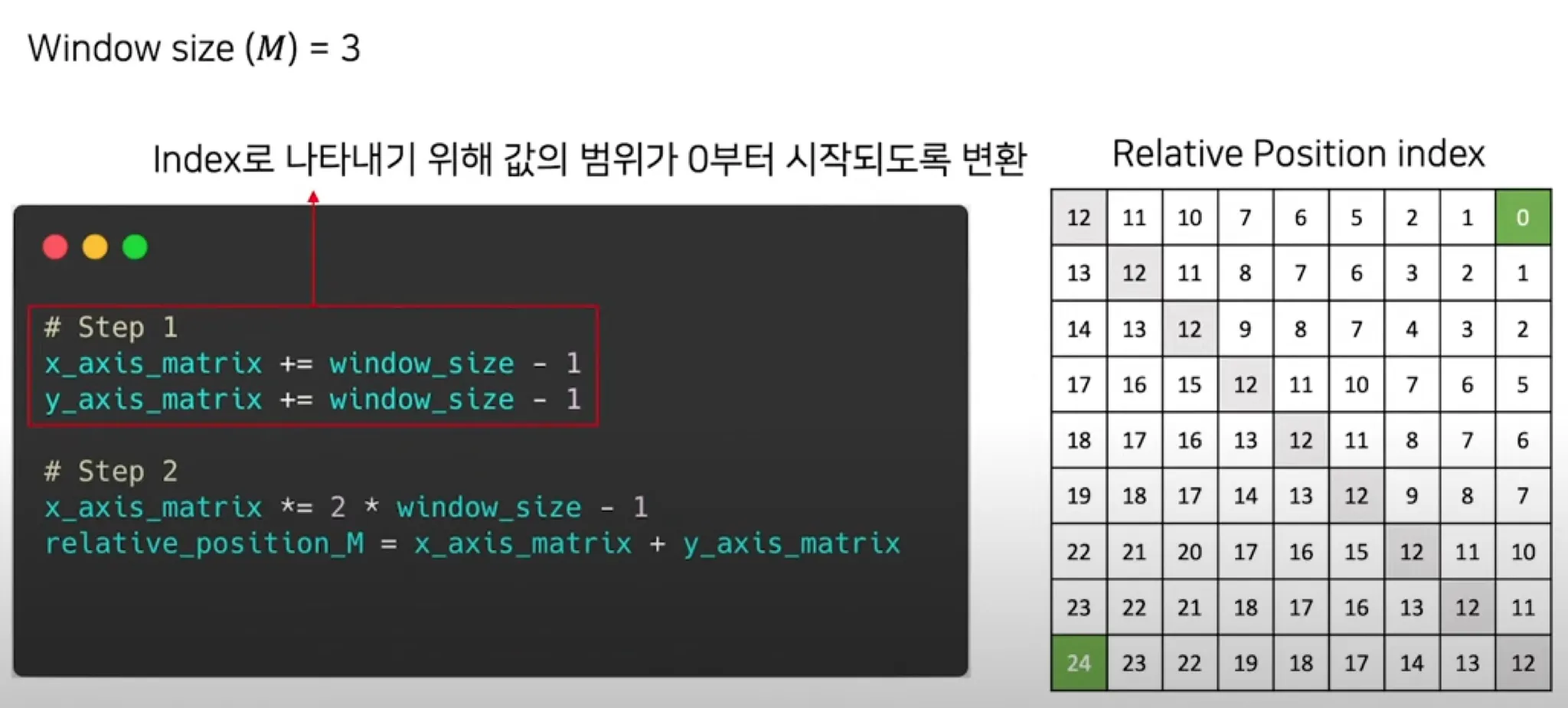
relative_coords = relative_coords.permute(1, 2, 0).contiguous() # Wh*Ww, Wh*Ww, 2
relative_coords[:, :, 0] += self.window_size[0] - 1 # shift to start from 0
relative_coords[:, :, 1] += self.window_size[1] - 1
# 값들이 -2~0의 값에서 0~2의 값으로 바뀐다
###
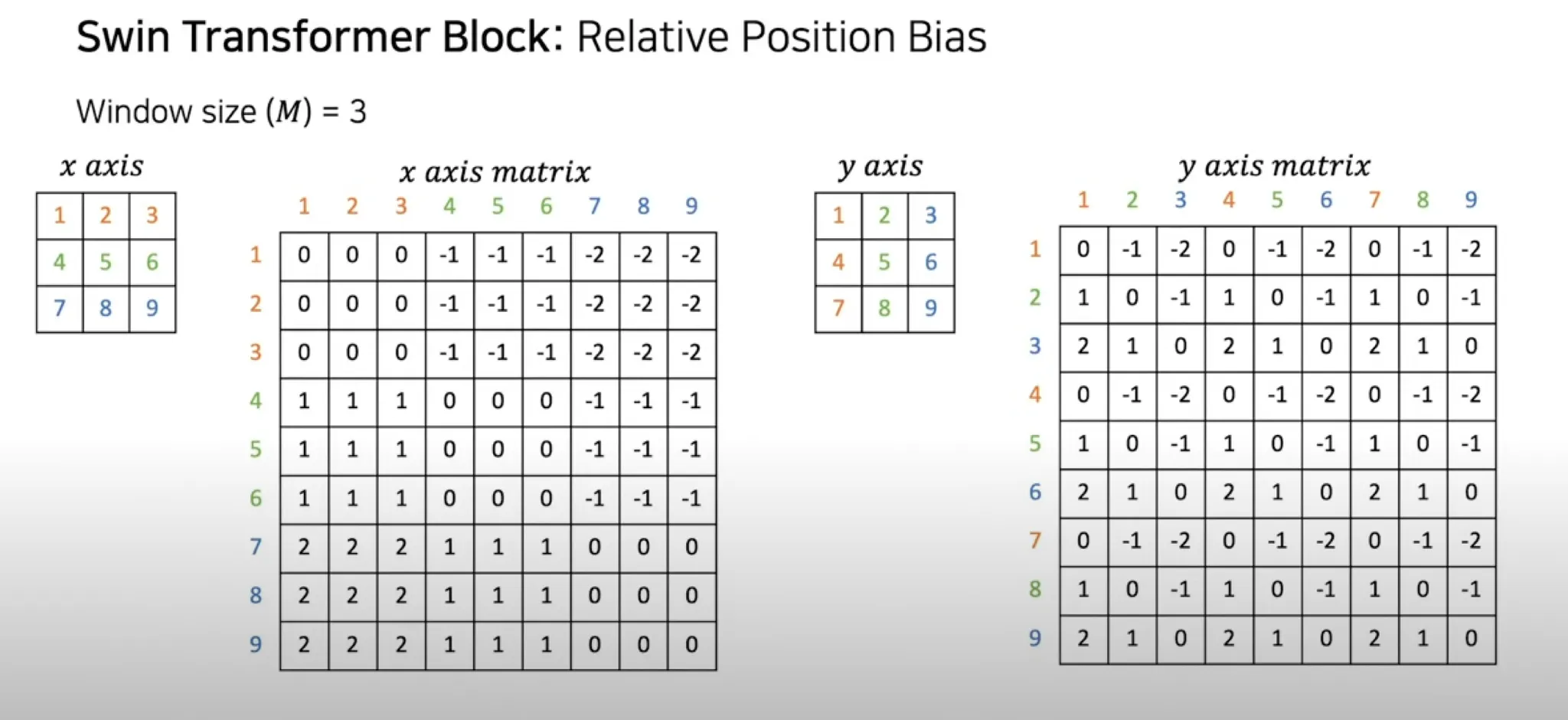
relative_coords[:, :, 0] *= 2 * self.window_size[1] - 1
relative_position_index = relative_coords.sum(-1) # Wh*Ww, Wh*Ww
"""
이 부분은 x_axis_matrix*(2*ws - 1) + y_axis_matrix로
5*x_axis_matrix + y_axis_matrix 이다.
"""
###
Python
복사
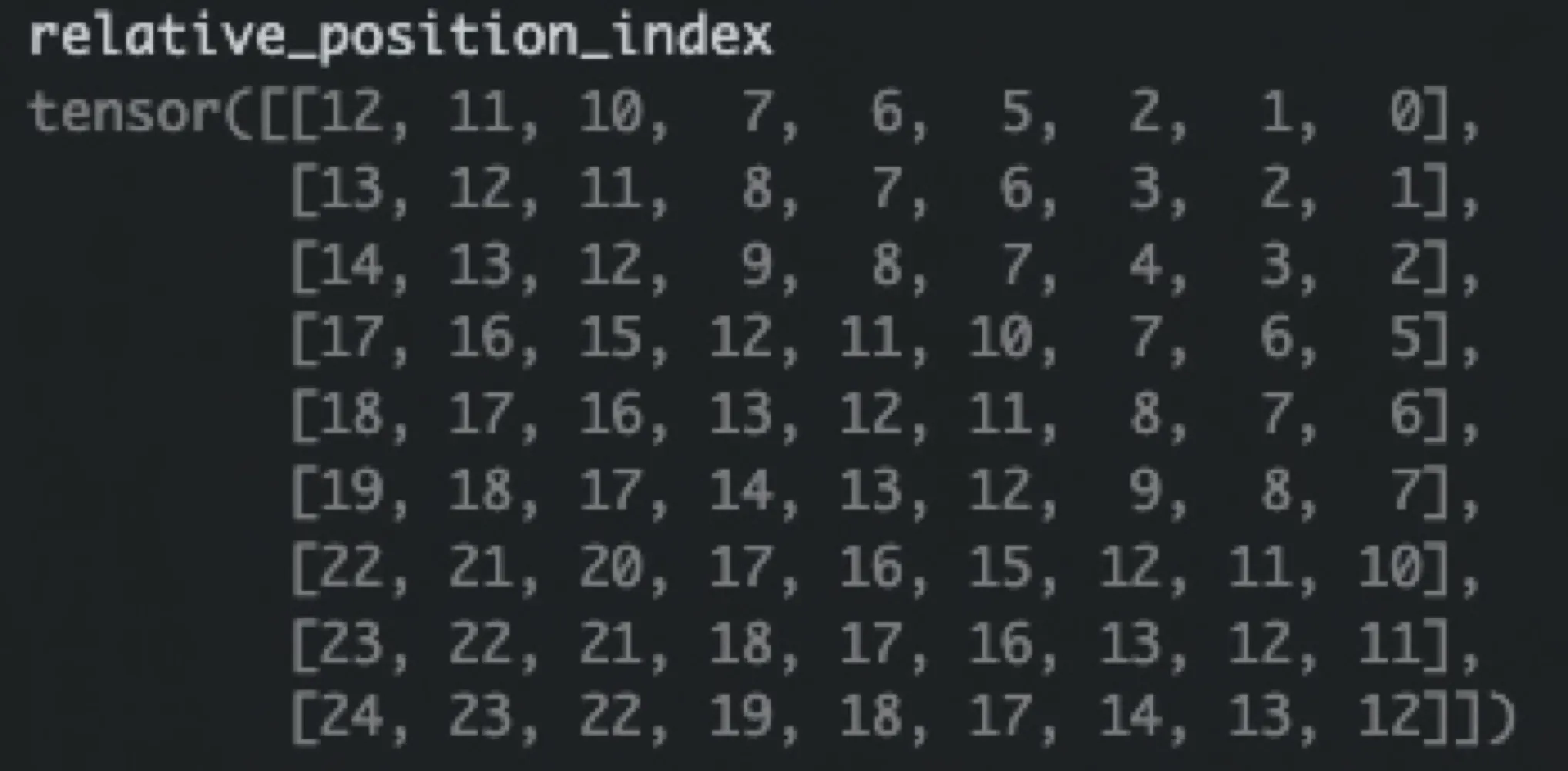
여기 까지 했을 때 relative_position_index는 다음과 같다.
relative_position_bias = self.relative_position_bias_table[self.relative_position_index.view(-1)].view(
self.window_size[0] * self.window_size[1], self.window_size[0] * self.window_size[1], -1) # Wh*Ww,Wh*Ww,nH ( (81, 10) -> (9, 9, 10) )
"""
정규분포로 채워진 relative_position_bias_table에서 앞에서 구한 index로 값을 가져오고
(ws*ws, ws*ws, num_heads) 로 reshape 해준다.
"""
relative_position_bias = relative_position_bias.permute(2, 0, 1).contiguous()
# (num_heads, ws*ws, ws*ws)
relative_position_bias = relative_position_bias.unsqueeze(0)
# (1, num_heads, ws*ws, ws*ws)
Python
복사
이를 구성한 목적은,
만약 3x3 윈도우라고 하면, (0,0)에서 (2, 2)까지 이동하려면 (2, 2)를, (2, 2)에서 (0, 0)까지 이동하려면 (-3, -3)을 이동해야 한다. 따라서 어떤 픽셀을 중심으로 하느냐에 따라 이동해야하는 값이 달라지기에 sin cos 주기로 구한 절대좌표보다 상대적 좌표를 embedding에 더해주는 것이 좋다는 것이다.
Experiments
•
EfficientNet과 비슷한 성능, ViT 계열보다 더 높은 성능을 보였다.
•
다른 task의 backbone으로 사용했을 때 성능이 거의 다 SOTA에 가까웠다.
•
shifting 의 유무에 따라 비교했을 때 SW-MSA와 W-MSA를 둘 다 사용했을 때가 가장 성능이 좋았고
•
relative position embedding 만 쓰는 것이 더 좋았다.