다익스트라 알고리즘은 다이나믹 프로그래밍을 이용한 대표적 최단 경로 탐색 알고리즘이다. ⇒ 최단거리는 여러개의 최단거리로 이루어짐. (특정 지점까지 거리 = A까지 가는 거리 + A에서 특정 지점까지 소요되는 거리)
따라서 특정 시작점에서 다른 모든 정점으로 가는 최단거리를 구할 수 있다.
단순하며 실행속도도 빠르다.
또한 다익스트라 알고리즘은 BFS를 이용하는 대표적인 알고리즘이다.
DFS는 한사람이 미로를 헤메는 과정이라면 BFS는 여러명이 각기 다른 갈림길로 흩어져 길을 찾는 법
다익스트라는 여러명이 갈림길이 나올때마다 흩어져 찾다가 목적지에 가장 빨리 도착한 사람의 경로를 사용하는 것으로 볼 수 있다.
그래프를 인접 리스트의 형태로 구성하면 의 시간복잡도로 구현할 수 있다.
주의
음수 가중치가 있는 그래프 에서는 다익스트라가 올바르게 동작하지 않을 수 있습니다.
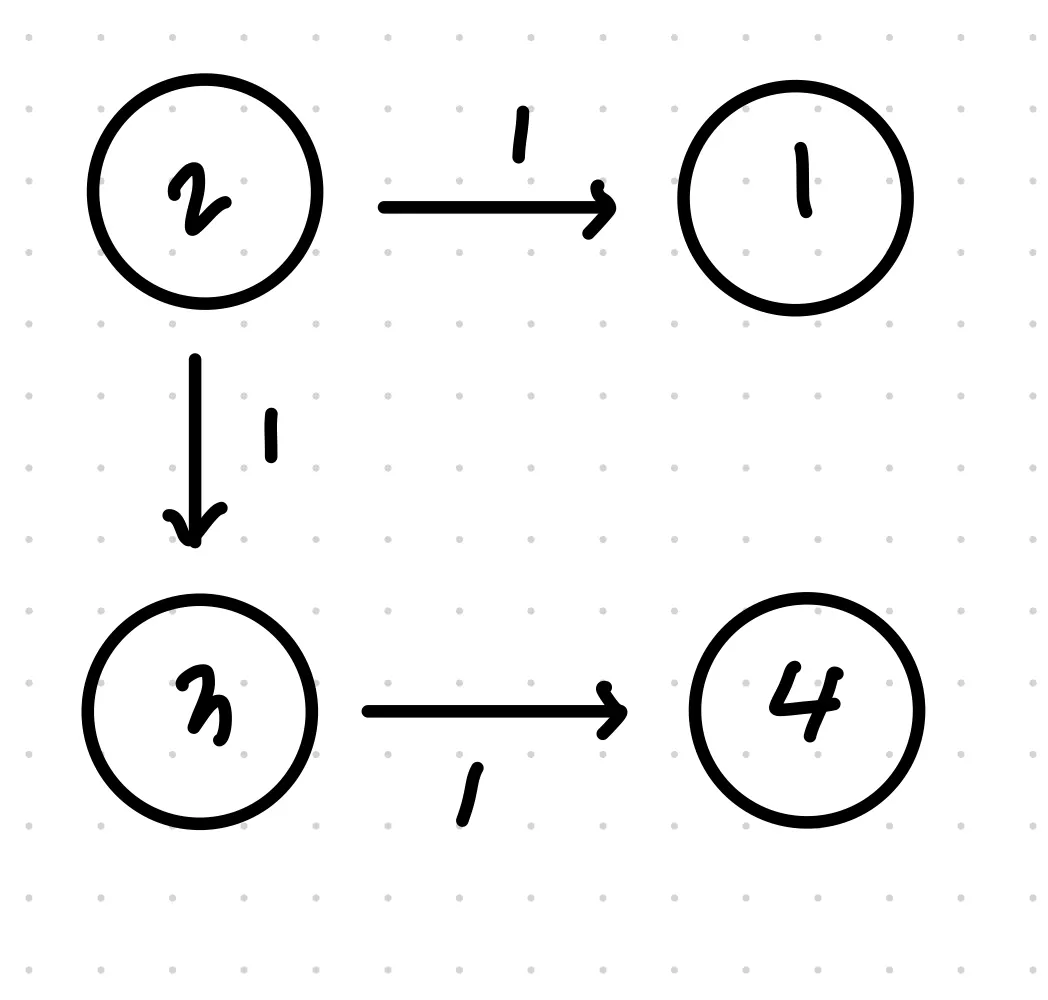
다익스트라에서는 dist중 가장 작은 값을 골랐을 때 그 값이 확실한 최단거리라는 보장이 되어야 하는데, 음수 가중치가 있으면 다시 골라졌던 정점에 도달하는 dist값이 더 작아질 수도 있기 때문에 최단거리임을 보장할 수 없게 됩니다.예제 1. 네트워크 딜레이 타임 ( 리트코드 743 )
K부터 출발해 모든 노드가 신호를 받을 수 있는 시간을 계산하라. 불가능할 경우 -1을 리턴한다. times배열안에 값들은 각각 출발지, 도착지, 소요시간 순으로 구성되며, 전체 노드의 개수는 N으로 입력받는다.
•
입력
times = [[2,1,1],[2,3,1],[3,4,1]], N = 4, K = 2
Python
복사
•
출력
2
Python
복사
이 문제는 고려해야할 사항이 두개 있다.
1.
모든 노드가 신호를 받는데 걸리는 시간
2.
모든 노드에 도달할 수 있는지 여부
1번은 소요시간이 가장 큰 노드까지의 시간이라고 볼 수 있다. 소요시간이 가장 큰 노드까지의 최단시간을 구해야 한다.
2번은 모든 노드에서의 다익스트라 알고리즘 계산값 유무로 판별 가능한데, 노드가 8개인데 계산값이 7개뿐이라면 나머지 한 노드에는 도달할 수 없는 것이기에 -1을 리턴한다.
구현
다익스트라 알고리즘은 최초의 구현과는 조금 다른 방식이지만 python에서 우선순위큐를 사용한 방식으로 구현한다.
최솟값을 골라주는 과정을 다익스트라 알고리즘에서는 여러 번 반복하게 되는데, 효과적으로 최솟값을 계속 찾아주기 위해서는 우선순위 큐를 이용해야 한다
from collections import defaultdict
import heapq
def network_delay_time(times:list, N:int, K:int):
# 그래프 생성 (그래프 인접 리스트 구성)
graph = collections.defaultdict(list)
for u, v, w in times:
graph[u].append(v, w)
# 우선순위큐 Q
Q = [(0, K)] # 처음에 소요시간은 0이고, 시작이 K노드부터이기 때문에 (0, K) 튜플로 초기화
# 각 노드에서의 최단거리를 저장할 dist
dist = defaultdict(int)
# 우선순위 큐 최솟값을 기준으로 노드까지의 최단경로(최단시간)를 삽입한다.
while Q:
time, node = heapq.heappop(Q) # Q내의 최솟값(앞에꺼기준이기떄문에소요시간(time)기준) 노드 추출
if node not in dist: # node에서의 최단거리가 연산되지 않은 상태이면
dist[node] = time
for v, w, in graph[node]: # node의 인접 노드들에 대해서
alt = time + w:
heapq.heappush(Q, (alt, v))
# 이렇게 해주면 그 다음 heappop을 수행할 때 Q에서 time 가장 낮은 노드에 대해서 수행하게 되기 때문에 계속해서 각 노드에서의 최단거리를 찾게된다.
if len(dist)==N:
return max(dist.values()) # dist는 점점 누적해가면서 time을 저장하기 때문에 가장 큰 값이 마지막 도달 지점에서의 총 걸린 시간이다.
return -1
Python
복사
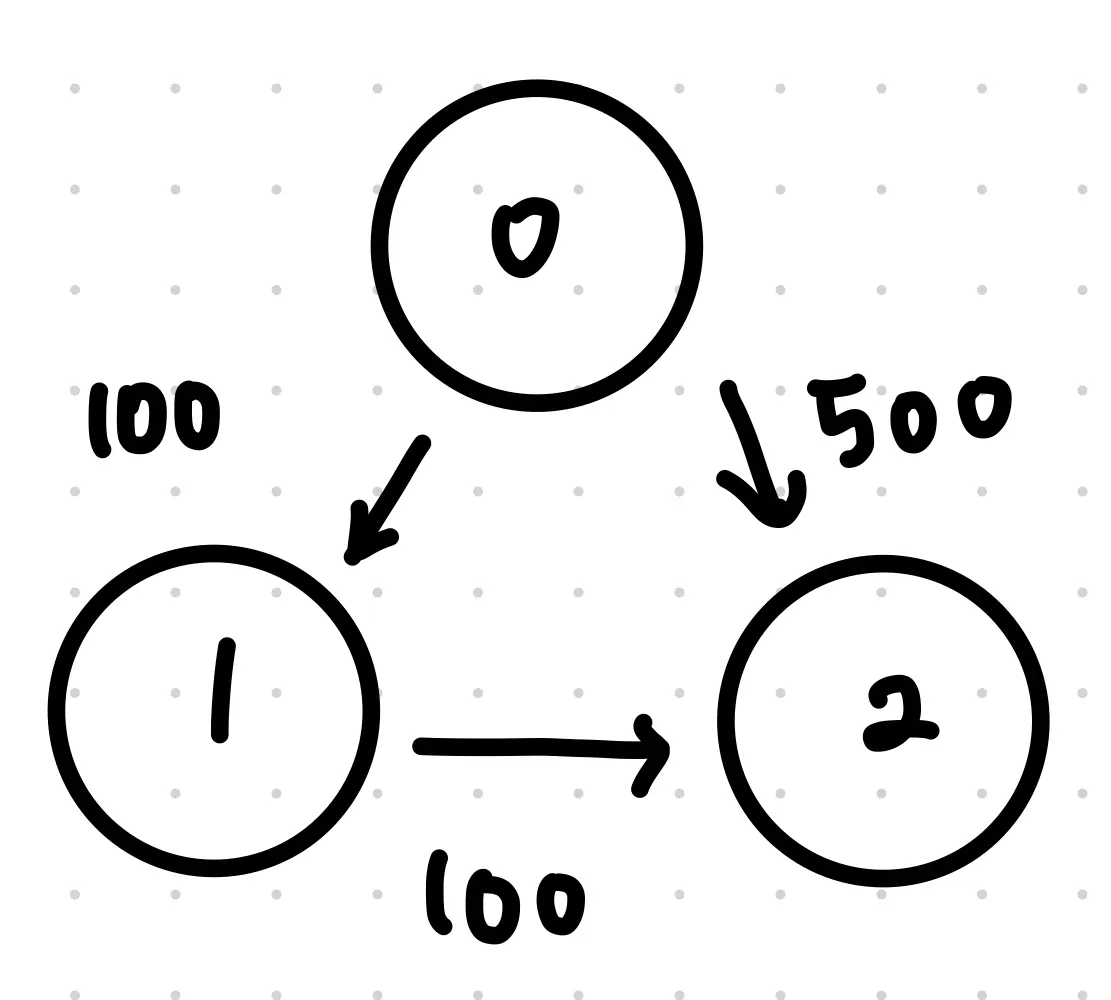
예제 2. K경유지 내의 가장 저렴한 항공권
시작점에서 도착점 까지의 가장 저렴한 가격을 계산하되, K개 경유지 내에 도착하는 가격을 리턴해라. 경로가 존재하지 않으면 -1을 리턴
•
입력
n = 3
edges = [[0, 1, 100], [1, 2, 100], [0, 2, 500]]
svr = 0, dst = 2, K=0
Python
복사
•
출력
500
Python
복사
여기서는 예제 1에서 고려햇던 최단 시간 + 경유지 개수 K를 고려해야 한다.
구현
def find_cheapest_price(n:int, flights:list, src:int, dst:int, K:int):
# 그래프 생성 (그래프 인접 리스트 구성)
graph = collections.defaultdict(list)
for u, v, w in times:
graph[u].append(v, w)
# 우선순위큐 Q
Q = [(0, src, K)] # 처음에 비용은 0이고, 시작이 src 노드부터이고 K는 남은 경유지 수 초기값으로 하여 넣어준다.
# 앞에서처럼 전체 경로 갯수 체크 단계가 필요없기 때문에 dist는 만들지 않는다.
while Q:
price, node, k = heapq.heappop(Q) # Q내의 최솟값(앞에꺼기준이기떄문에소요시간(time)기준) 노드 추출
if node == dst: # node에서의 최단거리가 연산되지 않은 상태이면
return price
if k >= 0:
for v, w, in graph[node]: # node의 인접 노드들에 대해서
alt = price + w:
heapq.heappush(Q, (alt, v, k-1)) # 하나의 노드 방문할 때마다 남은 경유지 -1해줌
# 끝까지 dst를 만나지 못하면 -1을 return 한다.
return -1
Python
복사
