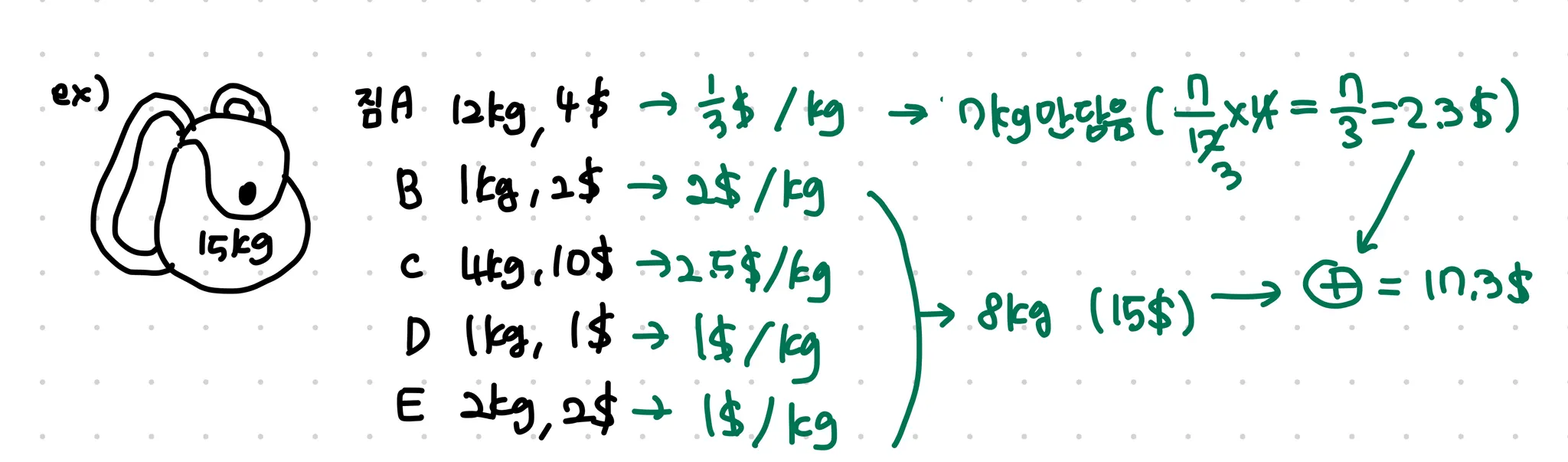Greedy algorithm (GA라 하겠다) Dynamic programming algorithm(DP라 하겠다)
두가지 알고리즘은 최적화 문제에 적용한다는 것에 있어서 유사하다. 각각을 살펴보고 다른 점을 알아보겠다.
일단 두 알고리즘은 적용하는 경우가 다르다.
Greedy | 최적 부분 구조
탐욕 선택 속성 |
Dynamic Programming | 최적 부분 구조
중복된 하위 문제들 |
이게 어떤 의미인지 각각의 알고리즘을 살펴보자
Greedy Algorithm
최적 부분 구조 ( Optimal Substruct ) 문제라는 것은 문제의 최적 해결이 부분 문제의 최적 해결인 경우를 말한다.
GA는 각 단계에서 최적 선택을 찾아가는 방법으로 전체에서의 최적해를 찾는 알고리즘이다. (휴리스틱 문제해결 알고리즘)
대부분의 경우 정답을 찾기 어려운 알고리즘이지만 합리적인 시간 내에 정답 혹은 정답에 근사한 해를 찾을 수 있어 빠르고 실용적이다.
적합 문제 예시
1.
배낭문제 ( 조합 최적화)
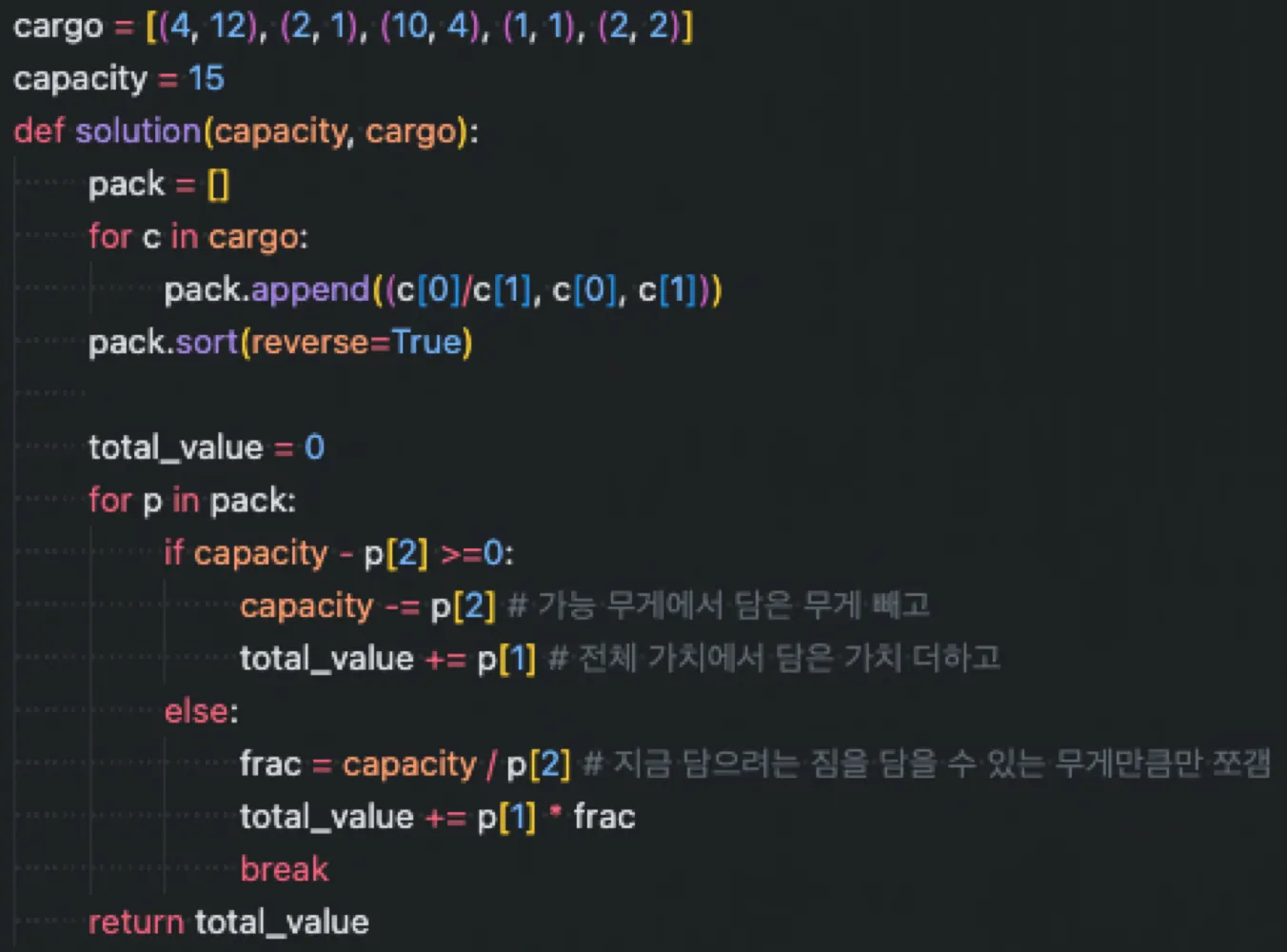
a kg을 담을 수 있는 가방과 짐들의 무게(kg), 가치($)가 주어졌을 때 가치($)가 최대가 되도록 가방에 짐을 담기.
이 문제는 두 경우로 나뉜다.
•
짐을 쪼갤 수 있는 경우 ⇒ GA 적용 : kg당 단가가 높은 것 부터 채운다
•
짐을 쪼갤 수 없는 경우 ⇒ DP 적용
a = 15이고 짐들의 무게와 가치가 (가치, 무게)의 튜플을 요소로 가지는 리스트로서 주어진다면 GA를 토왜 다음과 같이 풀이할 수 있다.
2.
동전바꾸기 문제
N원을 거슬러줄 때 가장 작은 동전 개수를 사용하는 경우 찾기
이 문제같은 경우에도 두가지 경우로 나눌 수 있다
•
10원, 50원, 100원 과 같이 이전 액면의 배수 이상이 될 때 ⇒ GA 적용
•
10원, 50원, 80원, 100원과 같이 이전 액면의 배수 이상이 되지 않을 때 ⇒ DP 적용
이 경우 큰 액수의 동전부터 순서대로 연산하면 된다.
Dynamic Programming Algorithm
DP의 경우 하나의 문제를 여러 하위문제들로 나누어 하위문제들의 결과를 문제 해결에 사용한다.
보통 점화식을 만들어 풀게 된다. 나뉘어지는 작은 경우들 (소문제들) 이 서로 독립이면서 모두 합했을 때 전체가 되어야 한다.
최적화 DP 문제에 대해서 i를 하나하나 증가시키며 i번째까지만 존재할 때 최대 or 최소를 구하기 위한 점화식을 찾는다.
•
i번째까지만 존재할 때 최댓값 : dp[n]
•
i번째까지만 존재하면서 i번째 고를 때 최댓값 : max(dp)
적합 문제 예시
피보나치 수열이 매우 기본적인 문제이기 때문에 이를 사용해 DP의 예시를 살펴본다.
DP의 방법론은 두가지로 나누어진다.
•
하향식 접근법 : memoization
하위 문제에 대한 정답을 계산했는지 확인해가며 문제를 자연스러운 방식으로 풀어나간다.
이미 계산한 값은 저장해두기에 매우 효율적인 방법이다.
•
상향식 접근법 : tabulation
더 작은 하위 문제부터 살펴본 후 작은 문제의 정답을 이용해 큰 문제의 정답을 풀이한다.
일반적으로 이 방식만을 DP라고 지칭하기도 한다.
순차적으로 저장해가며 반복구조로 수행하여 직관적이고 이해가 쉬우며 실행시간도 역시 빠르다