Search

조건부확률과 Bayes 정리

※ KOCW 이상화교수님의 확률 및 통계 강좌를 기반으로 정리한 내용입니다

정의 살펴보기

•
Sample space (S) : 시행 결과가 완전히 랜덤할 때, 시행의 모든 가능한 결과들의 집합
•
Event (A) : sample space의 부분 집합. (A⊂SA \sub S)
◦
P(A) : A라는 event가 발생할 확률
◦
sample space에서 하나의 결과를 뽑았을 때 이 결과가 A에 속할 확률 (outcome∈Aoutcome \in A 일 확률)
•
조건부확률 (conditional probability)
: P(B|A) 와 같이 표현하며 이는 A라는 condition이 발생했을 때 B라는 event가 발생할 확률을 의미한다.
P(B∣A)=P(B∩A)P(A)=P(B∩A∣S)P(A∣S)P(B|A) = \frac{P(B \cap A)}{P(A)} =\frac{P(B\cap A|S)}{P(A|S)}
위와 같이 나타낼 수 있으며 마지막 식에서 나타냄과 같이 어떤 sample space가 항상 조건으로 주어진다. 그러나 sample space 외에는 고려할 필요가 없으므로 생략하여 나타낸다.
•
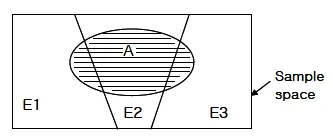
total probability : 특정 경우 ( e.g. event A ) 의 확률. P(A)와 같이 나타낸다.
◦
sample space S는 {E1, E2, …, En} n개의 배반사건으로 나눌 수 있다. ⇒ E1, E2, E3, …, En은 S의 부분집합.
◦
따라서 P(A)는 다음과 같이 나타낼 수 있다. P(A)=P(E1∩A)+P(E2∩A)+…+P(En∩A)=P(A∣E1)P(E1)+P(A∣E2)P(E2)+...+P(A∣En)P(En)=∑i=1nP(A∣Ei)P(Ei)P(A) = P(E_1 \cap A) + P(E_2 \cap A) + … + P(E_n \cap A)\\=P(A|E_1)P(E_1) + P(A|E_2)P(E_2)+... + P(A|E_n)P(E_n) \\= \sum_{i=1}^nP(A|E_i)P(E_i)
◦
이에 대한 역도 성립한다.
◦
P(A∣Ei)P(A|E_i) 는 priori(사전확률)이라고 할 수 있다.

Bayesian theorem

P(B∣A)=P(B∩A)P(A),        P(A∣B)=P(A∩B)P(B)P(B|A) = \frac{P(B \cap A)}{P(A)} ,\;\;\;\; P(A|B) = \frac{P(A \cap B)}{P(B)}
P(B∣A)=P(A∣B)  P(B)P(A) P(B|A) = \frac{P(A|B)\;P(B)}{P(A)}
위 식이 베이즈 정리이다.
이를 통해 위에서 A와 A내의 배반사건 Ai에 대해 A에 대한 Ai의 조건부확률을 다음과 같이 나타낼 수 있다.
P(Ai∣A)=P(A∣Ai)P(Ai)P(A)P(A_i|A) = \frac{P(A|A_i)P(A_i)}{P(A)}
여기서 A는 이미 관측한 데이터, 즉 observation data라고 할 수 있고, AiA_i는 input data / original data / unseen data라고 할 수 있다. 이에 대한 예시로 Binary Symmetric channel 예시를 알아본다.

ex) Binary Symmetric Channel

input symbols : {x1x_1, x2x_2}
output symbols : {y1y_1, y2y_2}
binary이기 때문에 x1=0,x2=1,y1=0,y2=1x_1=0, x_2=1, y_1 = 0, y_2=1로 보아도 무관하다.
receiver에서 받는 것은 output symbols이기에 output symbols를 observation data라고 할 수 있다.
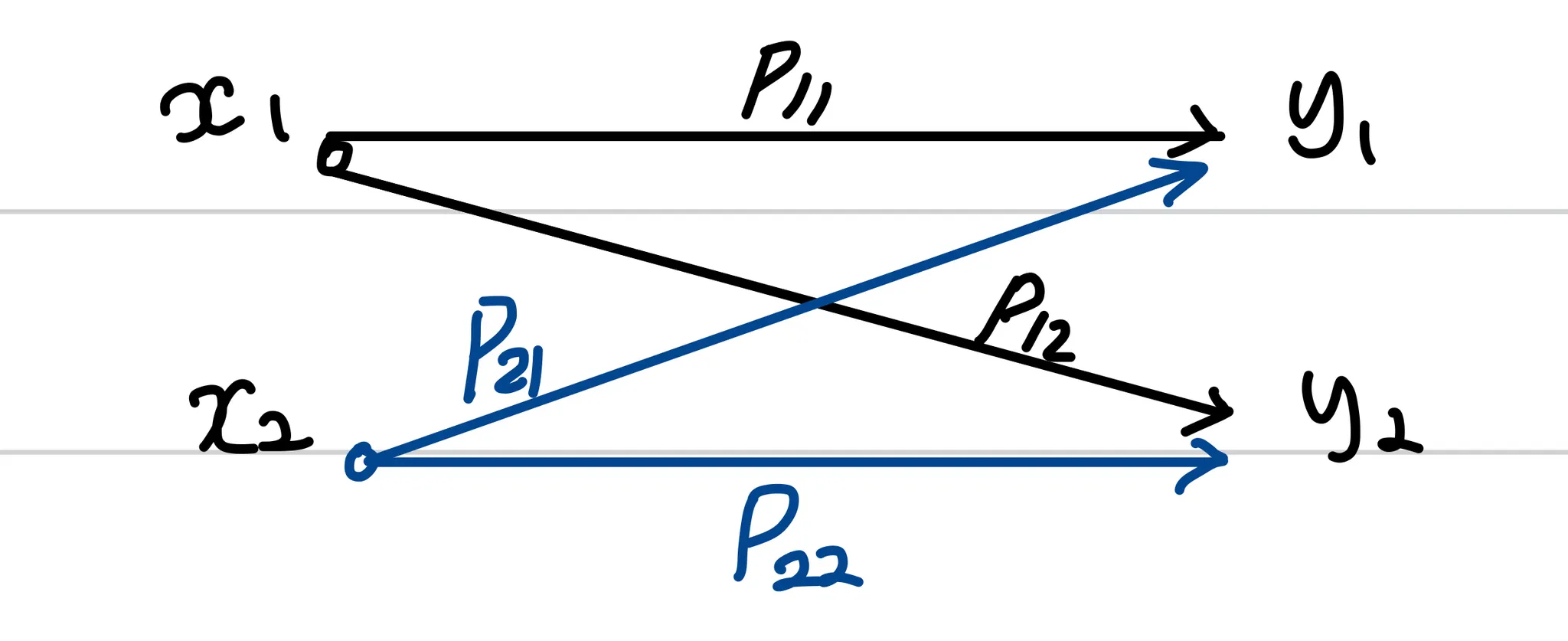
x1x_1을 전송해 y1y_1을 받고, x2x_2를 전송해 y2y_2를 받는 것이 이상적이지만, 현실은 그렇지 못하다. 확률이라는 것이 존재한다.
PijP_{ij} = xix_i가 전송되었을 때 yiy_i를 받을 확률이며
binary symmetric channel의 경우 P11=P22,  P12=P21P_{11} = P_{22}, \; P_{12}=P_{21}이다.
이를 조건부확률 식으로 나타내면
P11=P(y1∣x1)P_{11} = P(y_1|x_1)
P22=P(y2∣x2)P_{22} = P(y_2|x_2)
P12=P(y2∣x1)P_{12} = P(y_2|x_1)
P21=P(y1∣x2)P_{21} = P(y_1|x_2)
이 외에 P(x1x_1)과 P(x2x_2) 까지가 priori라고 할 수 있다.
※ 여기서 P11+P12P_{11} + P_{12} = 1, P22+P21=1P_{22} + P_{21} = 1
Q1. transmission 환경에서 error가 발생할 확률
이는 x1x_1을 전송했는데 y2y_2를 받는 경우의 확률과 x2x_2를 전송했는데 y1y_1을 받을 확률의 합으로 나타낼 수 있다.
prob(x1전송,y2수신)+prob(x2전송,y1수신)=P(y2∣x1)P(x1)+P(y1∣x2)P(x2)prob(x_1 전송,y_2수신) + prob(x_2전송, y_1수신) \\ = P(y_2|x_1)P(x_1) + P(y_1|x_2)P(x_2)
이는 어떠한 조건 없이 그냥 에러가 발생할 확률이기 때문에 unconditioned error의 확률이라고 한다.
Q2. y2y_2가 수신되었을 때 x1x_1이 송신되었을 확률
⇒ P(x1∣y2)P(x_1|y_2)
여기서 y2y_2를 observation data라고 할 수 있고, condition이다.
P(x1∣y2)=P(y2∣x1)P(x1)P(y2)=P(y2∣x1)P(x1)P(x1∣y2)P(x1)+P(x2∣y2)P(x2)P(x_1|y_2) = \frac{P(y_2|x_1)P(x_1)}{P(y_2)}=\\ \frac{P(y_2|x_1)P(x_1)}{P(x_1|y_2)P(x_1)+P(x_2|y_2)P(x_2)}
이렇게 priori를 가지고 확률을 계산해낼 수 있다.
Q3. error가 발생했을 때 x1x_1을 송신하였을 확률
⇒ P(x1∣error)P(x_1|error)
P(x1∣error)=P(error∣x1)P(x1)P(error)=P(y2∣x1)P(x1)P(y1∣x2)P(x2)+P(y2∣x1)P(x1)=P(x_1|error) = \frac{P(error|x_1)P(x_1)}{P(error)}=\frac{P(y_2|x_1)P(x_1)}{P(y_1|x_2)P(x_2)+P(y_2|x_1)P(x_1)}=

독립 (independent)

event A와 event B가 (mutually) independent 하다는 것은 다음과 같이 정의된다.
P(B∣A)≜P(B)P(A∣B)≜P(A)P(B|A)\triangleq P(B)\\P(A|B) \triangleq P(A)
즉 A와 B가 서로의 확률에 영향을 미치지 않는다는 것이다. 이를 조건부 확률의 식으로 정리하면 다음과 같다.
P(B∣A)=P(A∩B)P(A)=P(B)P(A∣B)=P(A∩B)P(B)=P(A)P(B|A) = \frac{P(A \cap B)}{P(A)} = P(B)\\ P(A|B) = \frac{P(A \cap B)}{P(B)} = P(A)
이를 통해 다음이 도출된다
P(A∩B)=P(A)P(B)P(A\cap B) = P(A)P(B)
즉 P(A∩B)=P(A)P(B)P(A\cap B) = P(A)P(B) 이면 A와 B는 독립하다고 할 수 있다.

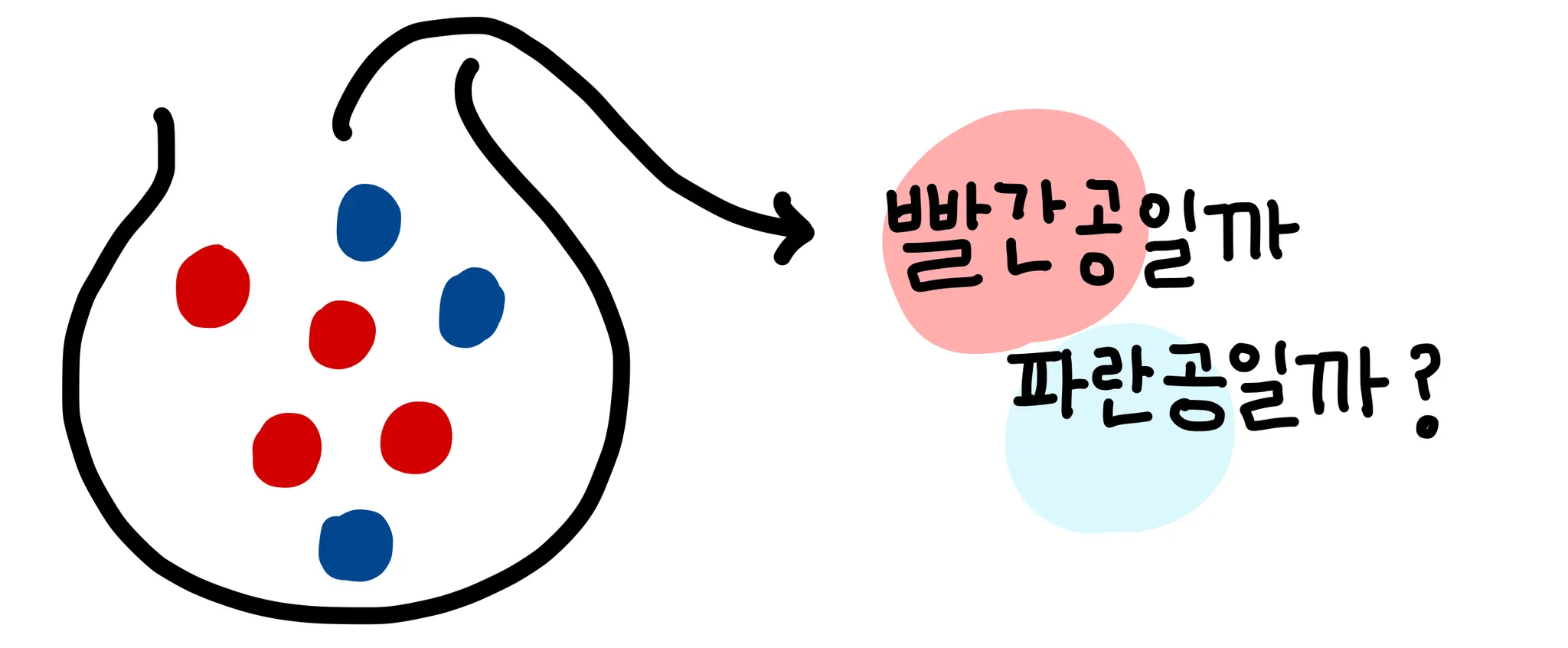
ex) 복원 추출 반복 시행 (repeated restored trials)

그림과 같이 어떤 주머니에 빨간공과 파란공이 들어있다고 하자. 공을 뽑은 다음 다시 집어넣는 과정을 반복하면 각 추출시에 공이 빨간 공일 확률과 파란공일 확률은 일정하다.
즉, 앞의 시행 결과가 뒤의 시행 결과에 영향을 미치지 않는다. ⇒ independent
이와 같이 독립이라는 조건은 확률적인 문제를 쉽게 만들어 준다. 조건부 확률이 필요없어지기 때문이다.

독립 가정을 통해 현실의 확률적 모델링을 단순화하기

예를 들어 오늘의 날씨를 모델링한다고 생각하자.
오늘의 날씨를 WtW_t라고 한다면 오늘의 날씨에는 어제의 날씨, 이틀 전의 날씨, ….., n일 전의 날씨가 모두 영향을 미칠 것이다. 그러면 다음과 같이 표현된다.
P(Wt∣Wt−1,Wt−2,...,Wt−n)P(W_t|W_{t-1}, W_{t-2}, ..., W_{t-n})
n은 아주 무수한 숫자가 될 것이다. 그러나, 1년 전의 날씨가 오늘의 날씨에 미치는 영향은? 거의 없을 것이다. 이러한 요소들을 모두 독립 취급하여 이틀 전의 날씨까지만 오늘의 날씨에 영향을 미친다고 하면, 다음과 같이 단순화된다.
P(Wt∣Wt−1,Wt−2)P(W_t|W_{t-1}, W_{t-2})
또 다른 예시를 들자면 서울의 날씨를 계산할 때 뉴욕의 풍속을 인자로 두지는 않는다. 즉, 서울의 날씨와 뉴욕의 풍속은 독립으로 취급된다.

combined experiments (여러 실험의 조합)

만약 두개의 실험이 있고, 각 실험에 대한 sample space를 S1,S2S_1, S_2라고 한다면, combined sample space는 다음과 같이 표현된다.
S=S1×S2={(xi,yj)∣xi∈S1,yj∈S2}S = S_1 \times S_2 = \{ (x_i, y_j)|x_i \in S_1, y_j \in S_2\}
여기서 ×\times 는 cartesian product이다. (각 집합의 원소를 각 성분으로 하는 튜플들의 집합)

ex) 3 개의 동전 던지기

1개의 동전던지기 실험 3개가 합쳐진 것이다.
S1={H,T},S2={H,T},S3={H,T}S_1 = \{H, T\}, S_2 = \{H, T\}, S_3 = \{H, T\}
S=S1×S2×S3={HHH,HHT,…,TTH,TTT}S = S_1 \times S_2 \times S_3 = \{ HHH, HHT, …, TTH, TTT\}
Made with