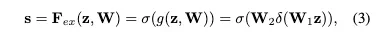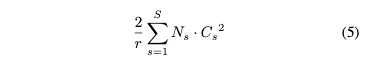💗

[SENet] Squeeze-and-Excitation Networks ( CVPR 2018 )

Abstract

CNN 의 convolution 연산 : local receptive field 내에서 spatial and channel-wise 정보들을 함께 fusing해 informative features를 추출

이 논문 이전의 다양한 접근에서 spatial encoding을 향상시키는 것의 장점에 대해 보여줬지만 (현재는 channel attention에 대한 논문이 많이 나오고 있다 )이 논문에서는 채널간의 관계에 집중해 새로운 아키텍쳐 유닛인 Squeeze-and-Excitation block ( SE block )을 제안한다

SE block은 채널간의 interdependencies를 명확히 모델링함으로써 chnnel-wise 피쳐들을 recalibrate 한다

이 block을 쌓아 어려운 데이터셋들을 잘 일바노하하는 아키텍쳐를 만들 수 있다

작은 computational cost의 추가만으로 SOTA deep architecture의 성능을 높였다

Introduction

conv레이어들의 필터들은 input channels 들 사이에서 local spatial connectivity를 학습한다

convolution filter들은 해당 receptivd field내에 spatial한 정보와 channel-wise정보를 함께 fusing한 informative combinations로 예측가능하다

또한 CNN은 깊을수록 강력한 image descriptions로 작동

최근 spatial correlations를 추가적 supervision없이 더 잘 감지할 수 있도록 메커니즘 연구가 많이 있었으며 그 중 하나가 Inception Architecture다

이 논문에서는 channel relationship에 집중한 아키텍쳐 디자인을 제안하며 SEblock을 제안한다

Our goal is to improve the rep- resentational power of a network by explicitly modelling the interdependencies between the channels of its convolu- tional features.

feature recalibration을 통해 global information을 사용하도록 학습 ( informative features는 강조하고 less useful한 features는 억제 ) → 피쳐맵 채널간의 상호연관성을 명확히 모델링 → 네트워크의 representational power 향상

SENet 장점

아키텍쳐의 어떠한 depth에든 끼워넣을 수 있다

그러나 레이어의 depth별 역할이 다르기 때문에 주의가 필요하다 (section6.4에 자세한 설명 있음)

•

early layer : 이 레이어들은 피쳐채널들의 중요성을 클래스들간에 공유하기 때문에 (i.e. 2, 3, 채널이 class 0, 1, 2모두에게 중요할 수 있음  ) ( 좀 더 일반화된 피쳐들 ) 
SEblock을 여기에 끼워넣으면 클래스에 관계 없이 informative features를 강조하기 때문에  shared lower level represetation의 quality 강화

•

later layer : 이 레이어들은 피쳐 채널들의 중요성이 클래스별로 다른 경향을 보인다. 
SEblock을 여기에 끼워넣으면 좀 더 specialised하게 된다 input들에게 class specific하게 대응한다.

•

그러나 거의 마지막에 가까운 레이어에서의 SEBlock은 피쳐 recalibration에 거의 필요하지 않는다고 한다( fig 5 의 실험 )

1 - 2 . 따라서 현존하는 SOTA 모델들에 바로 적용이 가능하다 → 기존 모듈 강화의 역할

light weight를 가지는 block으로, 성능향상에 비해 매우 적은 모델 복잡도와 계산 복잡도 만이 더해진다

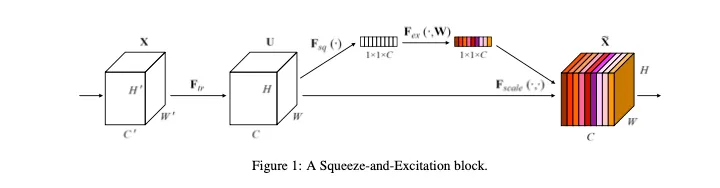
Squeeze-and-Excitation Blocks

Squeeze : Global Information Embedding

F_{tr} : X \rightarrow U,\; X \in \mathbb{R}^{H’ \times W’ \times C’},\; U \in \mathbb{R}^{H\times W \times C}

U=[u_1, u_2, …., u_C], \; v_C=[v_c^1, v_c^2, ..., v_c^{C'}], \; X=[x^1, x^2, ..., x^{C'}]

v_c^s

는 2차원 kernel로,

그냥 bias 없는 convolution 연산이라고 볼 수 있다

식을 보면 채널방향 sum으로 되어있기 때문에, 채널간 상관성이

v_c

에 임베딩되게 된다. 그러나 필터 내에서 캡쳐된 spatial correlation과 entangled (얽혀있음 ) 상태이다.

그림의

F_{sq}

결과인 1x1xC 는 stastic

z

이다

F_{sq}

는 Global Average Pooling(GAP)이다

Excitation : Adaptive Recalibration

Squeeze 단계에서 통합된 정보를 사용하기 위한 단계이다.

channel-wise dependencies를 완전히 잡아내기 위해 이 함수는 두가지 기준이 필요하다.

flexible해야한다

채널간의 nonlinear한 상호작용까지도 학습할 수 있어야 한다.

non-mutually-exclusive( 상호배타적이지않은) 관계를 배워야한다. 

왜냐하면 다양한 채널들이 강조되도록 하고싶기 때문이다 ( one hot encoding과 다르게 )

이 조건들을 만족시키기 위해 sigmoid activation과 함꼐 simple gating mechanism을 적용했다.

이후

F_{ex}

는 W1, W2로 정의된 MLP를 겨치게 되는데

이러한 형태를 띄며 W1 이후

\delta

로 정의된 ReLU를 거친다

모델 복잡도를 제한하고 일반화를 하기 위해 MLP 형태를 적용했다고 한다

r은 reduction rate로 실험적으로 16으로 정했다고 한다

W_1 \in \mathbb{R}^{\frac{C}{r} \times C}, W_2 \in \mathbb{R}^{ C \times \frac{C}{r}}

이 block의 output은 convolution연산으로 나왔던

U

와

F_{ex}

의 결과인

s

의 chnnel-wise multiplication이다

SE-Inception SE-ResNet

Model and Computational Complexity

SE block의 파라미터는 두개의 FC 레이어의 파라미터 수 만큼이므로

FC 레이어 하나당 파라미터 =

\frac{2}{r}\times C \times C = \frac{2}{r}C^2

N_s

= stage s에서 반복된 block 수

C_s

= output channel 수

S

= stage 수

수식(5)만큼의 파라미터 수가 증가하게 된다

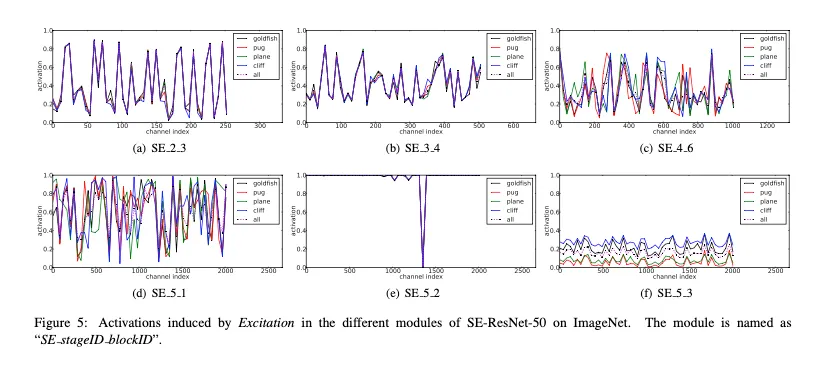
The Role of Excitation

•

validation set의 4가지 클래스에 대해서 50개의 sample의 activations에 대한 평균값을 그린 그래프다.

SE.2.3, 이나 SE.3.3같은 early layer는 4가지 클래스에 대해 거의 같은 값을 갖는다

→ 더 글로벌한 피쳐가 나오는 레이어이기 때문에 대부분의 클래스에서 중요한 채널이 비슷하다는 것

SE4.6.이나 SE5.1을 보면 클래스별로 다른 값을 보인다.

→ 좀 더 class-specific한 피쳐가 나온다는 뜻이다

따라서 두 경우 SE의 역할은 다르다

그러나 SE_5.2, SE_5.3이라는 classifier에 들어가기 직전인 마지막 레이어들의 SE를 보면,

•

5.2같은 경우 거의 1이고 한 값만 0이라서 거의 SE의 역할이 적용되지 않고, 

•

5.3같은 경우에는 scale을 제외하면 거의 같은 모양을 보여 효과가 적다

⇒ 따라서 마지막 스테이지의 SE 블록을 없애는 것이 성능 손해를 거의 보지 않고 파라미터 수를 줄일 수 있다.