Search

Exponentially Weighted Averages ( 지수 가중 평균 ) ( Exponentially weighted moving averages )

데이터의 이동 평균을 구할 때,오래된 데이터가 미치는 영향을 지수적으로 감쇠(exponential decay) 하도록 만들어 주는 방법.
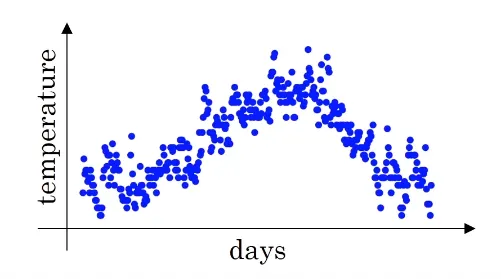
Exponentially Weighted Averages (C2W2L03)
https://www.youtube.com/watch?v=lAq96T8FkTw&list=LLypIXWIsUMIMvCa6zQfOZmQ&index=14

(예시) Temperature in London

θ1=40∘F\theta_1 = 40^{\circ}F
θ2=49∘F\theta_2 = 49^{\circ}F
θ3=45∘F\theta_3 = 45^{\circ}F
…
θ180=60∘F\theta_{180} = 60^{\circ}F
θ181=56∘F\theta_{181} = 56^{\circ}F
…
이 데이터의 시간의 흐름에 따른 변화를 그리고싶다면 어떻게 해야할까?
V0=0V_0 = 0으로 정의하고,
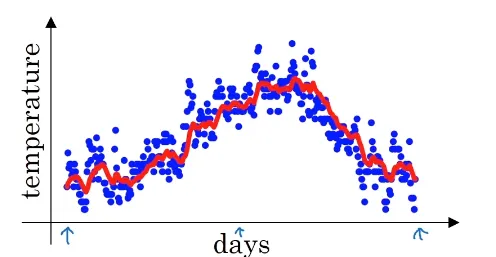
Vt=0.9×Vt−1+0.1×θtV_t = 0.9 \times V_{t-1} + 0.1 \times \theta_t 이라고 정의해 이를 그래프로 그리면
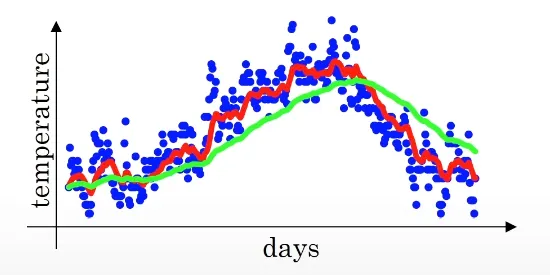
위의 빨간 선과 같다. 이런 방식이 지수 가중 평균이다.
0.9를 β\beta로 표기하면
Vt=β×Vt−1+(1−β)×θtV_t = \beta \times V_{t-1} + (1-\beta) \times \theta_t
이렇게 식을 정의할 수 있다.
이때 β\beta 는 0~1 사이의 값을 갖는 하이퍼파라미터이고, θ\theta는 새로 들어온 데이터라고 생각하면 된다.
VV는 현재의 경향을 나타내는 값이라고 이해하자.
왼쪽의 Vt−1V_{t-1} 부분은"과거의 경향성"이고,+ 이후의 (1-β) * θ\theta는 새로운 경향성을 나타내기 위해 새로 들어온 데이터를 반영하는 (최신의 기온을 평균 산식에 넣어주는) "새로운 경향성" 이라고 이해할 수 있다.
VtV_t 는 대략적으로 1(1−β)×일별기온\frac{1}{(1-\beta)} \times 일별 기온 의 평균과 같다.
이유
β=0.9\beta = 0.9 이면 VtV_t 는 10일간의 기온의 평균과 유사한 것이다.
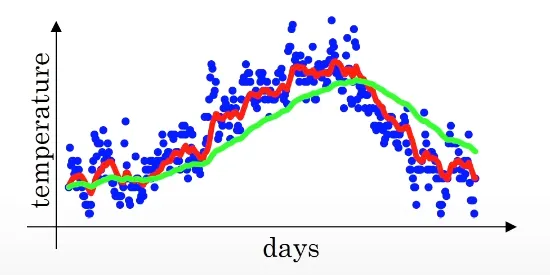
β=0.98\beta = 0.98 이면 VtV_t는 50일간의 기온의 평균과 유사해지고 아래 그래프의 초록색 선과 같아진다
더 많은 날짜의 기온의 평균을 이용하기 때문에 초록색 선이 비교적 좀 더 부드럽다.
다르게 말하면, 기온의 변화에 더 느리게 적응하게 된다. 따라서 날씨 예측에 더 지연이 생기게 된다.
이유를 생각해보면, β=0.98\beta = 0.98 로 크게 적용시키면, 이전 값에 더 큰 가중치를 주고 현재 기온에 더 작은 가중치를 주게된다. 그래서 온도가 상승하면 더 느리게 적응하게 된다.
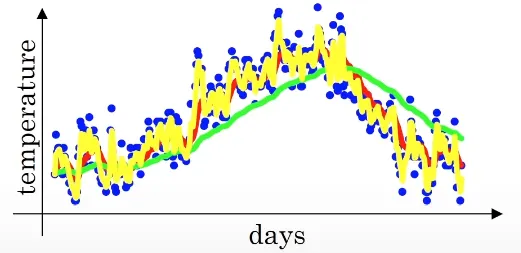
아예 반대의 극단적인 예시로β=0.5 \beta=0.5라면? → 2일간의 평균만 이용하게 되고 아래의 노란 그래프와 같아진다
확실히 기온 변화에 빠르게 적응하지만, 이상치에 민감하고 noise가 더 많아진다
이제 이 공식을 V100V_{100}을 구하고, β\beta가 0.9라는 가정으로 나열해보면
V100=0.1θ100+0.9(0.1θ99+0.9(0.1θ98+0.9V97)=0.1θ100+0.1×0.9×θ99+0.1(0.9)+0.1(0.9)2θ98+0.1(0.9)2θ97+.....V_{100} = 0.1\theta_{100}+ 0.9(0.1\theta_{99}+0.9(0.1\theta_{98}+0.9V_{97})=0.1\theta_{100}+0.1 \times 0.9 \times \theta_{99} + 0.1(0.9) + 0.1(0.9)^2\theta_{98} + 0.1(0.9)^2\theta_{97}+ .....
이렇게 된다. “지수적으로(exponentially)" 감소하는 모습을 볼 수 있다
( θ\theta 값들 앞에 곱해지는 계수들을 모두 더하면 1 혹은 1에 가까운 값이 되는데, 이를 bias correction이라고 할 수 있다고 한다. )
이렇게 되기때문에 만약β=0.9 \beta = 0.9 라면 10일 뒤에는 가중치가 현재 가중치의 0.910≈0.350.9^{10} \approx 0.35 배정도로 줄어든다
보통 V_0 = 0으로 초기화하고
V0=0V_0=0
V1=βV0+(1−β)θ1V_1=\beta V_0 + (1-\beta) \theta_1
V2=βV1+(1−β)θ2V_2=\beta V_1 + (1-\beta) \theta_2
V3=βV2+(1−β)θ3V_3=\beta V_2 + (1-\beta) \theta_3
…
가장 최근의 값만 저장하면 되므로 매우 단순하고 하나의 실수를 저장하는 메모리만 필요하다
→ 한 줄의 코드만 필요

bias correction

bias correction을 통해 평균을 더 정확히 계산할 수 있다.
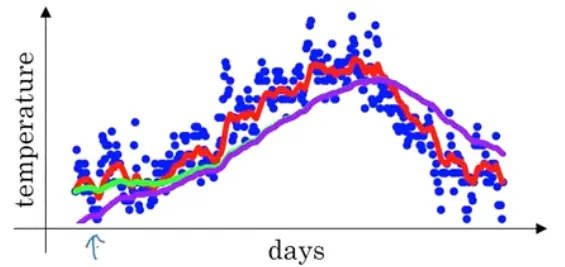
원래 위에서β=0.98 \beta = 0.98일 때 초록색 곡선을 얻을 수 있을 것이라고 했는데,
vt=βt−1+(1−β)θtv_t=\beta_{t-1}+(1-\beta) \theta_t 이렇게 구현하면 초록 곡선을 얻을 수 없다.
더 낮은 곳에서 출발하는 보라색 곡선을 얻게된다.
이를 고치려면 bias correction이 필요하다.
β=0.98\beta = 0.98 일 때
v0=0v_0 = 0
v1=0.98  v0+0.02  θ1=0+0.02  θ1=0.02  θ1v_1 = 0.98 \; v_0 + 0.02 \; \theta_1 = 0 + 0.02 \; \theta_1 = 0.02 \; \theta_1
v2=0.98  v1+0.02  θ2=0.98×0.02×θ1+0.02  θ2=0.0196  θ1+0.02  θ2v_2 = 0.98 \; v_1 + 0.02 \; \theta_2 = 0.98 \times 0.02 \times \theta_1 + 0.02 \; \theta_2 = 0.0196 \; \theta_1 + 0.02 \; \theta_2
θ1,θ2\theta_1, \theta_2가 양수라면 v_2의 값은 θ1,θ2\theta_1, \theta_2보다 매우 작아진다
처음 두개의 예측값이 매우 안좋아질 수 있는 것이다.
특히 이 초반의 추정값을 더 낫게 하는 것이 bias correction이다.
vtv_t대신 vt1−βt\frac{v_t}{1-\beta^t} 를 취하는 것이다.
ex) t=2 :1−βt=1−(0.98)2=0.0396,    v2/0.0396=0.0198θ1+0.02θ2/0.0396 1-\beta^t = 1-(0.98)^2 = 0.0396, \;\;v2/0.0396 = 0.0198 \theta_1 + 0.02 \theta_2 / 0.0396
⇒ θ1\theta_1과 θ2\theta_2 의 weighted average에 bias를 없앤 값이라고 할 수 있다.
⇒ t가 커질수록 βt\beta^t는 0에 가까워진다 ⇒ t가 충분히 커지면 bias correction의 효과는 사라진다
⇒ 보라색 선에서 초록색 선에 가까워진다.
Made with