삽입정렬 Insertion Sort
삽입 정렬(揷入整列, insertion sort)은 자료 배열의 모든 요소를 앞에서부터 차례대로 이미 정렬된 배열 부분과 비교하여, 자신의 위치를 찾아 삽입함으로써 정렬을 완성하는 알고리즘이다 (위키백과 )
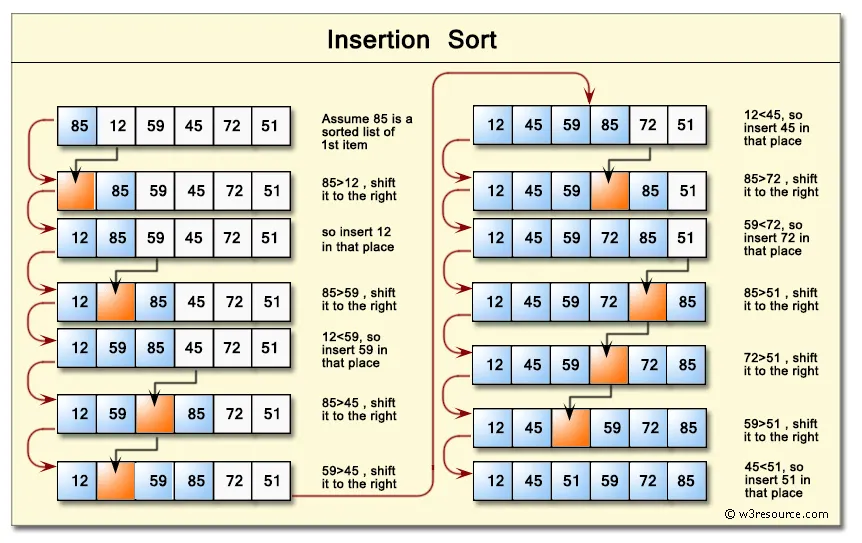
사진으로 설명해보자면,
1.
첫번째 인덱스 값인 85를 정렬된 배열(오름차순)의 첫번째 값으로 보고 다음요소(12)로 이동
2.
이전 인덱스 값들과 비교해 이전 요소가 더 큰 값이 있다면 교환(swap)하는 방식이다
3.
그러므로 85>12이기 때문에 85와 12를 swap
4.
그 다음 요소인 59
5.
59<85이므로 swap
6.
59>12이므로 swap하지 않고 12, 59, 85, ... 의 순이 된다
7.
다음요소 45
8.
45<85이므로 swap
9.
45<59이므로 swap
10.
45>12이므로 그대로 → 12, 45, 59, 85, ... 순이 된다.
11.
이것을 마지막 요소까지 반복하면 12, 45, 51, 59, 72, 85로 오름차순 정렬이 된다.
크기에 따라 새로운 인덱스에 값을 삽입하는 형태
[구현 1]
void InsertionSort(int list[], int n){
int i, j, key;
// 인텍스 0은 이미 정렬된 것으로 볼 수 있다.
for(i=1; i<n; i++){
key = list[i]; // 현재 삽입될 숫자인 i번째 정수를 key 변수로 복사
// 현재 정렬된 배열은 i-1까지이므로 i-1번째부터 역순으로 조사한다.
// j >= 0 이어야
// key 값보다 정렬된 배열에 있는 값이 크면 j번째를 j+1번째로 이동
j = i;
while (list[j-1] > key)
list[j] = list[j-1]; j--;
if (j==0) break;
list[j] = key;
}
}
C
복사
[구현 2]
void InsertionSort(int A[ ], int n)
/* 입력: A[0:n] , n: 원소의 개수. A[0]: dummy.
출력: A[0:n] : A[0]: dummy, A[1:n]은 정렬된 배열임
*/
// A[0]은 dummy -> 마이너스 무한대로 가정, A[1]은 이미 정렬됐다고 봄
{ int i, j, Value;
for (i = 2; i <= n; i++) { // A[2]부터 반복문 실행
Value = A[i];
j = i;
while (A[j-1] > Value)
A[j] = A[j-1]; j--; // 한 칸씩 땡겨오는 느낌
A[j] = Value;
}
}
C
복사
•
i, j, value 등 상수크기의 메모리를 사용하므로 제자리 정렬
•
인접한 레코드끼리만 자리를 바꾸게 되므로 안정성 충족. 안정된 정렬
•
아예 역순으로 정렬되어 있는 레코드의 경우 i번째 키를 삽입하면 i번의 비교를 수행해야 하므로
2 + 3+ 4+... + n = n(n+1)/2-1 이므로
의 최악 시간복잡도를 가진다
•
이미 정렬된 레코드는 n-1번 비교하므로 최선 시간복잡도는 이다
•
평균시간복잡도는
A[1 : i-1]에 A[i] 삽입시
◦
평균 비교 횟수 =
◦
평균 시간 복잡도 =
평균시간복잡도는 로 다소 비효율적으로 보일 수 있는 정렬 방법이지만, 이미 정렬이 되어있거나 혹은 많은 부분이 이미 정렬이 되어있을 때, 일부 요소를 삽입만 하는 경우에는 실제 복잡도는 을 갖게되는 아주 효율적인 정렬 방법이다.
쉘 정렬
•
삽입 정렬은 입력되는 초기리스트가 "거의 정렬"되어 있을 경우 효율적이다.
•
삽입 정렬은 한 번에 한 요소의 위치만 결정되기 때문에 비효율적이다.
셸 정렬은 주어진 자료 리스트를 특정 매개변수 값의 길이를 갖는 부파일(subfile)로 쪼개서, 각 부파일에서 정렬을 수행한다.
즉, 매개변수 값에 따라 부파일(Subfile)이 발생하며, 매개변수값을 줄이며 이 과정을 반복하고 결국 매개변수 값이 1이면 정렬은 완성된다.
셸 정렬은 다음과 같은 과정으로 나눈다.
1.
데이터를 십수 개 정도 듬성듬성 나누어서 삽입 정렬한다.
2.
데이터를 다시 잘게 나누어서 삽입 정렬한다.
3.
이렇게 계속 하여 마침내 정렬이 된다.
셸 정렬에서 데이터를 나누는 값(이하 N)은 보통 전체에서 2로 나누는 값으로 진행한다. 그러나 3을 나누고 1을 더하는 경우가 더 빠르다고 알려져 있다. 즉 N/2 보다는 N/3+1이 더 빠르다.
좀 더 쉽게 과정을 설명하자면
1.
먼저 정렬해야 할 리스트를 일정한 기준에 따라 분류
2.
연속적이지 않은 여러 개의 부분 리스트를 생성
3.
각 부분 리스트를 삽입 정렬을 이용하여 정렬
4.
모든 부분 리스트가 정렬되면 다시 전체 리스트를 더 적은 개수의 부분 리스트로 만든 후에 알고리즘을 반복
5.
위의 과정을 부분 리스트의 개수가 1이 될 때까지 반복
구체적으로는
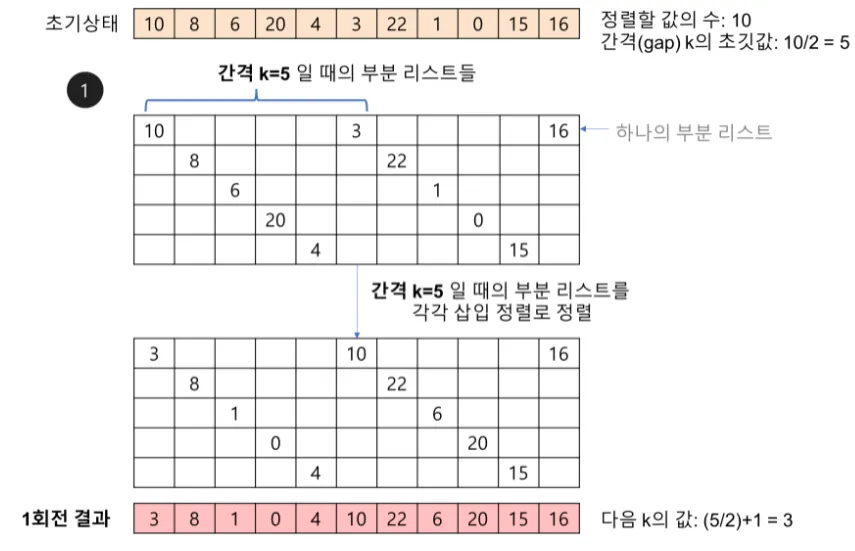
•
정렬해야 할 리스트의 각 k번째 요소를 추출해서 부분 리스트를 만든다. 이때, k를 ‘간격(gap)’ 이라고 한다.
•
간격의 초깃값: (정렬할 값의 수)/2 (정렬할 값의 수 / 3 + 1)로 하기도 한다
•
생성된 부분 리스트의 개수는 gap과 같다.
•
각 회전마다 간격 k를 절반으로 줄인다. 즉, 각 회전이 반복될 때마다 하나의 부분 리스트에 속한 값들의 개수는 증가한다.
•
간격은 홀수로 하는 것이 좋다.
•
간격을 절반으로 줄일 때 짝수가 나오면 +1을 해서 홀수로 만든다.
•
간격 k가 1이 될 때까지 반복한다.
구현
void shell_sort(char a[], int n)
{
int i, j, k, h, v;
for (h = n/2; h > 0; h /=2) {
for (i=0; i < h; i++) {
for (j = i+h; j < n; j += h) {
/* h간격에 있는 데이터 삽입 정렬 */
v = a[j];
k = j;
while (k > h-1 && a[k-h] > v) {
a[k] = a[k-h];
k -= h;
}
a[k] = v;
}
}
}
C
복사
void ShellSort(int A[ ], int n)
/* 입력: A[0:n-1] , n : 정렬할 원소의 개수.
출력: A[0:n-1] : 정렬된 배열. */
{ int h, i, j, Value;
h = 1;
do h = 3 * h + 1; while (h < n);
do {
h = h / 3; // gap 계산
for(i = h; i < n; i++) { // subfile 대해 삽입정렬
Value = A[i];
j = i;
while (A[j-h] > Value){
A[j] = A[j-h];
j -= h;
if (j <= h-1) break; // 교수님은 < 로 하셨는데 <=가 맞는 것 같습니다..
}
A[j] = Value;
} while ( h > 1);
}
C
복사
•
i, j, value 등 상수크기 메모리를 사용하므로 제자리성이 있습니다. 제자리 정렬
•
안정성은 X 불안정합니다. 거리가 떨어져 있는 데이터를 정렬하기 때문에 원래 순서와 다를 가능성이 큽니다.
•
시간복잡도 : 계산이 매우 복잡합니다
평균:
최악의 경우:
•
연속적이지 않은 부분 리스트에서 자료의 교환이 일어나면 더 큰 거리를 이동한다. 따라서 교환되는 요소들이 삽입 정렬보다는 최종 위치에 있을 가능성이 높아진다.
•
부분 리스트는 어느 정도 정렬이 된 상태이기 때문에 부분 리스트의 개수가 1이 되게 되면 셸 정렬은 기본적으로 삽입 정렬을 수행하는 것이지만 삽입 정렬보다 더욱 빠르게 수행된다.
알고리즘이 간단하여 프로그램으로 쉽게 구현할 수 있다.
퀵정렬
퀵 정렬은 찰스 앤터니 리처드 호어가 개발한 정렬 알고리즘이다. 다른 원소와의 비교만으로 정렬을 수행하는 비교 정렬에 속한다. 퀵 정렬은 n개의 데이터를 정렬할 때, 최악의 경우에는 O(n²)번의 비교를 수행하고, 평균적으로 O(n log n)번의 비교를 수행한다. 위키백과
•
분할 정복 알고리즘의 하나로, 평균적으로 매우 빠른 수행 속도를 자랑하는 정렬 방법
합병 정렬(merge sort)과 달리 퀵 정렬은 리스트를 비균등하게 분할한다.
•
분할 정복(divide and conquer) 방법
문제를 작은 2개의 문제로 분리하고 각각을 해결한 다음, 결과를 모아서 원래의 문제를 해결하는 전략이다.
분할 정복 방법은 대개 순환 호출을 이용하여 구현한다.
•
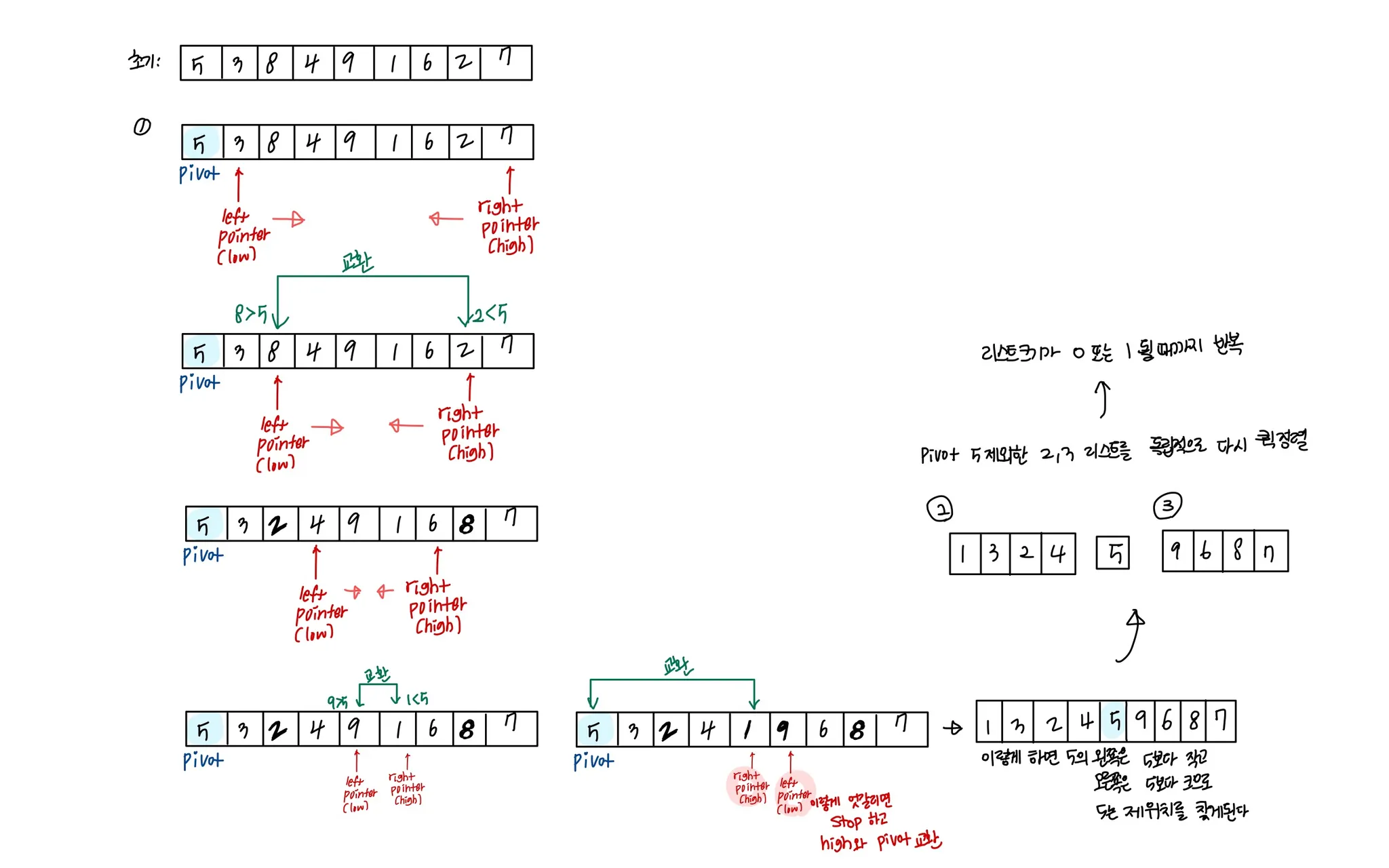
과정 설명
◦
리스트 안에 있는 한 요소를 선택한다. 이렇게 고른 원소를 피벗(pivot) 이라고 한다.
피벗을 기준으로 피벗보다 작은 요소들은 모두 피벗의 왼쪽으로 옮겨지고 피벗보다 큰 요소들은 모두 피벗의 오른쪽으로 옮겨진다.
(피벗을 중심으로 왼쪽: 피벗보다 작은 요소들, 오른쪽: 피벗보다 큰 요소들)
◦
피벗을 제외한 왼쪽 리스트와 오른쪽 리스트를 다시 정렬한다.
◦
분할된 부분 리스트에 대하여 순환 호출 을 이용하여 정렬을 반복한다.
◦
부분 리스트에서도 다시 피벗을 정하고 피벗을 기준으로 2개의 부분 리스트로 나누는 과정을 반복한다.
◦
부분 리스트들이 더 이상 분할이 불가능할 때까지 반복한다.
◦
리스트의 크기가 0이나 1이 될 때까지 반복한다.
(예시)
코드 구현
void swap(int* a, int* b)
{
int temp = *a;
*a = *b;
*b = temp;
}
int Partition(int A[], int Left, int Right)
{
// A[Left] : 분할 원소(분할 기준이 되는 원소)
int PartElem, Value;
PartElem = Left;
Value = A[PartElem];
do
do while(A[++Left] < Value);
do while(A[--Right] > value);
if (Left < Right) Swap(&A[Left], &A[Right]);
else break;
while(1);
A[PartElem] = A[Right];
A[Right] = Value;
return Right;
}
void QuickSort(int A[], int Left, int Right)
{
int k; // position of partition
if (Right > Left)
k = Partition(A[], Left, Right+1;)
QuickSort(A[], Left, k-1);
QuickSort(A[], k+1, Right);
}
C
복사
퀵 정렬은 다음의 단계들로 이루어진다.
1.
분할(Divide): 입력 배열을 피벗을 기준으로 비균등하게 2개의 부분 배열(피벗을 중심으로 왼쪽: 피벗보다 작은 요소들, 오른쪽: 피벗보다 큰 요소들)로 분할한다.
2.
정복(Conquer): 부분 배열을 정렬한다. 부분 배열의 크기가 충분히 작지 않으면 순환 호출 을 이용하여 다시 분할 정복 방법을 적용한다.
3.
결합(Combine): 정렬된 부분 배열들을 하나의 배열에 합병한다.
순환 호출이 한번 진행될 때마다 최소한 하나의 원소(피벗)는 최종적으로 위치가 정해지므로, 이 알고리즘은 반드시 끝난다는 것을 보장할 수 있다.
성능분석
제자리성 : 제자리 정렬 ( 그러나 순환함수의 임시 변수 및 복귀 주소 저장용 메모리가 추가 사용)
안정성 : 불안정 정렬
평균시간복잡도 :
최악시간복잡도 : → (예) 분할 원소가 항상 가장 큰 key이거나 가장 작은 key인 경우