오늘 연구실 세미나에서 VAE에 대한 내용을 다뤄서 간단히 정리해보았다.
Latent Space
예시를 한번 들어보겠다.
에서
: raw data point
: hidden or latent representation ()
: matrix for linear transform
: independent and identically distributed gaussian noise( 독립 항등 가우시안 분포 노이즈 )
로 생성되었다고 가정한다. 이 경우 raw data point인 는 로부터 linear transform을 통해 noisily generated되었다.
이는 PCA라는 고전적 방법의 가정과 일치하며, PCA는 를 찾는 과정이라 할 수 있다.
일반적으로 우리는 raw data 만을 보게되고 에는 접근하지 않는다. 이것이 를 hidden / latent representation이라 일컫는 이유이다.
그렇지만 우리는 더 근본적이고 압축된 데이터의 표현인 에 접근하면 좋을 것이다. ⇒ 어떠한 알고리즘에 사용할 유용한 input이 될 수 있다.
그러나 PCA는 가 의 선형변환인 경우만 가정하므로 실패하는 경우가 많다.
가 매우 복잡하고, 와 선형관계가 아닌 경우가 많기 때문이다.
그래서 사용하게 되는 것이 AutoEncoder이다.
AutoEncoder(AE)
VAE라는 말만 들으면 낯설게 느껴지지만 딥러닝을 공부해 본 사람이라면 autoencoder는 많이 들어본 단어일 것이다.
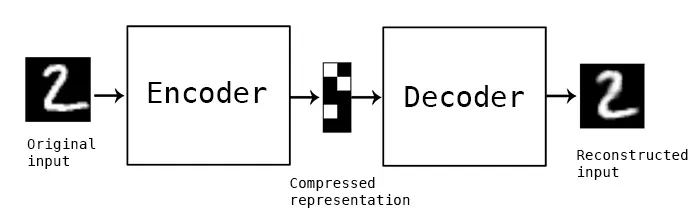
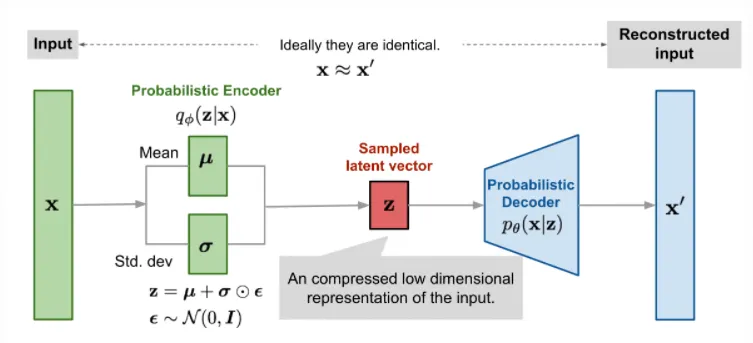
AutoEncoder란 원본 로부터 저차원의 representation 를 구해 스스로 네트워크를 학습하는 방법이다.
그림처럼 encoder와 decoder로 이뤄져있다. 가운데에 compressed representation이 이다.
•
encoder : 학습데이터를 latent variable vector로 잘 표현하는 역할
•
decoder : latent variable vector 로부터 학습데이터와 비슷한 데이터를 만드는 역할.
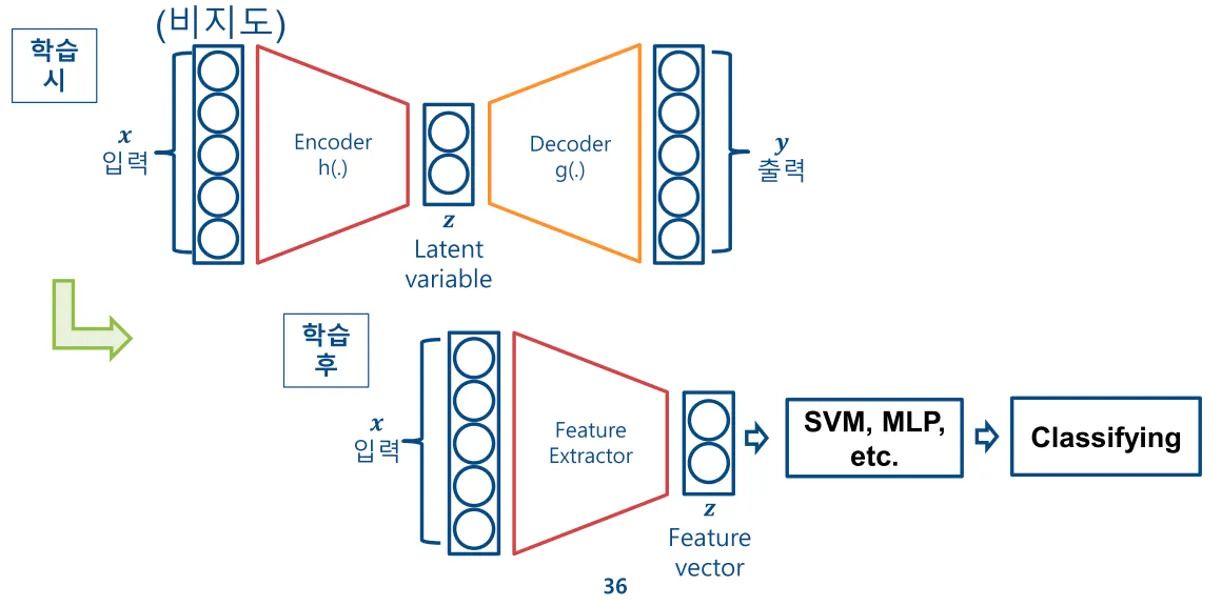
별도의 레이블이 없고, 원본데이터를 레이블로 사용하는 Unsupervised Learning이다.
주 목적은 encoder를 잘 학습해 성능 좋은 feature extractor로 사용하는 것이다.
입력 와 출력 가 최대한 동일한 값을 갖는 것이 목적이므로, loss는 입력값 와 decoder의 출력값 의 차이이다. ( e.g. L1 Loss, L2 Loss )
최소한의 성능을 보장할 수 있다는 점에서 장점이 있다 ( GAN같은 경우 최소한의 성능 보장 불가 )
Variational AutoEncoder(VAE)
AE와 유사한 구조를 가지지만 어떠한 의미에서 매우 다르다
VAE의 시작 → random noise로부터 원하는 영상을 얻을 수 없을까? (참고로 VAE는 GAN보다 훨씬 빨리 제안되었다)
단순히 생각해보면, 2D noise ( 크기)를 입력으로 얻을 수 있는 영상의 개수는 개이다. ( 픽셀값이 0~255니까 )
그 중 임의로 뽑은 랜덤노이즈로 내가 원하는 이미지를 얻을 수가 있을까? 말이 안된다.
그러나
라는 확률분포를 가지는 dataset을 사용해 이 dataset을 잘 나타내는 분포를 만들어 random noise가 그 분포 내에 속하도록하면 dataset과 유사한 결과값을 얻어낼 수 있을 것이다!
Uniform한 random noise가 아닌 dataset이 가지는 확률 분포 내에서 random noise를 생성
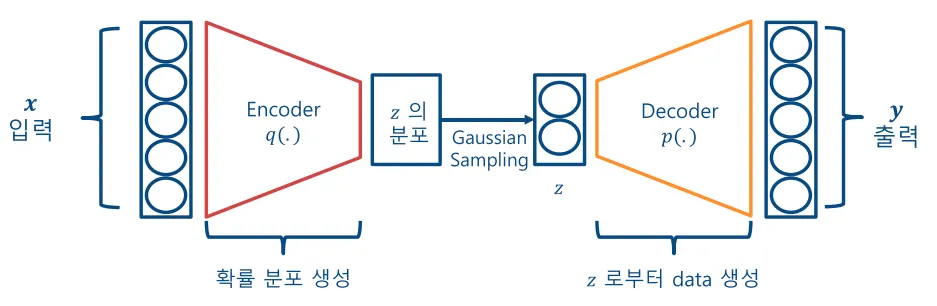
입력을 복원하는 AE와 달리 VAE는 데이터를 “생성”해야하기 때문에 데이터셋의 분포 그 자체를 학습해야 한다.
따라서 VAE는 위의 그림처럼 encoder에서 학습한 데이터의 분포 (의 분포)로부터 samping한 를 decoder의 입력으로 사용해 decoder는 로부터 데이터를 생성한다.
좀 더 detail하게 말하자면 z의 prior distribution을 으로 하고, 학습과정에서 평균 와 표준분포 를 학습한다.
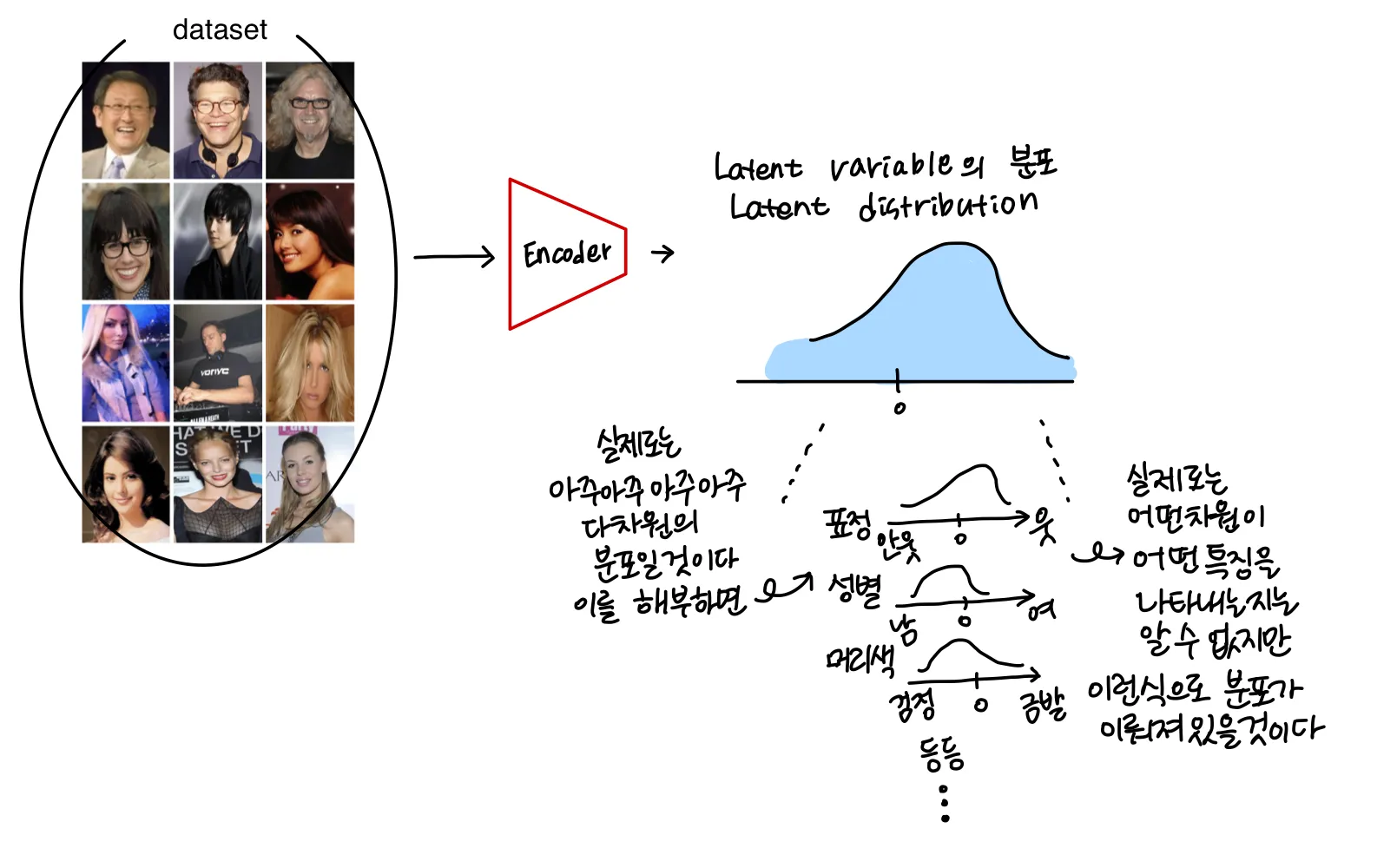
dataset이 encoder로 들어가면…
그림처럼 Latene distribution으로 나타내어진다. 실제 코드로 구현된 것에 따르면
위의 그림처럼 encoder로부터 와 가 추출되고, 을 따르는 ( prior distribution )으로 으로 를 sampling한다.
단순히 정규분포에서 sampling하는 형식으로 구현을 하면 encoder와 decoder 사이 latent variable 부분에서 backpropagation이 불가해지기 때문에 이렇게 와 값을 통한 선형 결합을 통해 gaussian 분포의 sampling을 하도록했다.
⇒ Reparameterization Trick
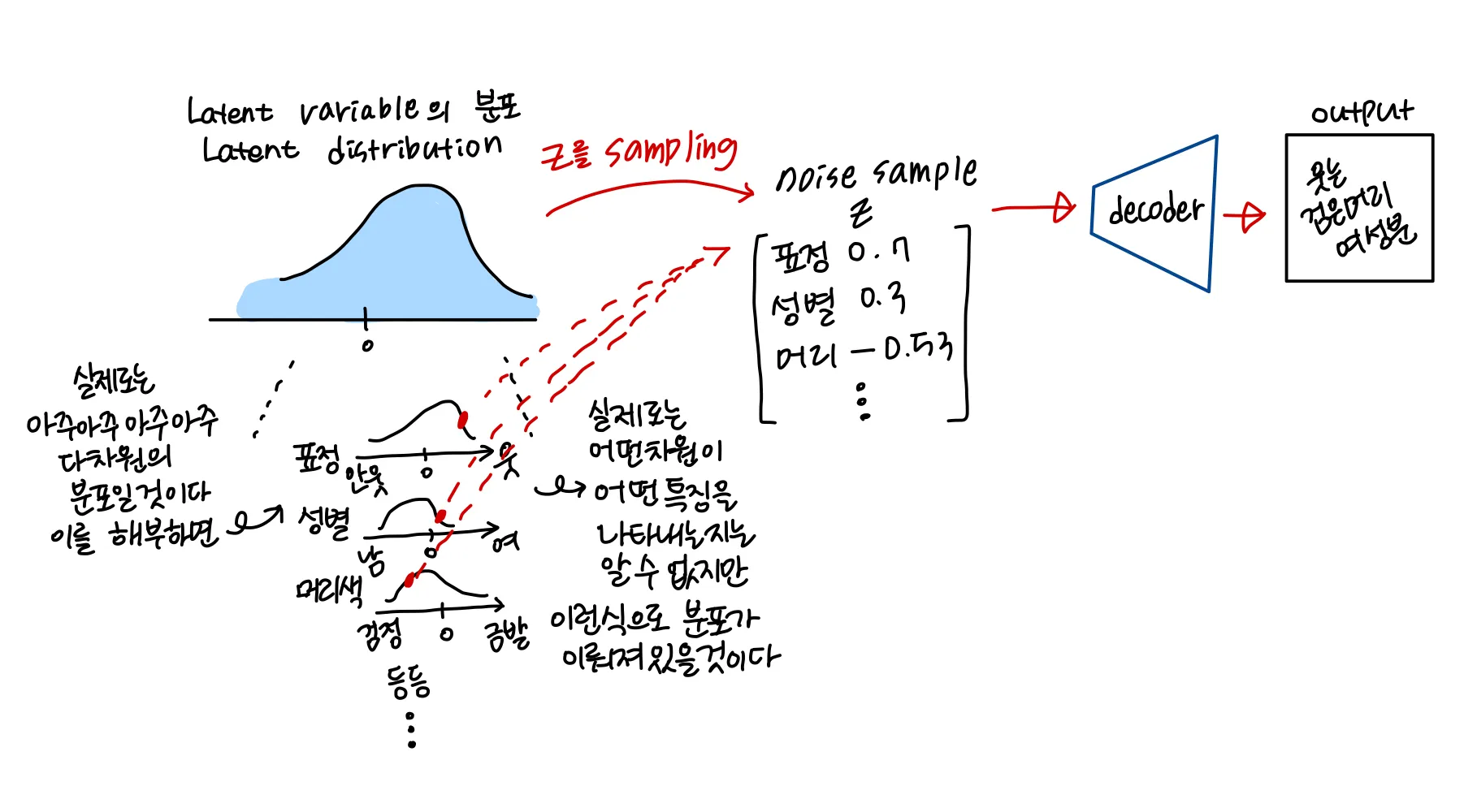
sampling된 가 decoder로 들어가면…
sampling된 는 매우 다차원의 Latent distribution에서 어떠한 특징에 대한 값을 갖고 있는 vector가 된다. sampling된 가 decoder로 들어가게되면 그림처럼 해당하는 feature에 대한 결과물이 output으로 나오게 된다.
당연히 sampling된 값에 따라 다르게 생긴 결과물이 나오게 될 것이다.
한마디로 정리하자면,
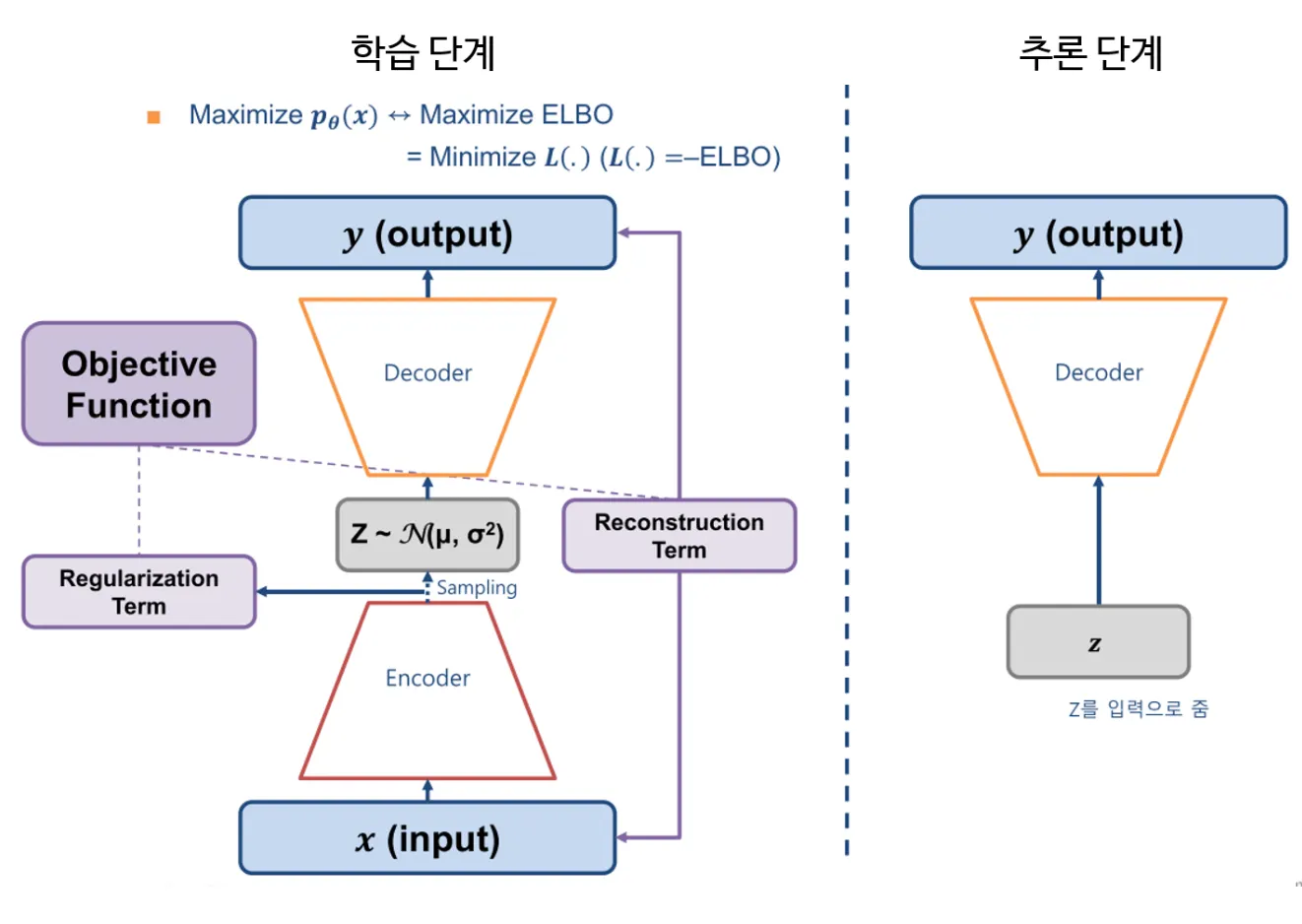
Training
•
encoder를 통해 Latent Distribution을 잘 예측하여 decoder에서 reconstruction이 잘 되도록 한다
Test
•
AutoEncoder에서와 같이 encoder 부분은 떼어내고 학습을 통해 정의된 Latent Distribution에서 latent variable z를 sampling해 decoder를 통해 새로운 이미지를 출력하도록 한다.
VAE의 단점
blurry output
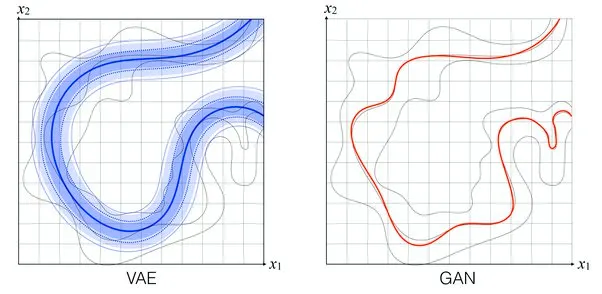
VAE에는 치명적인 단점이 있는데, sampling한 결과가 blurry한 특성이 있다는 것이다. 실제로 인터넷에는 GAN의 이미지가 왜 VAE보다 선명한것이냐! 라는 질문이 많이 올라와 있다. 아래 그림이 그를 잘 보여주는 이미지 이다.
위 이미지에서 회색으로 표시된 실선이 실제 이미지의 분포이다. 파란 부분이 VAE가 예측한 분포, 빨간 선이 GAN이 예측한 분포이다.
잘 생각해보자. VAE는 어떠한 분포 ( e.g. 가우시안 분포 )를 가정하고 시작하기 때문에 encoder가 예측한 분포는 그 분포를 따라야 한다. 가우시안 분포를 가정하고 시작했다면 encoder가 예측한 Latent distribution은 가우시안 분포여야 하는 것이다. 그렇기에 input image의 실제 분포를 정확히 따라가기 어렵다. 그림처럼 저 세개의 회색 선을 어우르면서도 가우시안 분포를 따르는 그런식으로 학습이 되는 것이다.→ blurry하면서 실제같지는 않은 결과물이 나옴.
반면에 GAN같은 경우에는 generator가 생성한 이미지를 discriminator가 실제 image와 구분하지 못할 때 학습이 끝난다. 이는 generator가 생성한 이미지가 실제와 똑같아야 끝나는 것이다! 그림을 보면 세가지 선중 하나의 선을 따라서 GAN이 학습되었다. 세가지 분포를 모두 담아내지는 못했지만 한가지 분포를 잘 모방했기에 어쩄든 Discriminator가 구분하지 못하게 된다. (이는 GAN의 고질적 문제인 mode collapse 문제를 나타내기도 한다. 데이터셋을 완전히 모방하지는 못했으나 하나의 mode만을 잘 모방해 discriminator를 속여버리는 문제 )
둘의 차이를 잘 나타낸 그림이었다.
Posterior collapse
또하나는 Posterior collapse문제이다.
이는 decoder가 encoder가 예측한 latent distribution 를 무시하고 결과를 내는 것을 말한다.
•
로부터 의 분포를 모델링하고, 그 분포로 부터 를 sampling할 때, sampling된 가 처음에 정의해준 prior distribution을 그대로 모방하는 현상 → 간단히 말해 가 의 정보를 제대로 담아내지 못하는 현상이다.
•
이 문제는 discrete한 데이터 (음성데이터라던지…) 에서 더 두드러진다고 실험적으로 밝혀졌다
◦
⇒ 이를 해결하기 위해 VQ-VAE라는 게 나왔는데, 추후에 또 다뤄보겠다!
reference