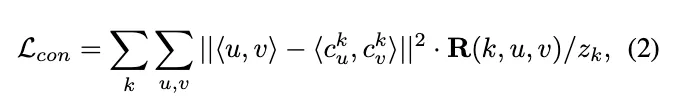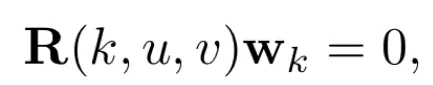Search
💗

SCOPS: Self-supervised Co-Part Segmentation (CVPR2019)

Co-Part segmentation 이라는 분야의 논문으로, 객체 내에서 part를 분류하여주는 연구이다.
이 논문에서는 parts가 객체에 대한 good intermediate representation으로 카메라, 포즈, 외형 변화에 robust하며, 이에 대한 기존 연구들은 supervised approaches가 대부분이 었다고 주장한다.
이는 매우 많은 수작업 annotations에 의존하며, unseen object categories에는 일반화되지 못하기 때문에 이 논문의 저자들은 self-supervised deep learning을 활용한 기법을 제안한다.
다양한 loss functions를 통해
•
기하학적으로(geometrically) 집중되어있고,
•
object variations에 대해 robust하며,
•
다른 object instances들 사이에 semantically consistent하도록 하였다

Introduction

기존 연구들의 단점

객체들을 분석하는 데에 주요한 장애물은 다양한 카메라 위치, 가려짐, 외형, 포즈 변화로 인한 object transformation, deformations에 대해 robust한 모델을 개발하는 것이다.
parts는 위 말한 것들에 대해 robust한 특징들을 제공해준다. 그로 인해 part segmentation은 3D reconstruction / detection / fine-grained recognition / pose estimation 등의 분야에서 사용되어왔다.
2D part represetnations로는 landmarks, bounding boxes, part segmentation이 주로 연구되어왔다.
part segmentation에 대한 가장 보통의 접근은 대량의 데이터로 fully supervised 로 접근하는 것이다.
그러나 annotation은 매우 비싸며 하나의 object category에 집중되어있기에 다른 클래스에 대해 일반화되지 못한다.
결과적으로 모델을 unseen categories까지 scale하기 위해서는 weakly supervised 기술들이 필요하다. (weak supervision or no supervision at all)

part representation의 필요성과 어려움

part representation은 한번 얻어지면 variations에 robust하고 높은 수준의 객체 이해를 돕는다.
그러나 intra-class variations 때문에 얻기가 매우 어렵다.
⇒ 하나의 객체 카테고리에 대한 하나의 image collection 은 같은 카테고리의 객체들임에도 불구하고 포즈나 외형, 카메라 뷰포인트, 여러 객체의 존재 등의 원인으로 매우 큰 다양성을 보인다. (같은 클래스 내의 다른 인스턴스들 간의 큰 차이)
이러한 다른 이미지들 사이의 관계성을 찾는 것이 weakly or unsupervised technique의 주된 과제가 될 것이다.
그래서 이 연구에서는 part segmentation에 대한 self-supervised deep learning framework인 SCOPS를 제안하며, 같은 카테고리 내의 하나의 이미지 컬렉션이 주어지면 모델은 다른 객체 인스턴스간에 semantically consistent한 part segmentation을 학습한다.
⇒ SCOPS는 class agnostic하다. 즉, class 는 분류하지 못 한다.
⇒ can be applied to any type of rigid or non-rigid object categories (???) rigid , non-rigid가 정확히 어떤 의미인지는 모르겠으나 카테고리에 제한 없이 모든 카테고리에 대해 수행이 가능하다는 말 같다.
저자들이 SCOPS를 설계하며 고려한 좋은 part segmentation의 조건들
1.
Geometric concentration : parts는 연결된 요소를 형성해야하고 geometrically 집중되어있어야 한다
2.
Robustness to variations : object deformations에 대해 robust해야 한다.
3.
Semantic consistency : 외형이나 포즈 변화가 있는 object instances간에 semantically consistent해야한다.
4.
Objects as union of part : parts는 objects(background가 아닌 영역) 위에 나타나야 하고 parts가 모여서 object를 구성해야 한다.
⇒ 이 조건들을 loss function에 담고자 하였다.

SCOPS의 장점

최근 (2019년도 기준) unsupervised landmark detection 방법들과 비교하였을 때
•
외형 변화에 더 robust 하고
•
occlusion을 더 잘 다루었다
•
고정된 수의 랜드마크를 찾는 landmark estimation과 달리 여러개의 object instances를 다룰 수 있다.
DFF(Deep Feature Factorization)과 비교하였을 때
•
더 큰 dataset으로 scale이 가능하고
•
object boundary에 잘 맞는 sharper part segments 생성이 가능하다.
•
object instances 간에 더 semantically consistent하다.

Related Work

Object concept discovery

Landmark detection

Dense image alignment

Image co-segmentation

SCOPS (proposed method)

같은 object category의 image collection이 주어지면, 하나의 이미지를 input으로 받고 part segmentation을 output하는 deep neural network를 학습하는 것을 목적으로 했다.
위에서 말한 특성들을 loss function에 담아 Gemetric concentration loss, Equivariance loss, Semantic Consistency loss를 설계했다.

Overall framework

Loss1. Geometric Concentration Loss

같은 객체를 이루는 part는 공간적으로 집중되어있고 연결된 요소를 구성한다. occlusion이 있거나 여러개의 instance가 있어도 마찬가지이다.
이 loss는 part response maps (R^\hat{\mathcal{R}}) 에 적용되어 part segments의 모양을 만든다.
모든 픽셀이 part center에 공간적으로 가깝게 만든다.
[part center cukc_u^k ]
⇒ 일종의 weighted average
[geometric concentration loss]
⇒ (zkz_k로 normalize한) 픽셀별 score와 center로부터의 L2거리의 곱의 합
⇒ 해당 part에 속할 score가 높은 픽셀일수록 part center와의 거리가 가깝도록 한다
⇒ 공간적 확률 분포인 R(k,u,v)/zk\bold{R}(k, u, v)/z_k 의 분산을 최소화하고자 한다.
이 loss는 unsupervised landmark estimation에서 landmark response map을 gaussian distribution에 가깝게 하고자 했던 Zhang et al.의 연구와 관련이 깊다.
이 연구에서는 이 loss를 part center에서 멀리 있는 part를 penalize하기 위한 목적으로 사용했다.

Loss 2. Equivariance Loss

이 loss는 part segmentation이 외형과 pose 변화에 robust하도록 하는 loss이다.
Spatial Transform + Color Jittering을 추가한 input의 part response map 인 R’R’과 원본의 part response map 인 RR 을 Spatial Transform한 결과의 KL-divergence distance 를 최소화하고,
⇒ part segmentation equivariance
R’R’의 center <cuk’,cvk’><c_u^{k’}, c_v^{k’}>와 spatial transformed center Ts(<cuk,cvk>)T_s(<c_u^k, c_v^k>)의 거리를 최소화한다.
⇒ part center equivariance
spatial transforms로는 random similarity transformations(scale, rotation, shifting)을 사용했다.
더 복잡한 것도 사용해보았지만 딱히 성능의 향상이 없었다고 한다.
center에 대한 부분은 landmark estimation에서 사용이 되었었으나 part segmentation에 대해 확장시켰다고 한다.

Loss 3. Semantic Consistency Loss

Equivariance loss에서 합성으로 만들어진 변환은 다른 instance 간의 consistency를 생성하기에 부족할 수 있다. 현실의 외형적인 차이는 인공적인 변형으로 만들어내기에 너무 크기 때문이다.
semantic consistency를 위해서는 다른 Instances들을 loss에 녹여야 한다.
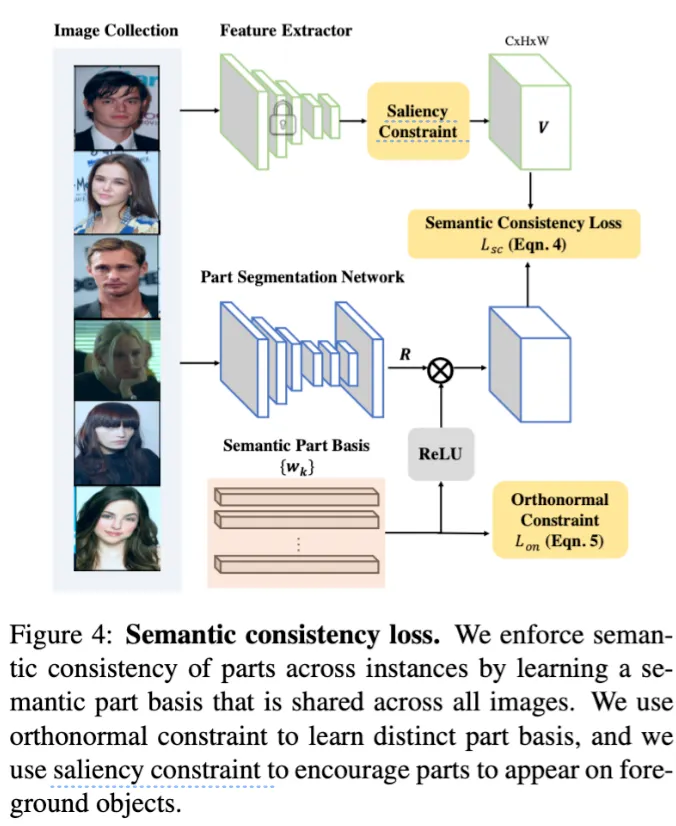
key : 객체와 파트들에 대한 정보는 classification network의 CNN features에 임베딩되어 있다.
저자들은 주어진 classification features에서 각각의 part들과 관련있는 representative feature clusters를 찾을 수 있을 것이라고 생각했다.
spanning, subspace, basis등 선형대수 용어로 가득하지만 심플하게 (u,v)(u, v) 위치에 대해서 part segmentation response의 각 part에 대한 weight를 이용해 ww들을 weighted sum 해서 그것이 V\bold{V}와 유사하게 하는 것이다. 그렇게 하면 위에서 설명한 것 처럼, (u,v)(u, v)가 k part에 속할 가능성이 높다면 wk\bold{w}_k와 유사하게 된다.
R\bold{R}과 {wk}\{\bold{w}_k\}는 backpropagation으로 동시에 학습된다.
basis vectors가 서로를 가감시키지 않도록 ReLU를 통해 V\bold{V}와 basis vectors에 ReLU로 non-negativity를 강제했다. (R\bold{R}은 softmax로 인해 이미 non-negative이다.)
⇒ semantic consistency loss를 linear subspace recovery problem으로 정의
(여기서 subspace는 image collection에 대한 feature extractor가 제공하는 embedding space)
학습과정에서 part bases (wk\bold{w}_k들)는 점진적으로 imagenet pretrained deep features가 제공하는 embedding space 내에서 각 part를 가장 잘 나타내는 방향으로 수렴할 것이다.
그리고 recovered subspace (∑kR(k,u,v)wk\sum_k\bold{R}(k, u, v)\bold{w}_k)는 span of the basis {wk}\{\bold{w}_k\}라고 할 수 있다.
⇒ 같은 part의 response는 pre-trained feature space에서 비슷한 semantic feature embedding을 갖도록 학습되게 때문에 instance간의 semantic consistency를 강제하게 된다.
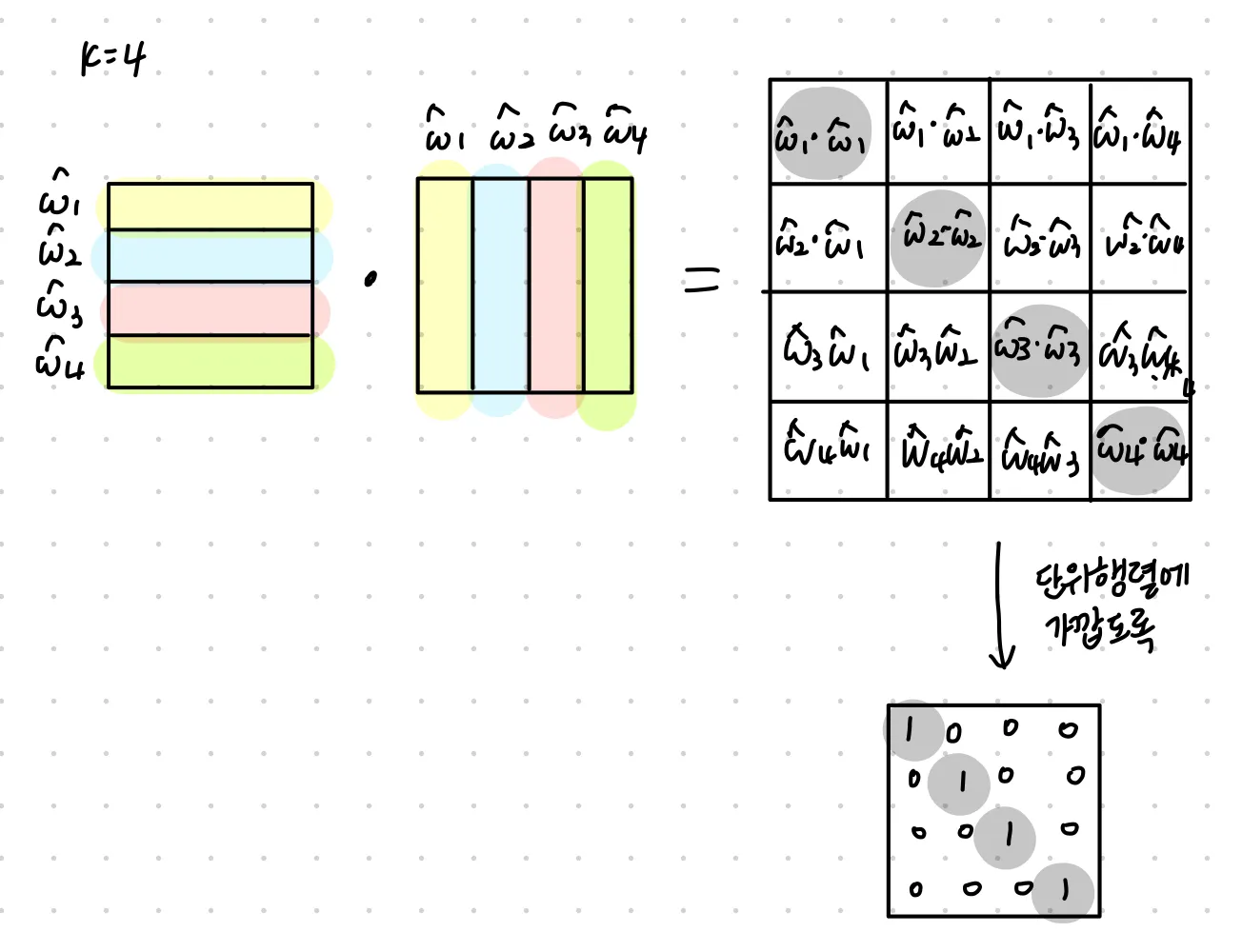
Orthogonal constraint
semantic consistency loss를 학습 할 때 다른 basis임에도 비슷할 수 있다 (특히 K가 매우 크거나 subspace의 underlying rank가 K보다 작을 때)
basis끼리 비슷하면 part segmentation이 noisy해질 수 있다. 그래서 orthogonal constraint를 통해 이를 방지한다. 말 그대로 wk\bold{w}_k 끼리 orthogonal하도록 하는 것이다. (주성분 분석에서의 컨셉과 유사해보인다)
W^\hat{\bold{W}} : 각 row가 normalized part basis vector w^k=w^k/∣∣w^k∣∣ \hat{\bold{w}}_k= \hat{\bold{w}}_k/|| \hat{\bold{w}}_k|| 인 matrix
orthogonal constraint on loss function on W:
∣∣∙∣∣F2|| \bullet ||_F^2 는 Frobenius norm(vector의 L2norm을 행렬로 확장)이며 IK\mathbb{I}_K 는 KxK의 단위행렬(identity matrix)이다.
이를 그림으로 나타내면 다음과 같다
즉, 다른 basis vector와의 dot 연산 결과가 0에 가깝도록 한다 == 다른 basis vector와의 각도가 90도에 가깝도록 한다. ⇒ basis vector간의 연관성을 최고화하고 basic set을 더 정확히 해 더 나은 part response를 얻는다
Saliency Constraint
image collection이 작거나 part 수 K가 너무 크면 일반적인 background를 object parts로 잘못 잡아내는 경우가 있었다고 한다. 그래서 이를 해결하기 위해 unsupervised saliency detection method 를 사용해 V\bold{V} 내의 BG features를 suppress한다. 그로 인해 part basis가 background regions에 관련되지 않을 수 있다.
unsupervised saliency map D∈[0,1]H×W\bold{D} \in [0,1]^{H \times W}
D∘V\bold{D} \circ \bold{V} 로 feature map V\bold{V}를 soft-mask 한다. (hadamard product)
D(u,v)=0\bold{D}(u,v) = 0 인 픽셀들(non-salient pixels)에 대해 semantic consistency loss는 다음과 같이 변형되어 BG 영역을 null space로 projecting해 R(k,u,v)wk\bold{R}(k,u,v)\bold{w}_k 를 0이 되도록하는 것이 된다.
이 saliency constraint 는 이 논문의 prior knowledge인 part는 객체 위에서 나타나야하며 파트들이 모여서 객체를 이루어야 한다는 것을 담고 있다.
semantic constraint와 관련해 DFF라는 기존 연구는 w들을 선형결합하지 않고 V\bold{V}를 바로 RW\bold{RW}에 가깝도록 한다.
DFF 와 이 연구의 다른 점은
1.
mini-batch와 일반 gradient descent를 사용할 수 있다.
•
DFF는 inference 시 전체 image collection이 필요하다
2.
part segmentation과 basis를 neural network로 학습함으로써 다른 제한들 (orthogonal constraint같은 것)을 적용하기가 쉽다.

Experiments

•
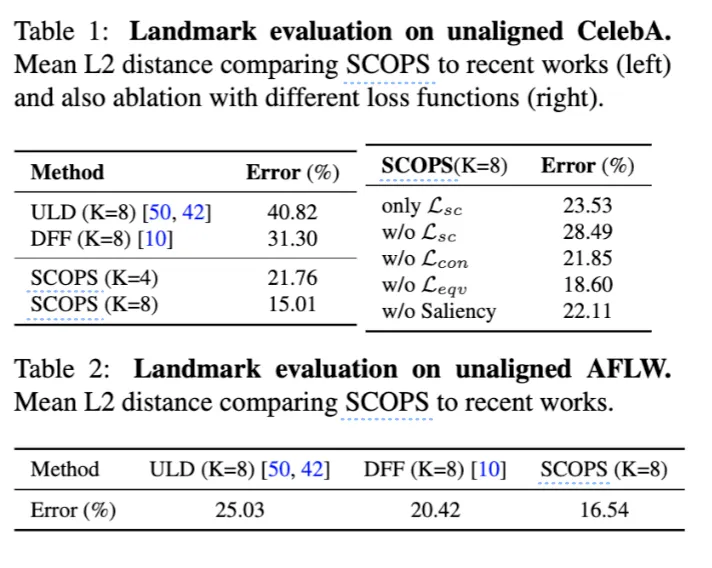
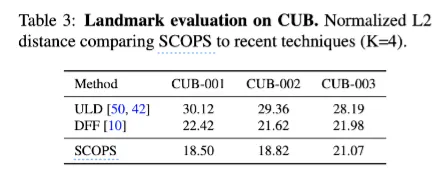
CelebA와 AFLW, CUB에 대해서는 part segmentation을 landmark로 바꿔서 GT annotations와 비교했다. ( part segmentation 결과 뒤에 linear regressor 추가해 바꿈 )
•
PASCAL VOC에 대해서는 part segmentation 결과를 합쳐서 foreground segmentation IOU를 쟀다.
Made with