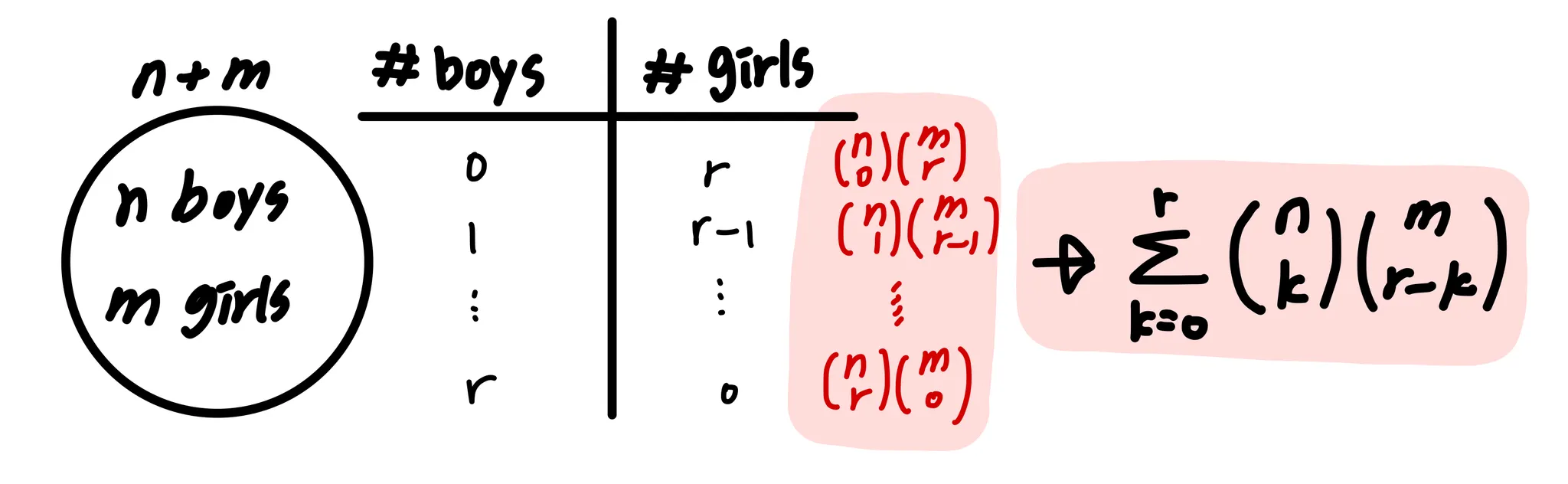Search

[작성중]독립사건과 확률 (+ 순열 및 조합)

※ KOCW 이상화교수님의 확률 및 통계 강좌를 기반으로 정리한 내용입니다
독립과 조건부 확률 ⇒ 이전 글 참고

Combinational Analysis

1. Permutation (순열)

서로 다른 n개 중 r개의 요소를 일렬로 나열(line arrangement)하는 방법 ⇒ 순서 O
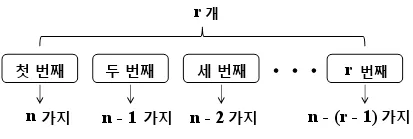
순열의 경우의 수는 다음과 같이 계산한다.
•
아직 아무것도 나열하지 않았기에 첫번째 자리에는 n개를 놓을 수 있다
•
두번째에는 하나를 나열한 상태이기에 n-1개를 놓을 수 있다
•
이를 반복하면 r번째에는 n-(r-1)개를 놓을 수 있다.
•
이를 식으로 정리하면 n개 요소중 r개를 나열하는 경우의 수는 n(n-1)(n-2)…(n-(r-1)) 가지이다.
•
이는 기호로 다음과 같이 표현할 수 있다.
nPr=n!(n−r)!_nP_r = \frac{n!}{(n-r)!}

Group permutation

요소간에 중복이 있는 경우의 순열이라고 할 수 있다.
ex )
10개의 공이 있는데 빨간공이 5개, 하얀공이 3개, 파란공이 2개이다. (10 = 5 + 3 + 2)
이것을 어떻게 나열할까?
(빨간공에 숫자가 붙어있다고 가정하면) 빨간공 1 빨간공 2 빨간공 3을 놓던 빨간공 2 빨간공 3 빨간공 1을 놓던 (색으로 봤을 때) 같은 경우의 수이다.
그러면 중복되는 경우의 수를 나누어주어야 할 것이다. 여기서는 다음과 같이 연산 될 것이다.
10!5!3!2!\frac{10!}{5!3!2!}
식으로 정리하면 다음과 같다.
n!n1!n2!...nk!\frac{n!}{n_1!n_2!...n_k!}

Circular Permutation(순환수열)

고정 원 주위에 n개의 개별 개체를 배열할 수 있는 총 방법 수
이 경우는 두가지로 나눌 수 있다.
•
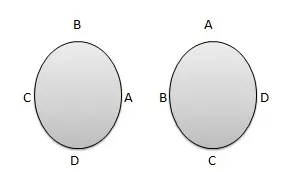
case 1 : 시계방향 순서와 반시계방향 순서를 다르게 보는 경우
•
case 2: 시계방향 순서와 반시계방향 순서를 같게 보는 경우
위 그림은 case1의 경우 다른 경우의 수로 취급되고 case 2의 경우 같은 경우의 수로 취급된다.
수식은 다음과 같다
•
case 1 :Pn=(n−1)! P_n = (n-1)!
⇒ n!/nn! / n ⇒ n개 일단 나열한 후 회전 n칸 가능하므로 n으로 나눠줌
•
case 2 : Pn=(n−1)!2!P_n = \frac{(n-1)!}{2!}
⇒ 시계방향과 반시계방향이 하나의 경우로 취급되므로 case 1에서 2로 나눠줌 (2번중복으로 봄)

2. Combination (조합)

n개 중 r개를 뽑기(select) ⇒ 순서 X
수식은 다음과 같다.
nCr=nPrr!=(nr)=n!(n−r)!r!_nC_r=\frac{_nP_r}{r!} = \begin{pmatrix} n\\r\end{pmatrix}=\frac{n!}{(n-r)!r!}
•
n개 중 r개 나열하는 순열을 계산하고, r개 안에서 어떻게 배열되든 같은 경우의 수이기에 r!로 나누어준다.
•
group permutation 취급하되 n개 나열한 후 뽑히는 것과 안 뽑히는 것을 각각 중복으로 보고 나눠준다.
이러한 경우에는 어떨까
(n+mr)\begin{pmatrix} n+m\\r\end{pmatrix} ⇒ n+m개에서 r개를 뽑는 경우
예시를 들어 해석해본다.
ex ) 남학생 n명 여학생 m명 중 r명을 뽑는 경우
이 공식은 이후 이항분포와 2개 이상의 변수를 다룰 때 사용된다.

Binomial Thorem (이항정리)

이항정리의 공식은 다음과 같다
(a+b)n=A0an+A1an−1b+...+Anbn=∑k=0n(nk)akbn−k=∑k=0n(nk)an−kbn(a+b)^n = A_0a^n + A_1a^{n-1}b + ... + A_nb^n \\= \sum_{k=0}^n \begin{pmatrix} n\\k\end{pmatrix}a^kb^{n-k} = \sum_{k=0}^n \begin{pmatrix} n\\k\end{pmatrix}a^{n-k}b^{n}
이 식에서 a=1, b=x를 대입한 버금 공식 (딸림 공식)은 중요한 의미가 있다.
f(x)=(1+x)n=∑k=0n(nk)xkf(x) = (1+x)^n = \sum_{k=0}^n \begin{pmatrix} n \\ k\end{pmatrix} x^k
x=1x = 1일 때: 2n=∑k=0n(nk)2^n = \sum_{k=0}^n \begin{pmatrix} n \\ k \end{pmatrix} : n에 대한 모든 가능한 조합의 합
x=−1x = -1일 때: 0=∑k=0n(nk)(−1)k0 = \sum_{k=0}^n \begin{pmatrix} n \\ k \end{pmatrix}(-1)^k : 짝수 번째 항이 더해지고 홀수 번째 항이 빼진다
→ 위 두개를 더하게 되면 k가 짝수인 항만 남게된다. : nC2+nC4+..._nC_2 + _nC_4 + ...
→ x=1x=1일 때에서 x=−1x=-1일 때를 빼면 k가 홀수인 항만 남게된다 : nC1+nC3+..._nC_1 + _nC_3 + ...
⇒ 홀수번째만 남던 짝수번째만 남던 어쨌든 절반만 남는 것이기 때문에 둘 다 2n−12^{n-1} 의 값을 갖게 된다.
미분을 하면?
f′(x)=n(1+x)n−1=∑k=0nk(nk)xk−1f^{\prime}(x) = n(1+x)^{n-1} = \sum_{k=0}^nk \begin{pmatrix}n\\k\end{pmatrix}x^{k-1}
x=1x = 1일 때 f′(1)=n2n−1=∑k=0nk(nk)=nC1+2nC2+3nC3+...f^{\prime}(1) = n2^{n-1}= \sum_{k=0}^nk\begin{pmatrix}n\\k\end{pmatrix}=_nC_1+2_nC_2+3_nC_3 + ...
f′′(x)=n(n−1)(1+x)n−2=∑k=0nk(k−1)(nk)xk−2f^{\prime\prime}(x) = n(n-1)(1+x)^{n-2} = \sum_{k=0}^nk(k-1) \begin{pmatrix}n\\k\end{pmatrix}x^{k-2}
x=1x = 1일 때 f′′(1)=n(n−1)2n−2=∑k=0nk(k−1)(nk)=nC2+3×2nC3+...f^{\prime\prime}(1) = n(n-1)2^{n-2}= \sum_{k=0}^nk(k-1)\begin{pmatrix}n\\k\end{pmatrix}=_nC_2+3\times2_nC_3 + ...

이러한 것들이 왜 필요할까?

이항분포의 확률이 이를 통해 유도되기 때문!
이항분포 (Binomial Distribution) : 연속된 n번의 독립적 시행에서 각 시행이 확률 p를 가질 때의 이산확률분포.
확률 변수 kk가 매개변수 nn과 pp를 가지는 이항분포를 따른다면 k∼B(n,p)k \sim B(n, p)라고 표한하며 nn번 시행 중 kk 번 성공할 확률은 다음과 같은 확률 질량 함수로 주어진다.
BP(n,p)=(nk)pk(1−p)n−kBP(n, p)=\begin{pmatrix}n\\k\end{pmatrix}p^k(1-p)^{n-k}
•
평균 m=npm = np, 분산 σ2=np(1−p)\sigma^2= np(1-p)

조합을 통해 복잡한 합을 간단하게 구하기

ex 1.
∣x∣<1|x| < 1일 때
f(x)=1+2x+3x2+4x3+…f(x) = 1 + 2x + 3x^2 + 4x^3 + …
xf(x)=x+2x2+3x3+…xf(x) = x + 2x^2 + 3x^3 + …
f(x)−xf(x)=(1−x)f(x)=1+x+x2+x3+…=11−xf(x) - xf(x) = (1-x)f(x) = 1+ x + x^2 + x^3 + … = \frac{1}{1-x}
ex 2.
g(x)=∑k=0∞xk=11−xg(x) = \sum_{k=0}^\infin x^k=\frac{1}{1-x}
g′(x)=∑k=0∞kxk=f(x)g^{\prime}(x) = \sum_{k=0}^\infin kx^k=f(x)
⇒ 이런 모양의 f(x)f(x)가 구하고싶다면, g(x)g(x)를 미분하는 방식으로 구할 수 있다. ⇒ (11−x)′(\frac{1}{1-x})^{\prime}
등차수열과 등비수열의 곱으로 이뤄진 멱급수의 합을 구할 때 위와 같은 방식으로 유도해서 구할 수 있다.

Stirling formula ( Stirling’s approximation)

큰 계승을 구하는 근사법
n!에서 n이 매우 커지면 구하기 정말 어렵다. 이를 근사시키는 rule이다.
n!∼2πn(ne)nn! \sim \sqrt{2\pi n}(\frac{n}{e})^n
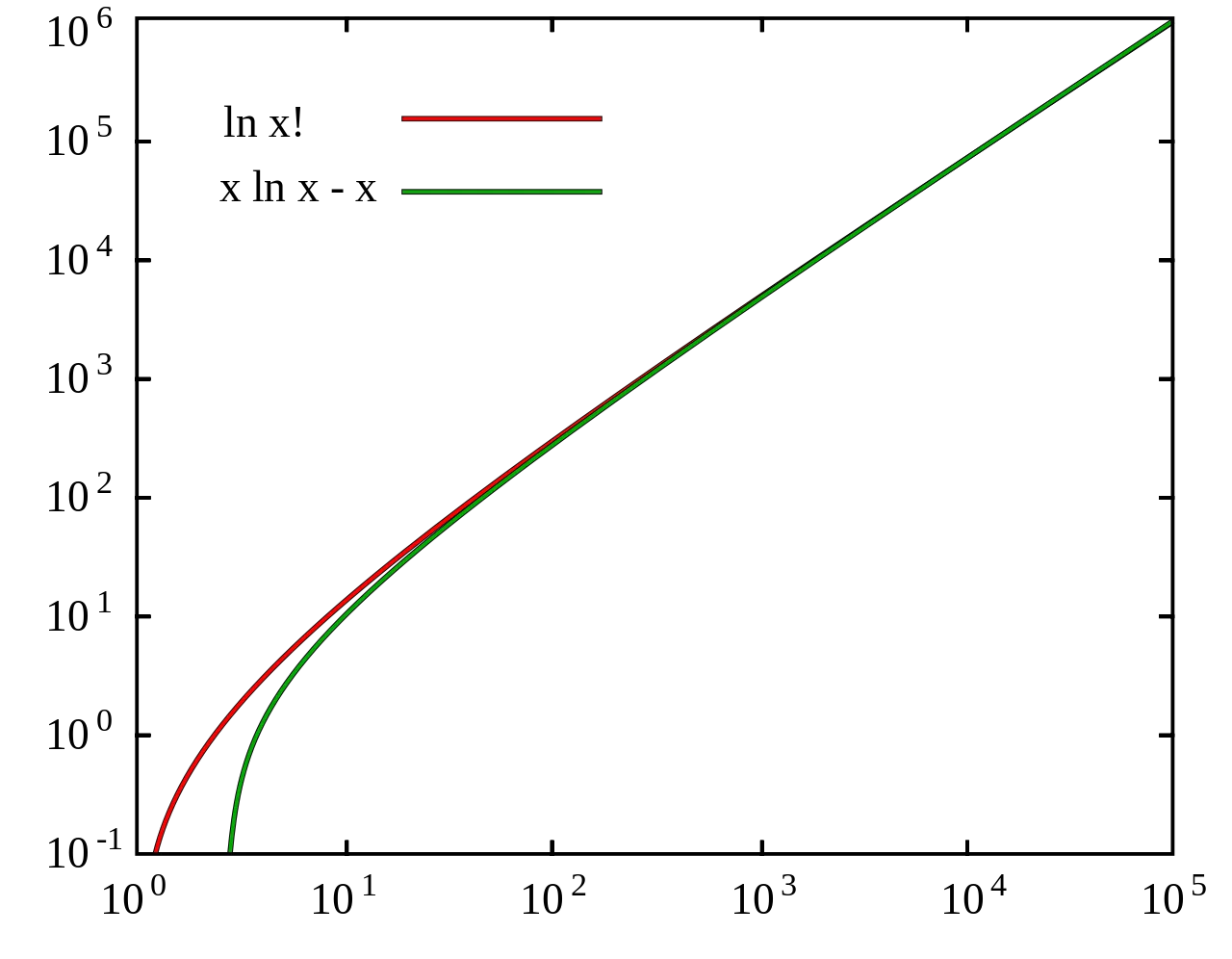
그래프를 보면 알 수 있듯, n값이 커질 수록 점점 근사의 오차가 줄어든다.
충분히 큰 n에 대하여 유효한 근사가 된다.

Reliability

46:19
어떤 시스템이 어떤 시간동안 얼마나 고장나지 않고 잘 동작하는지
time 입장에서의 duration을 의미한다.
Made with