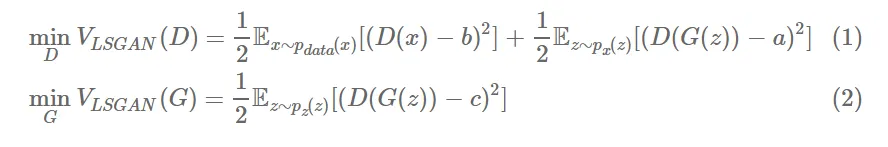DCGAN / cGAN등의 기존 모델들 → Binary Crossentropy로 min-max game문제 해결
위의 글을 보면 직관적으로 이해할 수 있다.
BCE Loss를 objective function으로 사용하게되면 Vanishinh gradient 문제가 발생한다
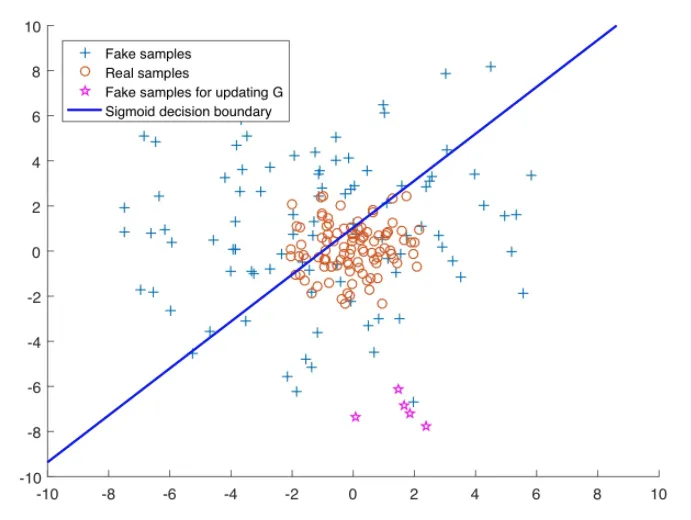
논문은 이러한 이미지로 그 이유를 설명한다
sigmoid decision boundary 위의 데이터들은 fake로, 아래 있는 데이터들은 real로 판단한다.
real data인 o 들이 가운데에 모여있고, GAN의 목표는 + 인 fake sample들을 o들의 분포에 가깝게 만드는 것이다.
☆ 이 G를 업데이트하기위한 fake데이터들인데, fake임에도 이미 real로 분류가 되어있기에 D를 속이는 임무를 완료한 것으로 간주된다. 즉, G 업데이트에 도움을 주지 않는다 ( Real 데이터의 분포에서 멀리 떨어져있는데도 불구하고 말이다 )
이 문제를 vanishing gradient 문제로 정의한다.
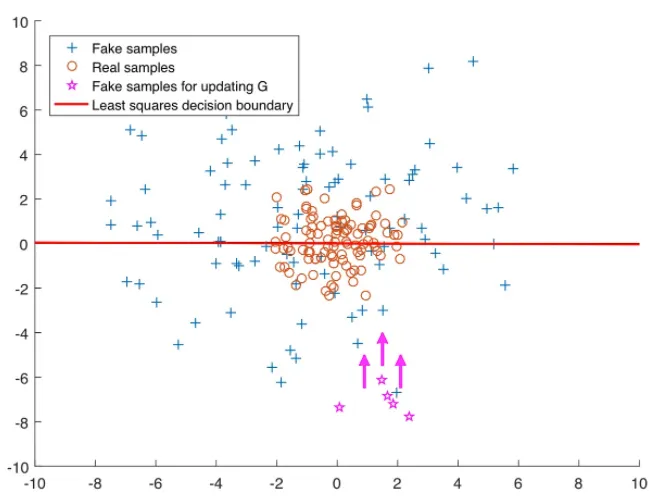
그래서 저 ☆ 데이터들을 real data쪽으로 끌어오자! 라는 것이 LSGAN의 목표입니다
이를 위해 BCE Loss 대신에 decision boundary 에서 멀리 떨어진 samples에게 페널티를 부여할 수 있는 Least Square Loss를 사용하자고 제안합니다
Least Square Loss를 한마디로 설명하면, 가짜 데이터와 실제 값의 차이를 측정해 제곱 ( 음수인 경우 처리를 위해 ) 해서 그 거리를 낮추는 방향으로 학습을 진행하는 것이다.
위의 그래프를 보면, 빨간색 Least Squares Decision Boundary에서 멀수록, Least Square 를 사용하기 때문에 페널티를 주게된다 ( boundary가 왜 저런지는... 이해하기보다는 설명하기 위해 간단히 표현한 그림으로 생각해야할 것 같다 )
⇒ 좀 더 real한 데이터 분포에 가깝게 위치시킬 수 있음!
식은 이렇다
•
a : fake label
•
b : real label
•
c : the value that G wants D to believe for fake data → 코드에선 real label 로 넣어서 학습합니다
D의 Loss
•
D(x) , 즉 real data의 판별값과 real label간의 차이를 최소화하는 방향으로 학습
•
D(G(z)), 즉 fake data의 판별값과 fake label 간의 차이를 최소화하는 방향으로 학습
G의 Loss
•
D(G(z)), 즉 fake data의 판별값과 속이고자하는 라벨값과의 차이를 최소화하는 방향으로 학습