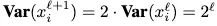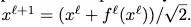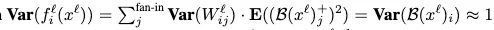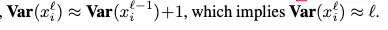Prior Knowledge
Normalization이란?
normalization이란 간단히 말하면 데이터 혹은 피쳐의 값의 범위를 일정 범위로 제한해주는 것이다.
0~1사이 값이 될 수도 있고, 어떠한 분포 ( e.g. 표준정규분포 ) 일수도 있다.
ex) logistic regression에서 input data를 표준정규분포(평균이 0, 분산이 1) 로 normalization하기
Batch Normalization
Batch Normalization Biases Residual Blocks Towards the Identity Function in Deep Networks(Camera-ready version of NeurIPS 2020)
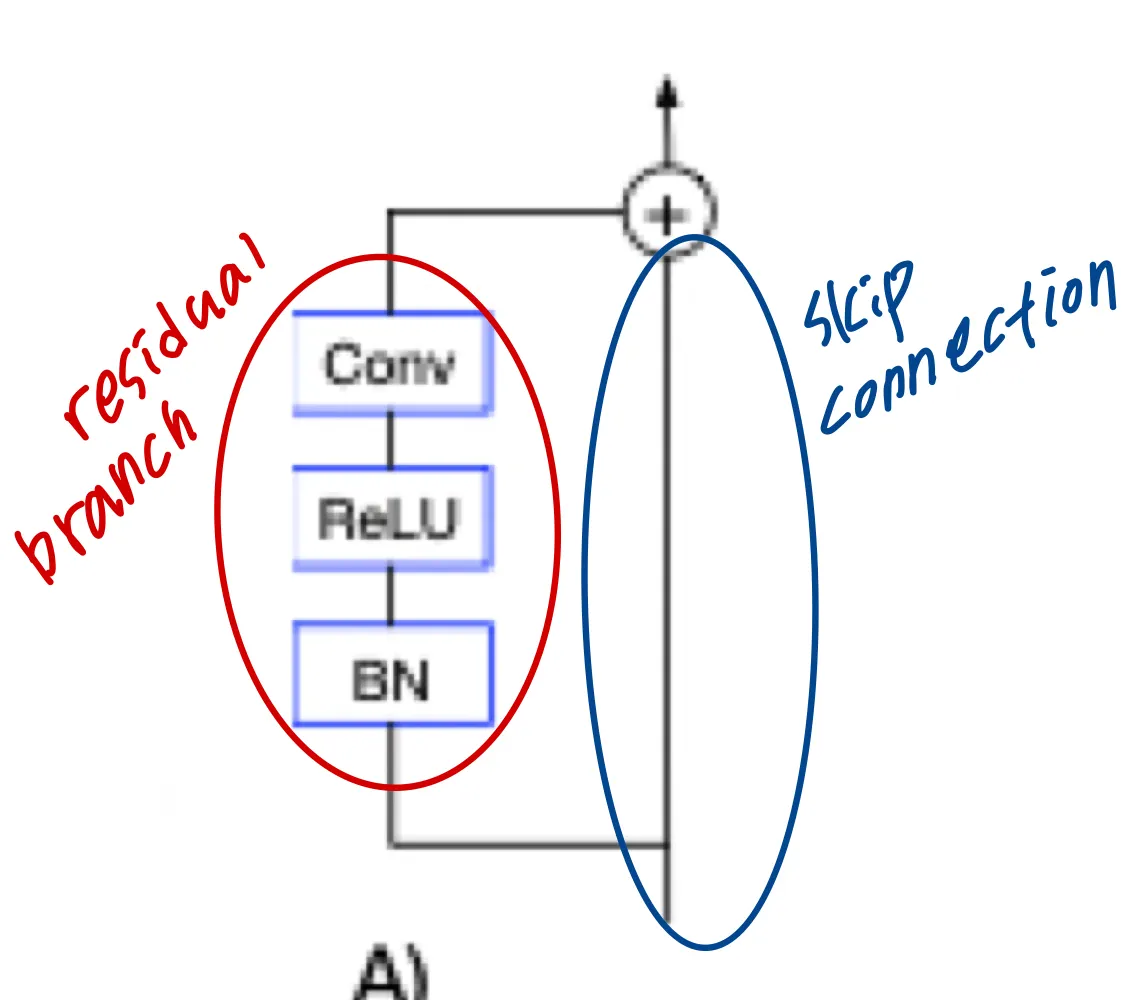
BN이 residual network의 학습 가능한 depth를 크게 증가시켰지만, 이는 학습 초반 BN이 skip connection에 대해 residual branch를 downscale하기 때문에 발생하는 것이라고 주장하며, 이를 실험으로 증명하는 논문입니다. 이는 결국 BN이 적용된 residual blocks의 연산이 거의 identity function()에 가깝고, 이 사실을 기반으로 BN없이 deep residual network를 학습시킬 수 있는 Skipinit 방식을 제안합니다.
Introduction
skip connection + batch normalization ⇒ 학습 가능한 nerual network 의 depth를 크게 증가시켰지만 BN의 효과의 기원이 잘 이해되지 않아왔다.
그럼에도 layer noramlization과 transformer 구조가 소개됨에 따라 대부분의 SOTA모델이 skip connection + normalization 조합을 사용하고 있다.
contributions
•
왜 BN이 deep residual network를 쉽게 학습시키는지 설명한다
◦
BN이 hidden activations를 차수로 downscale한다는 것을 증명 ( 학습 초기에 )
◦
depth가 깊어질수록 residual blocks는 점점 skip connection에 지배되게 되고 residual blocks에 의해 연산되는 함수들은 identity에 가깝게 된다. 그래서 signal propagation을 보존하고 well-behaved gradients를 보장해준다.
•
위의 주장이 맞다면 normalization 없어도 residual branch만 downscale해준다면 deep residual network의 학습이 가능할 것이다.
◦
그래서 Skipinit이라는 방식을 소개한다. 1000개의 레이어를 갖는 deep residual network를 학습가능하게 하는 normalization을 대체하는 방식이다.
•
batch size의 범위에 따라 residual network에 대한 경험적 연구를 제공한다
◦
BN이 residual network를 큰 learning rate로 학습할 수 있게 하지만, 이는 batch size가 클 때만 적용된다는 사실을 증명한다
◦
batch size가 작으면 normalize를 사용하건 안하건 최적의 lr은 비슷하다. 그러나 normalized networks가 더 높은 test accuracies와 더 낮은 training losses를 달성하긴 한다.
◦
이 실험은 residual network에서, 가장 큰 안정적인 lr이 BN의 주된 benefit이 아니라는 것을 증명한다(이전의 연구들을 반대)
Why are deep normalized residual networks trainable?
•
normalized residual network가 non-residual 인 모델들보다 2배정도 더 깊은 network를 학습할 수 있다.
이 효과 이해 위해 학습 초반 single training example의 hidden activations를 분석하였다.
<실험 조건>
: 번째 residual block의 번째 요소
: model 의 input이며 각 독립적인 component 에 대해 평균이 0, 분산이 1
: 번째 residual block의 residual branch
으로 ReLU의 output
: batch normalization 연산
single linear layer
1.
unnormalized :
2.
normalized :
는 HE initialization 적용 ( linear layer )
따라서 ⇒ residual branch의 output의 번째 coordinate의 평균
이기 때문에, 모든 에 대해
residual branch 와 skip connection의 covariance 이다. 왜냐하면 hidden activation의 variance때문이다 :
covariance (공분산)이 0이라는 것은 두 확률변수가 독립이라는 의미이다.
<논문의 실험의 결론>
unnormalized networks : 여기서는 BN이 없으면 residual block이 identity function이 아니라는 것을 증명합니다.
residual branch의 variance == skip connection 의 variance
이 사실이 암시하는 것은
1.
hidden activations의 variance가 depth에 지수적으로 폭증한다.
⇒ 해결방법
residual block의 output을 로 나눠준다.
2.
이기 때문에, residual branch와 skip connection은 residual block에 똑같이 기여한다. == residual block이 identity function이 아니다.
normalized networks : 여기서는 학습초반 residual block이 identity function에 가까움을 증명한다.
reidual branch의 variance가 1이고
번째 residual branch의 input의 variance가 이다.
•
hidden activations의 분산의 증가는 beneficial 하다
◦
이면 BN은 l번째 residual branch의 분산을 l의 factor로 억제해야되기 때문이다. ( batch normalization 식을 보면 이해가 간다 )
◦
따라서 residual branch는 residual block output의 분산의 만큼만 관여하게 된다.
학습 초반에, 대부분의 deep normalized ResNet의 residual blocks는 skip connection에 지배된다 ⇒ residual block의 함수는 identity로 편향된다
또한 일반적으로 residual block의 depth는 전체 residual block 수인 에 비례하므로, BN은 residual branch를 the order of 의 factor로 downscale한다.
forward pass에서 factor 로 downscale된다면 backpropagation에서도 마찬가지이다.
<주장을 증명하기 위한 실험>
appendix B의 실험에 사용한 network detail
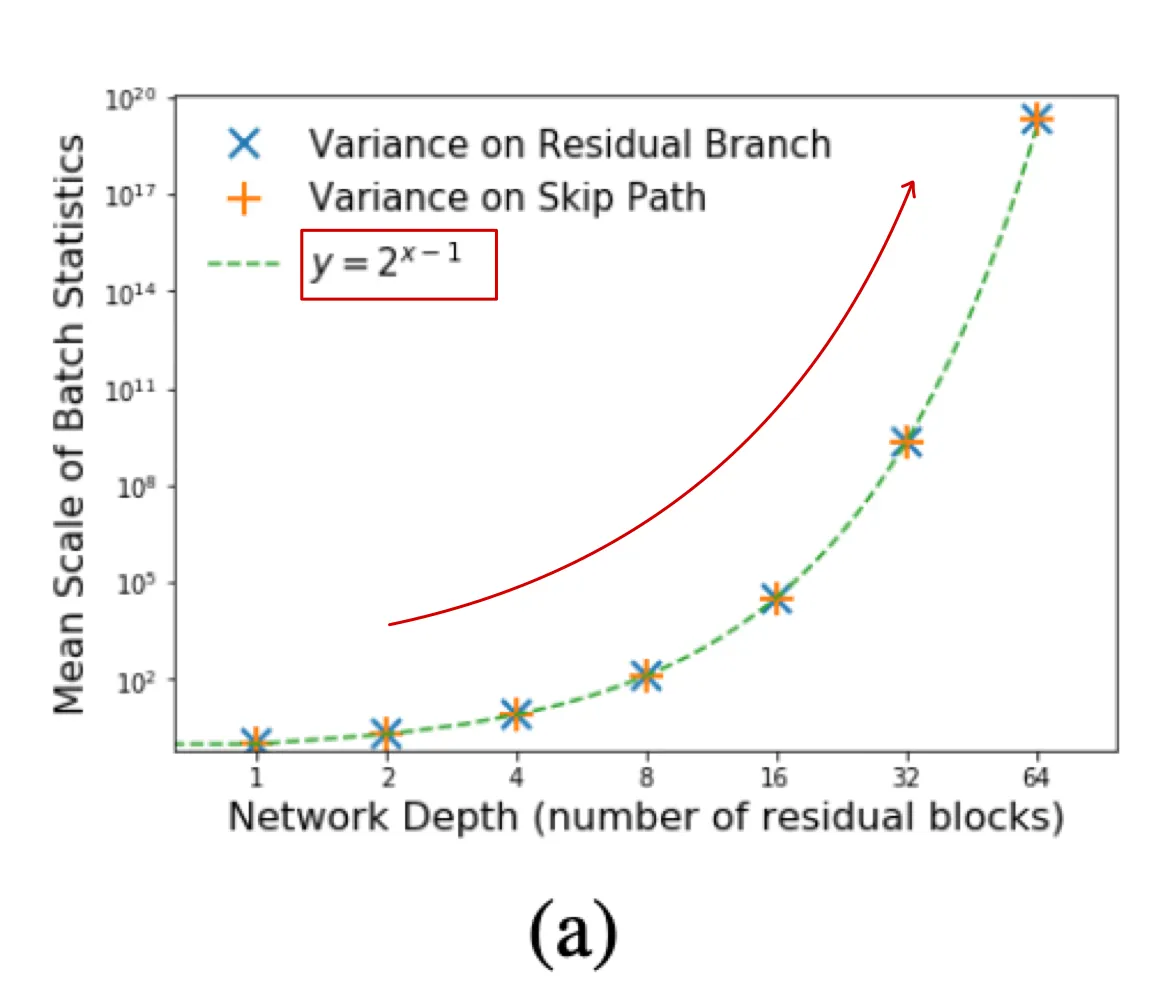
(a) : fully connected linear unnormalized residual network ( residual branch의 variance=)
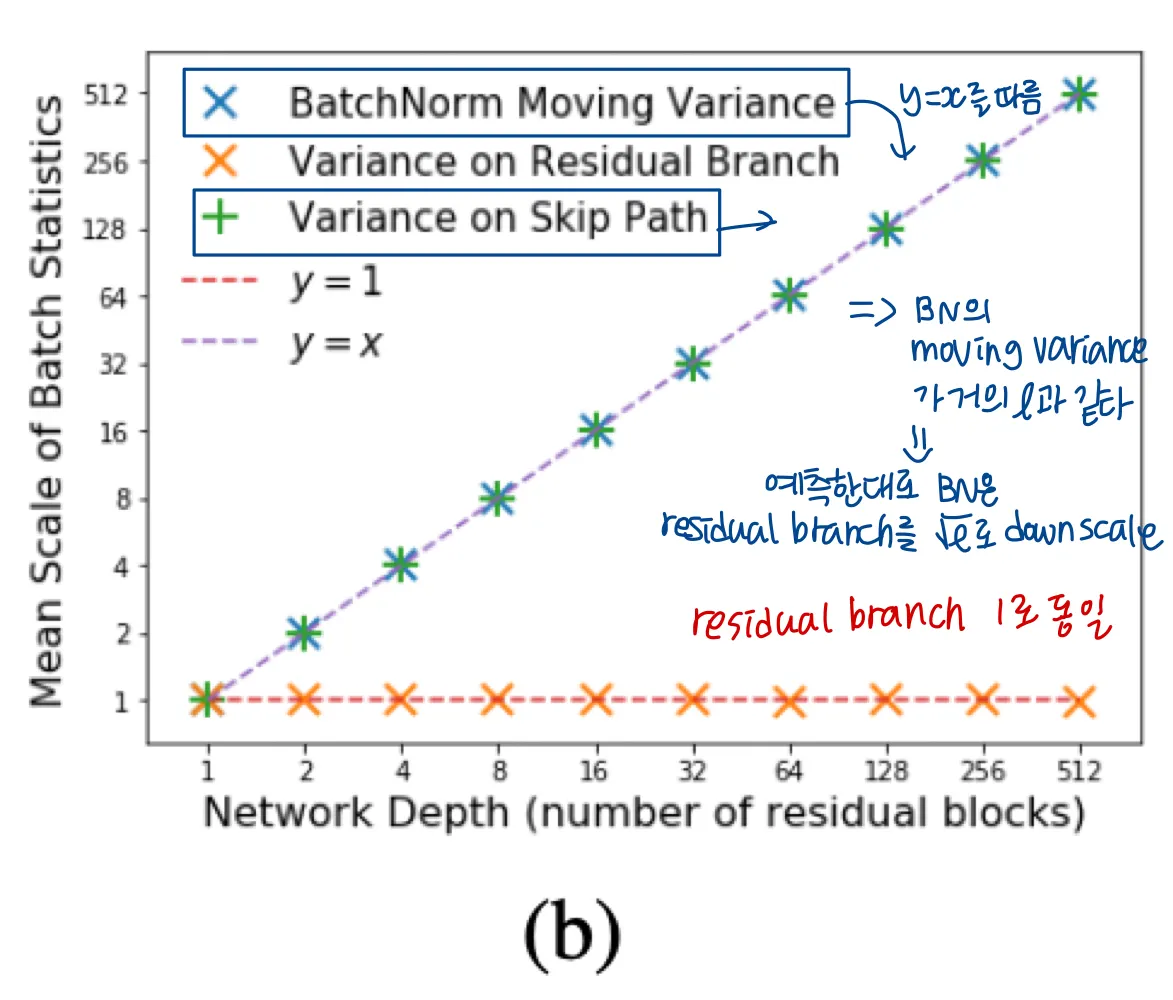
(b) : fully connected linear normalized residual network ( 번째 residual block의 skip path의 variance = , 각 residual branch의 끝의 variance )
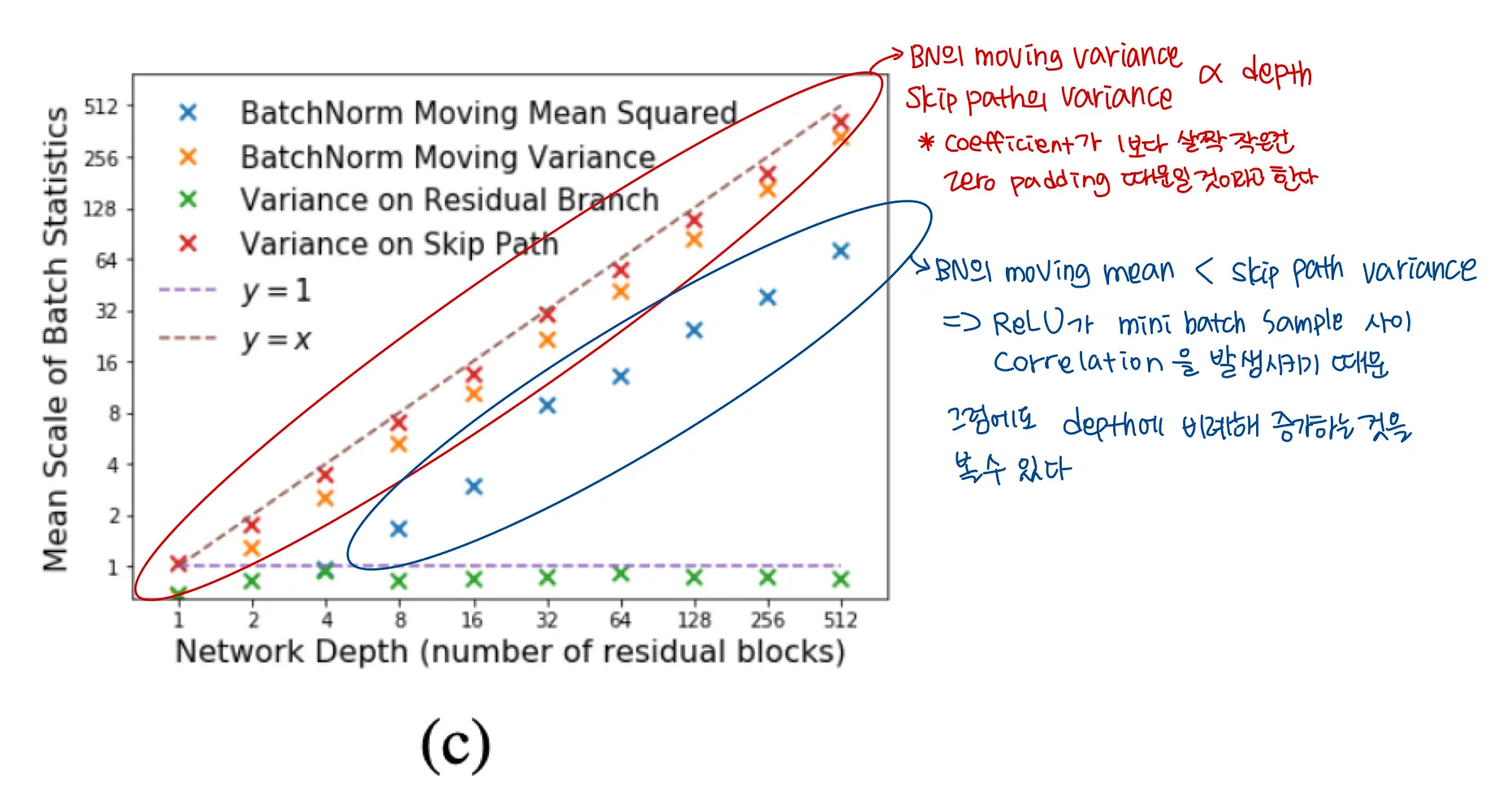
(c) : normalized convolutional residual network with ReLU activations
SkipInit : an initialization scheme to verify our analysys : 이들의 이론을 뒷받침하는 초기화 방식이다.
앞에서 주장하는 바로는 BN이 deep residual network를 학습 가능하게 하고, 그 이유는 residual branch가 학습 초기에 normalizing factor로 downscale되기 때문이라는 것이었다 ( the order of 로
SkipInit : Include a learnable scalar multiplier at the end of each residual branch, initialized to
이 section에서는 가 혹은 더 작은 값으로 초기화되었을 대 d개의 residual blocks를 가진 deep residual network가 잘 학습될 수 있음을 보여준다.
저자는 를 0으로 초기화 하는 것을 추천한다고 한다. 그래야 block이 학습 초기 identity function에 가까워지기 때문이다.
이 방식은 적용하기 더 심플하고, network depth에 관계없이 적용가능한 initialization이다.
An empirical study of residual networks at a wide range of network depths
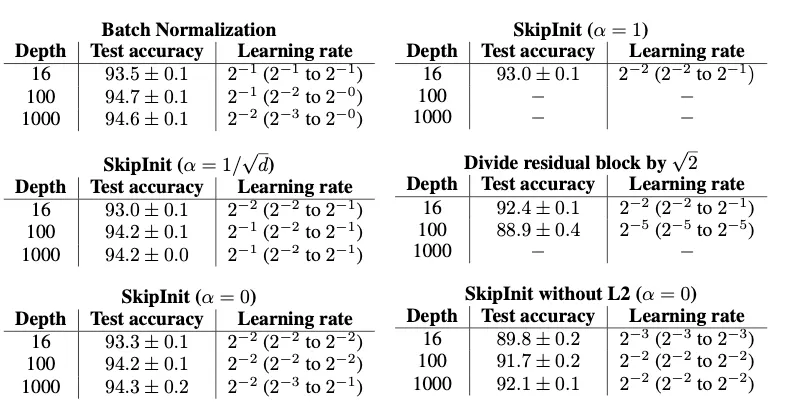
Table 1
n-2 Wide-ResNet을 이용한 실험. CIFAR-10, 200epoch, batchsize 64, depth n(between 16 and 1000)
각 depth에서 logarithmic grid의 learning rate 범위에 대해 네트워크를 7번 훈련하고, 최상의 5개 run에 대한 테스트 정확도의 평균과 표준 편차를 측정한다(이 절차는 우리의 결과가 이상치 또는 실패한 런에 의해 손상되지 않도록 보장한다)
optimal test accuracy는 mean test accuracy가 가장 높은 leaning rate에서의 평균 성능이다.
m=0.9의 SGD with heavy ball momentum 사용
learning rate는 100 epoch동안 동일하게 유지하고 이후로는 10 epoch마다 2로 나눔
image standarization, padding, random crops, left-right flips의 augmentation 적용
L2 regularization with a coefficient of
convolution layer는 He initialization 적용
위에서는 최소한의 conponents로 실험을 하였고, 이 section에서는 좀 더 실증적인 실험을 보여준다.
예상했듯 batch normalized Wide-ResNets는 넓은 범위의 depth에서 학습이 가능했고, optimal learning rate는 depth에 약간 의존적이었다.
SkipInit으로 normalization 없이 같은 효과가 가능하고, 이는 BN이 residual blocks를 skip path에 편향되게 해 deep residual network를 학습 가능하게 한다는 주장을 supoort한다.
normalized network처럼 Skipinit 사용시의 optimal learning rate는 거의 network depth에 독립적이다.
SkipInit은 모든 depth에서의 test accuracy에서 BN보다 떨어지지만, loss는 유사하다
[Table 1에서 알 수 있는 것]
•
SkipInit에서 를 1로 하면, deep residual network를 학습할 수 없었다. (논문의 주장을 뒷받침해주는 결과이다)
•
residual block의 output을 로 곱해주어 forward pass에서 activations가 explode하지 않게 해주는 것만으로는 충분하지 않다.
즉, forward pass가 stable 하다 trainability
•
→ weights가 초기에 빠르게 shrink하도록 한다.
→ 이 효과가 필요한가를 실험하기 위해 skipinit=0을 L2없이 평가해보니 필수가 아니었다
오직 residual branch의 hidden activations만 downscale하는 것으로 normalization  , weights scale
, weights scale  여도 deep network의 학습은 가능하다.
여도 deep network의 학습은 가능하다.
When can normalized networks benefit from large learning rates?
이전 연구의 주장 : BN의 최대 benefit은 conditioning of loss landscape 향상 → 큰 lr로 안정적 학습 가능
최근 논문들의 주장 : 정해진 epoch수로 학습할 때 batch size가 작으면 최적의 lr이 작다. gradient estimate의 noise에 의해 제한되기 때문이다.
이 section에서는 normalized network에서 큰 lr의 역할을 확실히 한다.
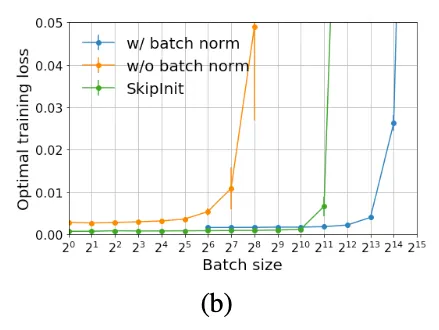
16-4 Wide ResNet trained on CIFAR-10 for 200 epohs at wide range of batch size and learning rates
•
당연히 BN이 있을 때가 가장 성능이 좋았다. 그러나 BN이 있든 없든 둘 다 small batch size(<1024)에서는 optimal test accuracy가 batch size에 관련이 없었다. ⇒ BN은 batch size가 작으면 소용없다
◦
BN이 있으면 batch size를 더 크게 학습시킬 수 있었다
•
SkipInit은 batch size <1024에서 BN이 있을 때보다 더 작은 loss를 달성했다. 그러나 batch size가 매우 커지자 unnormalized 와 유사하게 loss가 너무 커졌다
•
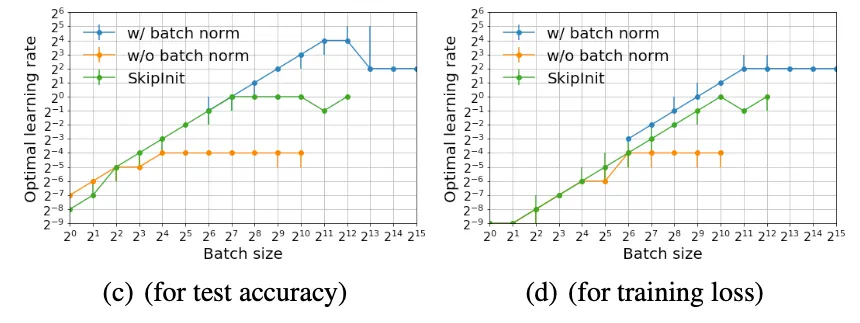
왜 BN이 큰 batch size를 가능하게 하는지 설명하기 위해 test acc를 높이고 training loss를 감소시키는 optimal learning rate를 제시했다.
◦
batch size가 작으면 optimal learning rate는 모든 방법에서 batch size에 비례했다. 그리고 서로 비슷하고, 작았다
◦
batch size가 크면 optimal lr은 batch size와 무관해졌다. normalized networks는 더 큰 lr을 사용했다. (이렇게 되는 지점은 network가 수렴하는 최대 안정적 learning rate에 도달할 때 발생했다)
normalized network의 최대 stable learning rate > SkipInit의 최대 stable learning rate > unnormalized network의 최대 stable learning rate
⇒ BN 적용 network가 더 큰 batch size를 사용할 수 있었던 이유
그러나 batch size가 작을 때에는 normalized / unnormalized 차이가 별로 없으므로 큰 learning rate의 이점을 얻을 수 없었다
그 외
On the regularization benefit of batch normalization
널리 알려진 BN의 regularization benefit은 전체 training set이 아닌 subset of full training set에서 batch statistics를 구하는데서 생기는 noise때문으로 많은 저자들이 생각한다.
이 benefit에 대해 연구하기 위해 다양한 batchsize로 실험을 해보았다고 한다.
normalized network의 전체 mini-batch에서의 batch statistics를 평가했다. 이 실험에서는 SkipInit방식에 deep network 학습 가능 + regularizing 장점을 가져오기 위해 Regularized SkipInit으로 업그레이드 했다
Regularized SkipInit
•
= 0 초기화
•
모든 conv 레이어에 bias 추가
•
softmax 이전에 0.6의 확률로 dropout 적용
Figure 4는 16-4 Wide-ResNet의 작은 batch size에서의 성능을 보여준다.
(batch size 1이면 BN은 instance normalization과 같다)
[Figure 4에서 알 수 있는 것]
•
normalized networks의 test acc는 처음에 batch가 커짐에 따라 같이 증가하지만 64이상이 되자 줄어든다.
•
training loss는 batch size가 1에서 2가 되면서 증가하지만 이후에는 batch size가 커짐에 따라 일정하게 감소한다. 이는 batch size가 적절하게 적용되면 batch statistics 예측에 대한 불확실성이 generalization benefit을 가진다는 의미이다.
•
SkipInit과 Regularized Skipinit의 성능은 batch size작을 때는 batch size에 독립적이었고 Regularized Skipinit은 batch size가 매우 작을 때 BN보다 더 높은 test acc를 달성했다.
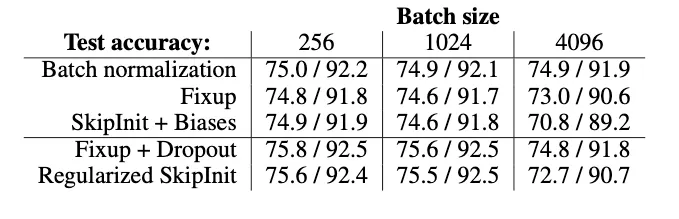
A comparison on ImageNet
ImageNet에서 BN과 SkipInit의 성능을 비교했다. + Fixup initialization까지 비교했다
Fixup initialization 절차
Discussion
이 연구에서 언급한 BN의 main benefits
1.
BN은 deep residual networks를 train 가능하게 한다.
: BN이 residual blocks를 학습 초기에 identity function의 성향을 갖도록 하기 때문이다.
이 특성이 deep residual network가 well-behaved gradients를 갖게 하고, 효과적인 학습이 가능하게 한다.
( 이는 layer normalization같은 normalization variants들과 transformer같은 다른 모델 아키텍쳐에도 해당되는 이야기 이다. )
2.
BN은 maximum stable learning rate를 증가시킨다. (batch size가 클 때만)
3.
BN은 regularizing effect가 있다.
: batch statistics를 예측하는 데에 생기는 불확실성이 generalization benefit을 준다. ( overfitting 을 방지하는 효과가 있다 )
높은 test acc를 달성하고 싶다면 필요할 수 있지만 다른 regularization을 사용해 더 높은 acc를 달성할 수도 있다는 것을 명심해야 한다.