//
Search
👍

Batch normalization

참고자료

Batch Normalization

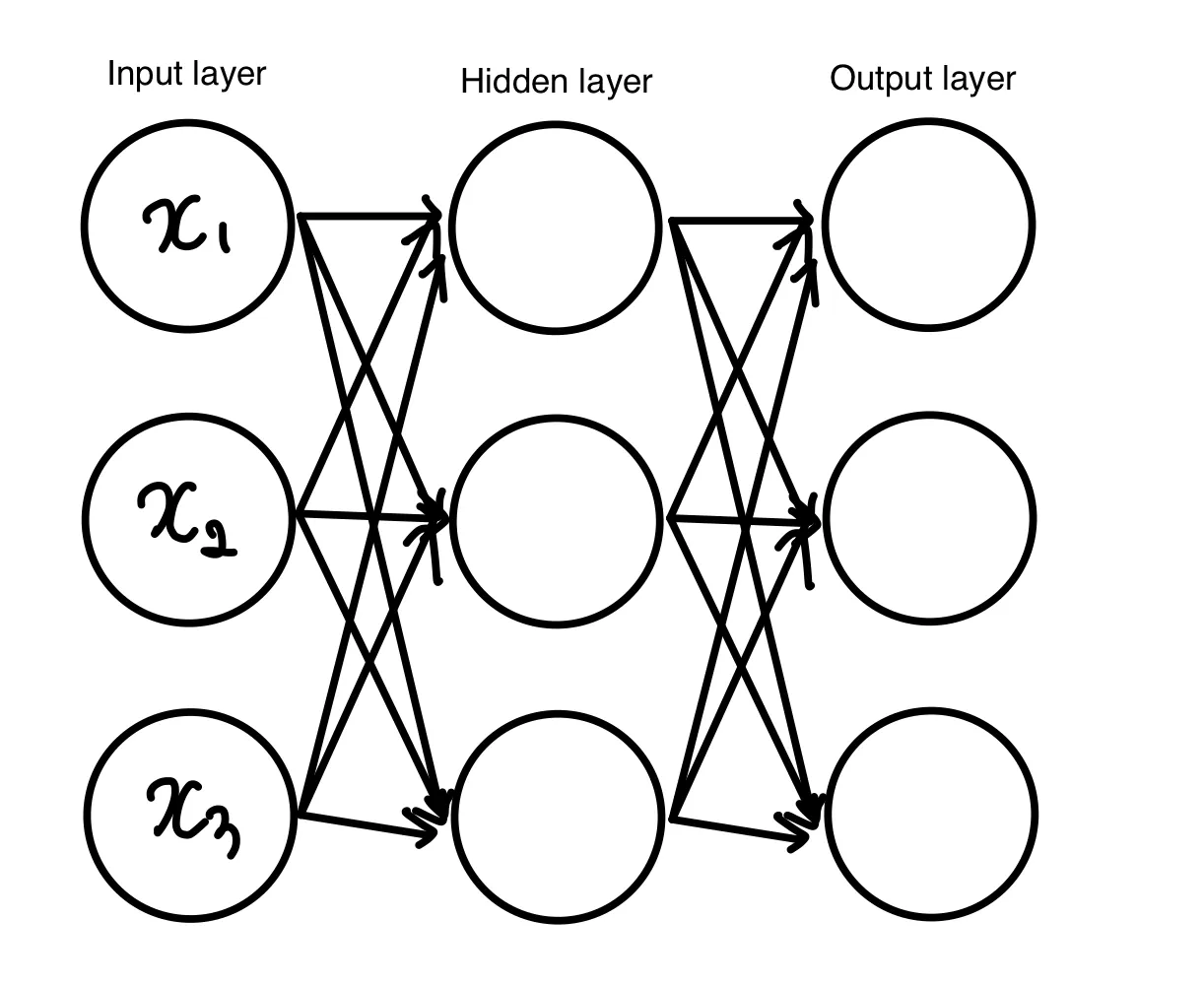
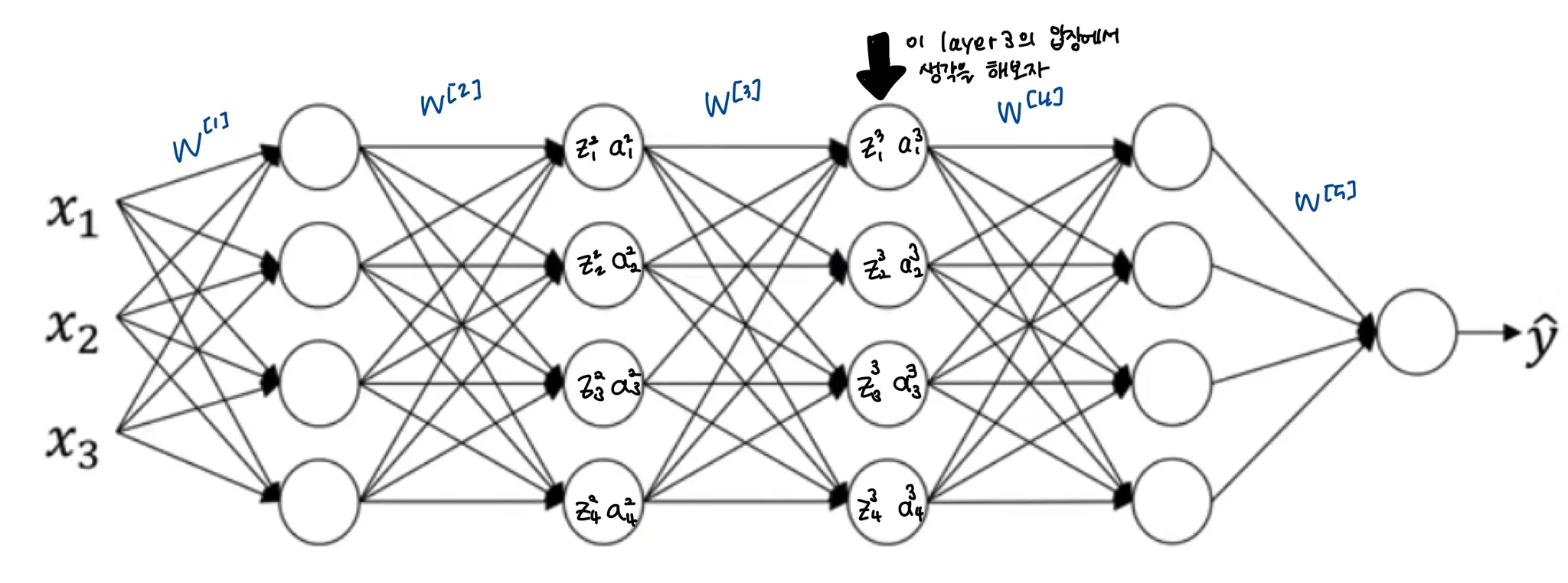
우리가 다루는 딥러닝 모델은, 하나의 레이어만을 거쳐 output이 나오지 않는다. 여러 레이어를 거쳐 output이 나오게 된다. 다음 그림은 multi layer perceptron(MLP)의 예시이다.
이러한 구조에서 레이어를 하나 더 추가하여
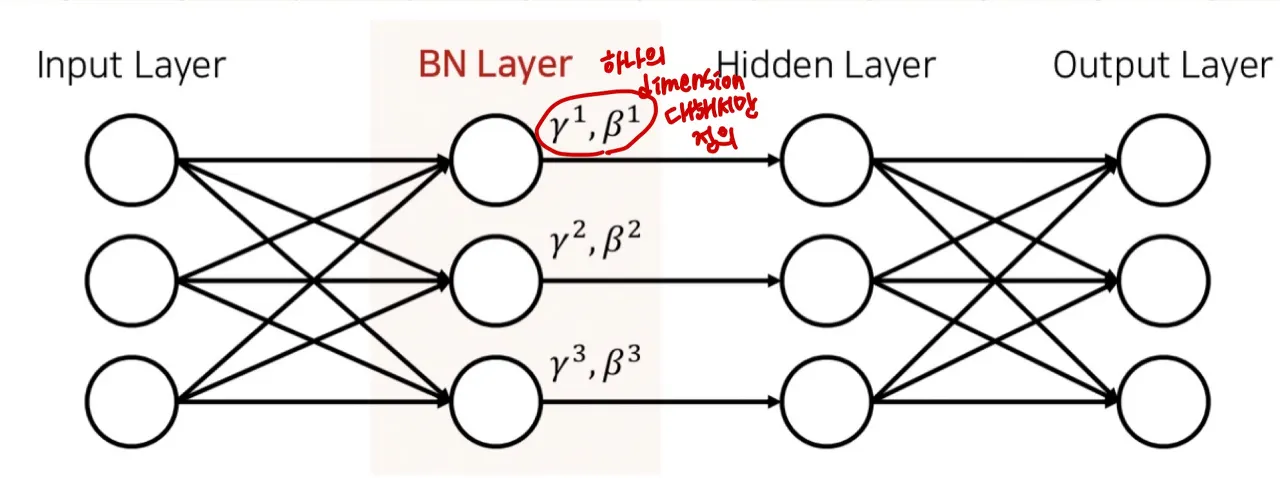
이렇게 구성하여 한 레이어에서 다음 레이어로 전달되는 중간 features도 normalization해주자는 것이 batch normalization이다. 앞의 레이어의 output이 다음 layer의 학습에 영향을 주기 때문에, 중간 features도 normalize하여 학습이 더 잘 되도록 만들어주면 좋을 것이다.
일단 batch normalization 논문에서 말하는 연구의 목적은 Gradient Vanishing / Gradient Exploding 방지 이다.
이전에는 Activation 함수의 변화 (ReLU 등), Careful Initialization, small learning rate 등으로 해결했으나, 이러한 간접적인 방법보다는 ” training 하는 과정 자체를 전체적으로 안정화하여 학습 속도를 가속시킬 수 있는 근본적인 방법 찾기 “ 가 목적인 연구이다.
https://arxiv.org/abs/2002.10444 논문에서 정리한 batch normalization의 benefit은 다음과 같다
1.
BN은 deep residual networks를 train 가능하게 한다.
2.
BN은 maximum stable learning rate를 증가시킨다. (batch size가 클 때만)
3.
BN은 regularizing effect가 있다.
이에 대한 자세한 설명은 뒤쪽에서 하겠다

BN algorithm

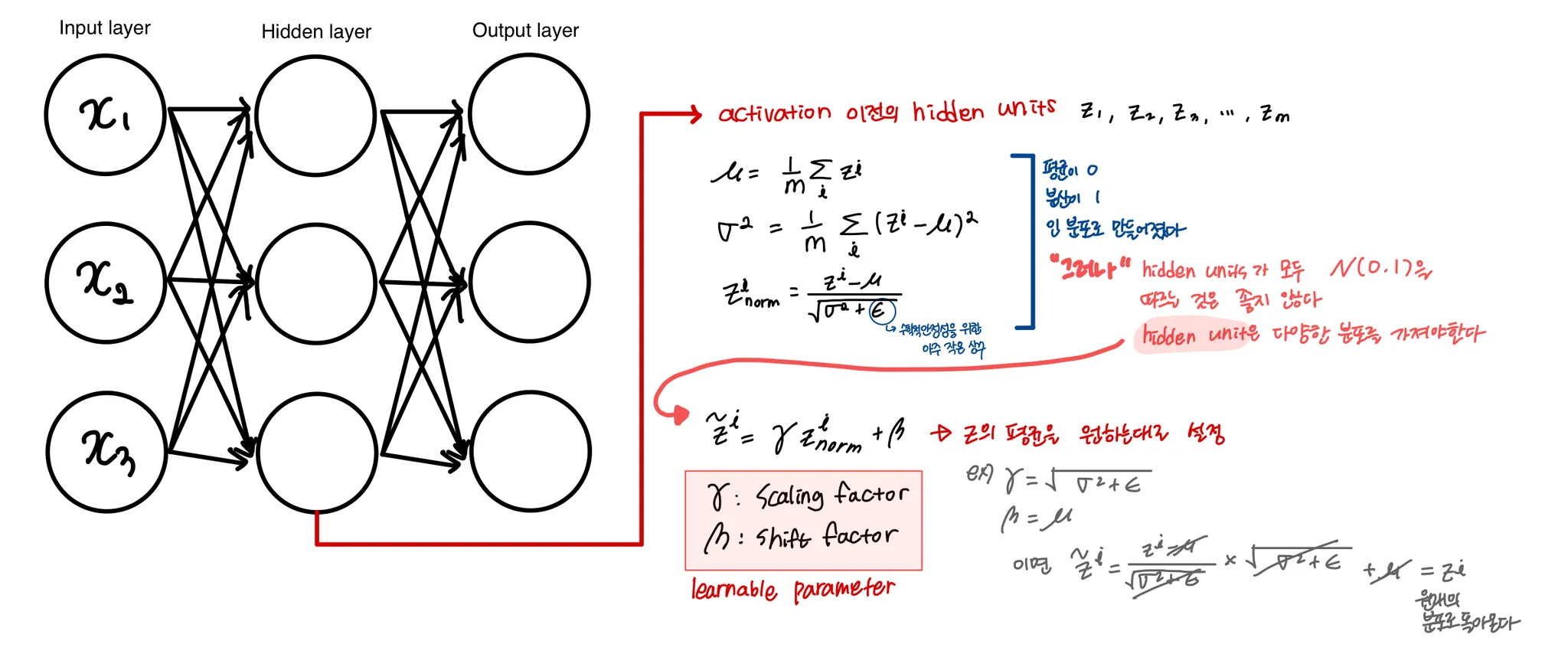
hidden unit이 다양한 분포를 가져야 하는 이유
 정리하자면, hidden unit값이 특정한 평균과 분산을 갖도록 normalize되는 것이다. 그 특정한 평균과 분산은 γ\gamma와 β\beta가 학습을 통해 결정하게 된다.

BN이 어떻게 적용되는가, backpropagation

왜 batch normalization인가?

1.
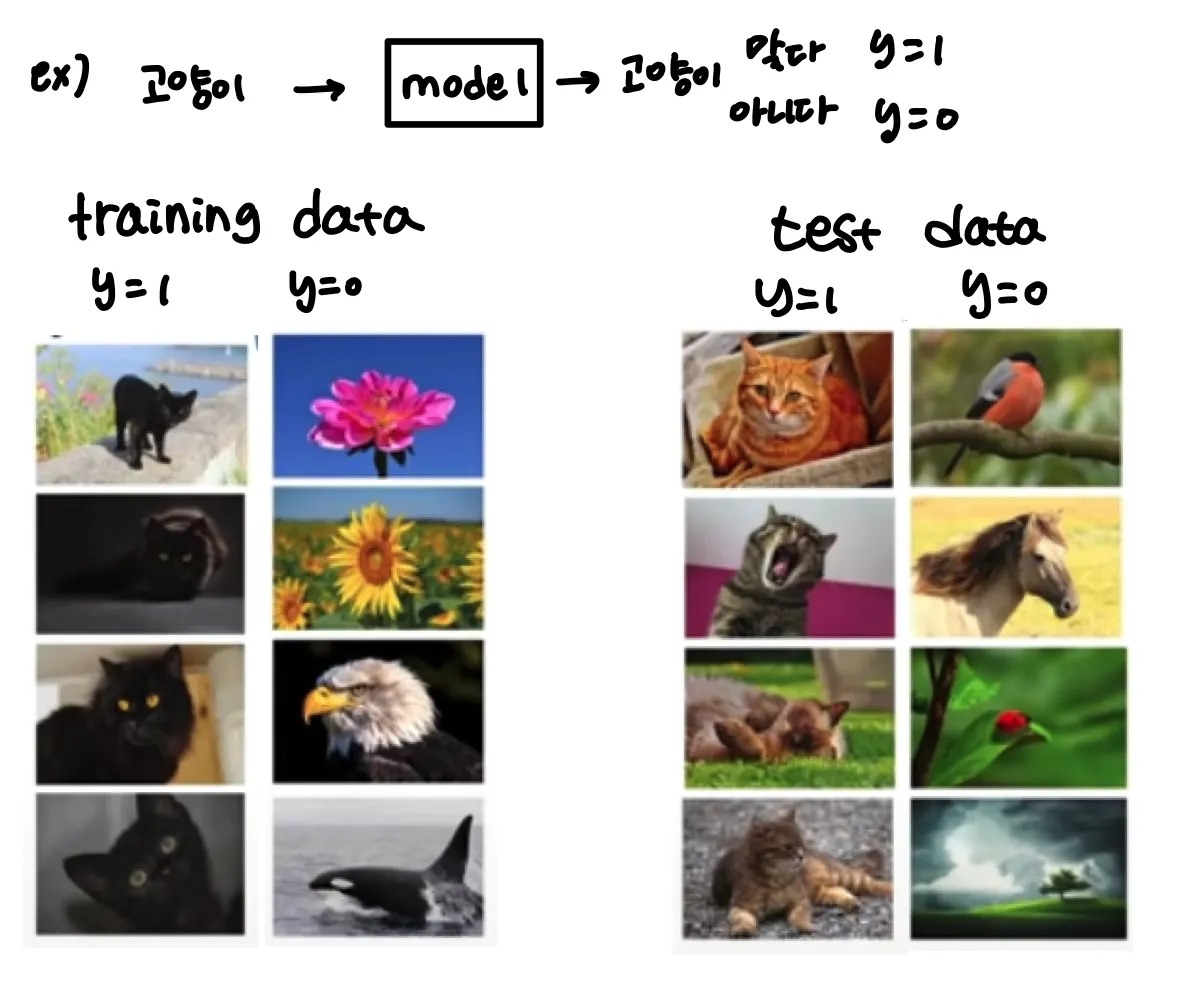
Covariant Shift 방지
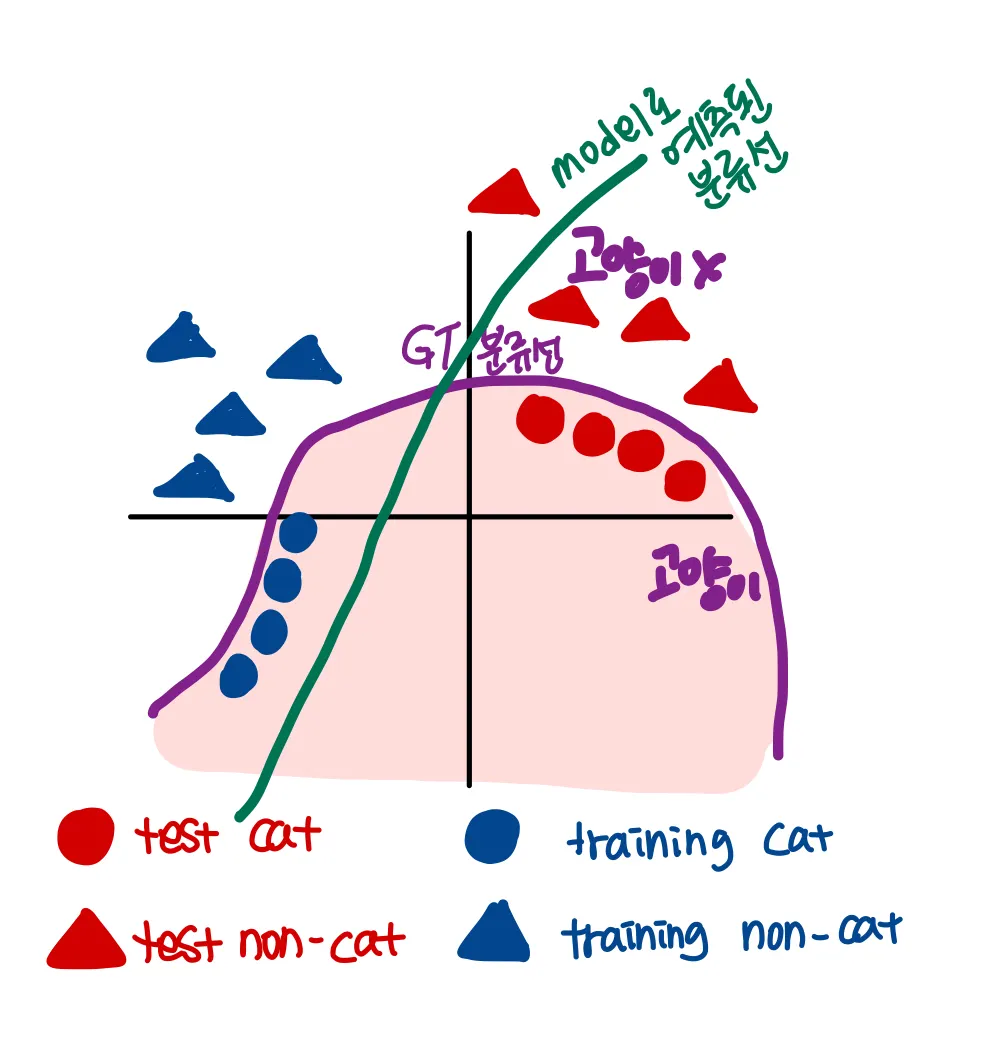
만약 이렇게 고양이를 검은색 고양이 데이터만 있는 training data로 학습을 한다면
이렇게 되버리는 현상이 발생할 수 있다. 예를 들면 검정색이면 다 고양이로 인식해버리는 것이다.
이렇게 training dataset 과 test dataset의 분포가 다른 것 처럼 데이터의 분포가 이동하는 것을 Covariant Shift ( 공변량 변화 ) 라고 한다 . Batch normalization 논문에서는 이를 학습의 불안정성의 원인이라고 판단했다.
예시로 든 상황처럼 X데이터의 분포가 변해버린다면 학습을 다시 시켜야 한다는 것이다.
고양이와 고양이가 아닌 것을 분류하는 함수인 것은 동일하나 고양이라는 큰 범주의 분포 내에서 X의 분포는 이동해버렸기 때문이다.
이를 neural network로 적용해서 다시 생각해보면
layer3에서는W[3] W^{[3]}을 y^\hat{y}를 잘 예측할 수 있도록, 즉 W[4]와W[5] W^{[4]}와 W^{[5]} 도 잘 학습될 수 있도록 최적화한다. 앞의 레이어들의 값인 Z[1],Z[2],a[1],a[2]Z^{[1]}, Z^{[2]}, a^{[1]}, a^{[2]} 로부터 y^\hat{y} 를 예측하는 것이다.
만약 앞의 weights인 W[1],W[2]W^{[1]}, W^{[2]}가 업데이트 됨에 따라서 Z[1],Z[2],a[1],a[2] Z^{[1]}, Z^{[2]}, a^{[1]}, a^{[2]} 의 분포가 변한다면, 즉 covariant shift가 발생한다면, layer3은 또 다시 새롭게 학습을 해야한다. BN 논문에서는 이를 학습 불안정성의 문제로 제시하고, BN을 통해 hidden layer들의 분포의 변화를 제한해 준 것이다.
 Z[2]Z^{[2]} 의 값이 변하더라도, 평균과 분산은 γ\gamma와 β\beta가 정해주는 대로 유지될 것이라는 것이다. 앞선 레이어의 값이 바뀌었을 때, 세 번째 레이어가 받아들여 학습하게될 값의 분포를 제한해 covariant shift의 문제를 해결
또한 이는 각 레이어들 간의 연관성을 줄여 학습이 더 잘 되도록 하는 효과도 있다
1번 benefit인 deep residual network가 train가능해지는 효과를 설명할 수 있는 부분이다.
2.
regularization 측면 (3번 generalization benefit)
BN 과정에서 연산하는 평균과 분산은 mini batch 내에서 연산하기 때문에 전체 training data의 statistics와는 차이가 있다. 즉, noise가 있는 평균과 분산을 사용한다.
regularization을 위해 사용하는 Dropout과 비교하면, dropout은 확률에 따라 hidden layer에 0 혹은 1을 곱한다. 이 때문에 multiplication noise를 갖게된다.
BN은 표준편차로 나누는 과정에서 multiplication noise를, 평균을 빼는 과정에서 addition noise를 갖게된다. 또한 평균과 표준편차 자체도 noise를 가지고 있기에 dropout과 같이 regularization효과를 갖게된다.
왜 ? noise는 뒤의 hidden layer들이 하나의 hidden layer에 너무 의존하지 않도록 만들어주기 때문이다
그러나 batch size가 너무 커지면 ( 64 → 512 처럼 ) 더 큰 데이터에서 평균 및 분산을 연산하게 되므로 이 효과가 떨어질 수 있다. 따라서 이를 BN의 주 목적으로 사용하면 안된다

Test time에서의 BN

test시에는 학습 때와 달리 한가지 샘플씩 inference한다. 따라서 training 시의 BN과는 다를 수 밖에 없다.
[BN에서 사용되는 식들]
•
μ=1m∑iz(i)\mu = \frac{1}{m} \sum_{i} z^{(i)}
•
σ2=1m∑i(z(i)−μ)2\sigma^2 = \frac{1}{m} \sum_{i} (z^{(i)}-\mu)^2
•
znorm(i)=z(i)−μσ2+ϵz_{norm}^{(i)} = \frac{z^{(i)}-\mu}{\sqrt{\sigma^2 + \epsilon}}
•
z~(i)=γznorm(i)+β\widetilde{z}^{(i)} = \gamma z_{norm}^{(i)} + \beta
하나의 샘플 내에서 평균 / 분산을 구한다는 것은 말이 안된다.
 여러 mini-batch 걸쳐 구한 Exponentially Weighted Moving Average ( 지수 가중 평균 ) 사용
σ2\sigma^2에 대해서도 비슷한 방식으로 추정할 수 있다.
== μ\mu와 σ2\sigma^2의 moving average를 구함⇒ μ\mu와 σ2\sigma^2가 학습과정에서 가졌던 값들을 추정하는 것이다.
이 값을 가지고znorm(i) z_{norm}^{(i)}를 계산한다. 그리고 학습된 γ\gamma와 β\beta 를 가지고 z~(i)\widetilde{z}^{(i)} 를 계산하면 된다.

BN for CNN

위에서 다룬 MLP말고, CNN에 대해서 적용시켜보면 다음 그림과 같이 나타낼 수 있다.
Batch Normalization을 CNN에 적용시키고 싶을 경우
•
convolution layer에서 activation function에 값을 넣기 전 보통 Wx+b 형태로 weight를 적용시키는데, Batch Normalization을 사용하면 normalize 할 때 beta 값이 b의 역할을 대체할 수 있기 때문에 b를 없애준다.
•
convolution의 성질을 유지시키고 싶기 때문에, 각 channel을 기준으로 각각의 Batch Normalization 변수들을 만든다.
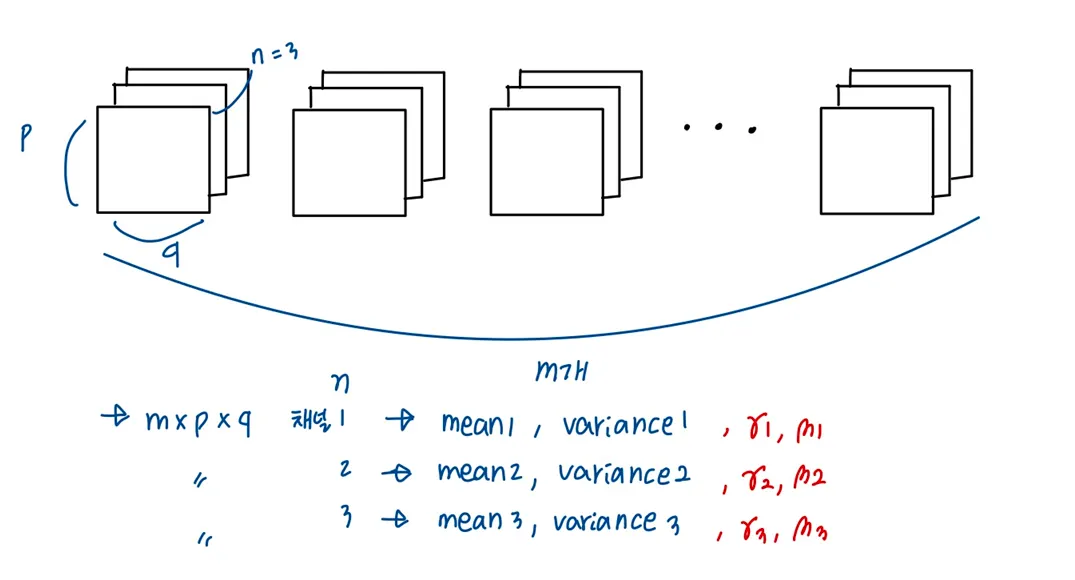
ex) m의 mini-batch-size, n의 channel size 를 가진 Convolution Layer에서 Batch Normalization을 적용
convolution을 적용한 후의 feature map의 사이즈가 p x q 일 경우, 각 채널에 대해 m x p x q 개의 각각의 스칼라 값에 대해 mean과 variance를 구하는 것이다. 최종적으로 γ\gamma와 β\beta는 각 채널에 대해 한개씩 해서 총 2n개의 독립적인 Batch Normalization 변수들이 생기게 된다.
Made with