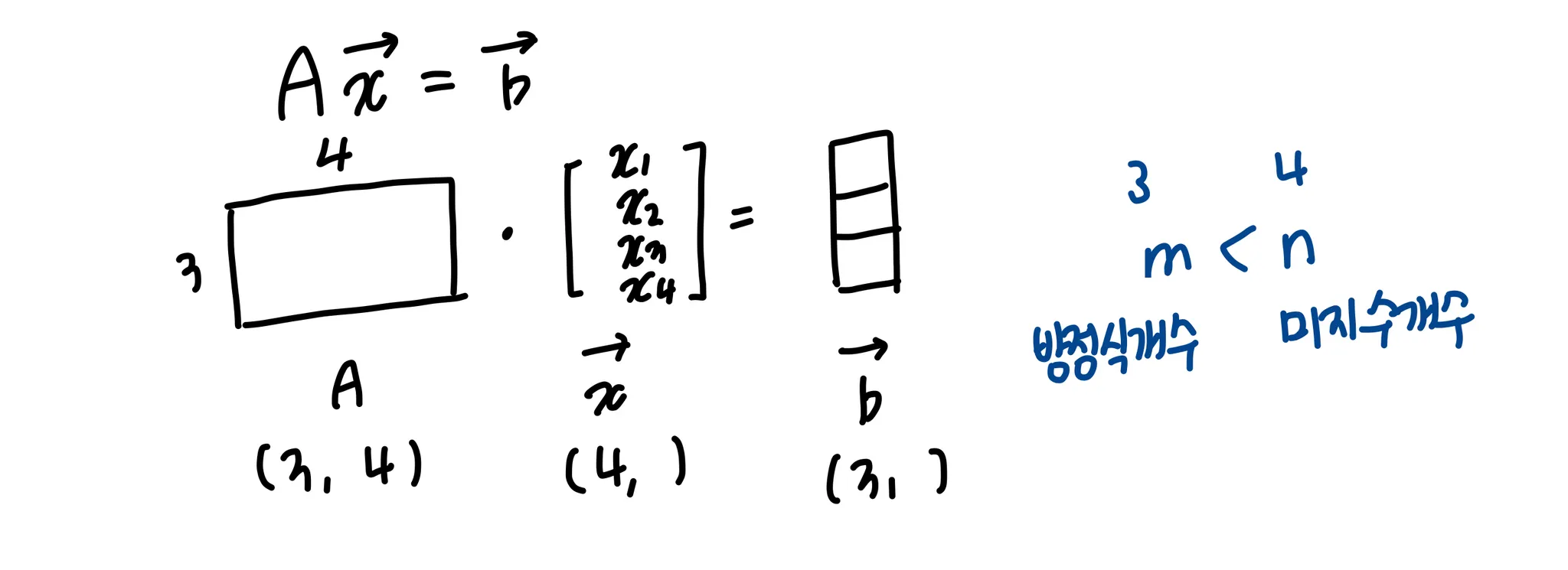
선형 결합 / vector equation / matrix multiplication의 다양한 관점 에서 다음과 같은 vector equation의 해는 가 에 속해야 존재한다고 했다.
그렇다면 해가 하나만 존재하는지는 어떻게 알 수 있을까?
답을 먼저 말하자면 이 선형 독립 (linearly independent)이어야 해가 유일하다.
반대로 선형 종속(linearly dependent)이면 해는 무수히 많다.
선형 독립과 선형 종속에 대해 조금 더 자세히 알아보자.
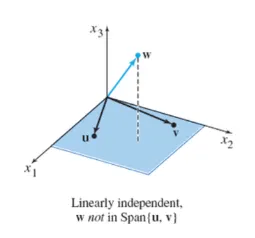
선형 독립 (Linear Independence)
선형독립의 정의는 다음과 같다.
벡터집합 와 실수 가 주어졌을 때 을 만족하는 해가 으로 유일할 때 주어진 벡터 집합은 선형독립이라고 한다.
이를 좀 더 직관적으로 표현하면
•
부터 벡터를 하나씩 추가한다고 생각했을 때, 지금 추가할 벡터 가 에 속하지 않는다는 것이다.
•
즉 벡터 집합 내의 어떠한 원소도 나머지 원소들의 선형결합으로 나타낼 수 없다.
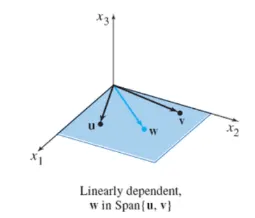
선형 종속 (Linear Dependence)
선형 종속은 그 반대라고 생각하면 된다.
벡터집합 와 실수 가 주어졌을 때 을 만족하는 해가 외의 해가 존재할 때 주어진 벡터 집합은 선형종속이라고 한다.
•
부터 벡터를 하나씩 추가한다고 생각했을 때, 지금 추가할 벡터 가 에 속함
세 벡터의 span이 같은 평면
•
벡터 집합 내의 원소 중 적어도 하나는 나머지 원소들의 선형 결합으로 나타낼 수 있다.
n차원 벡터들이 n개 보다 많이 주어진다면 해당 벡터 집합은 선형 종속이다.
⇒ n=3이라고 생각을 했을 때,
첫번째 벡터를 추가했을 때 그 span은 line이다.
두번째 벡터를 첫번째 벡터에 독립이도록 추가했을 때 두 벡터의 span은 평면이다.
세번째 벡터를 나머지 두 벡터에 독립이 되도록 추가했을 때 세 벡터의 span은 3차원 공간이다.
4번째 벡터를 3차원 공간을 벗어나도록 추가 할 수가 없다.
⇒ 이는 방정식 개수보다 미지수의 개수가 많으면 해가 무수히 많다는 개념으로 이어진다.
선형 종속인 벡터들은 span을 증가시키지 않는다.
로 표현할 수 있기 때문에
결국 세 벡터의 선형결합은 과 의 선형결합으로 나타낼 수 있다.
따라서
이면 이다.