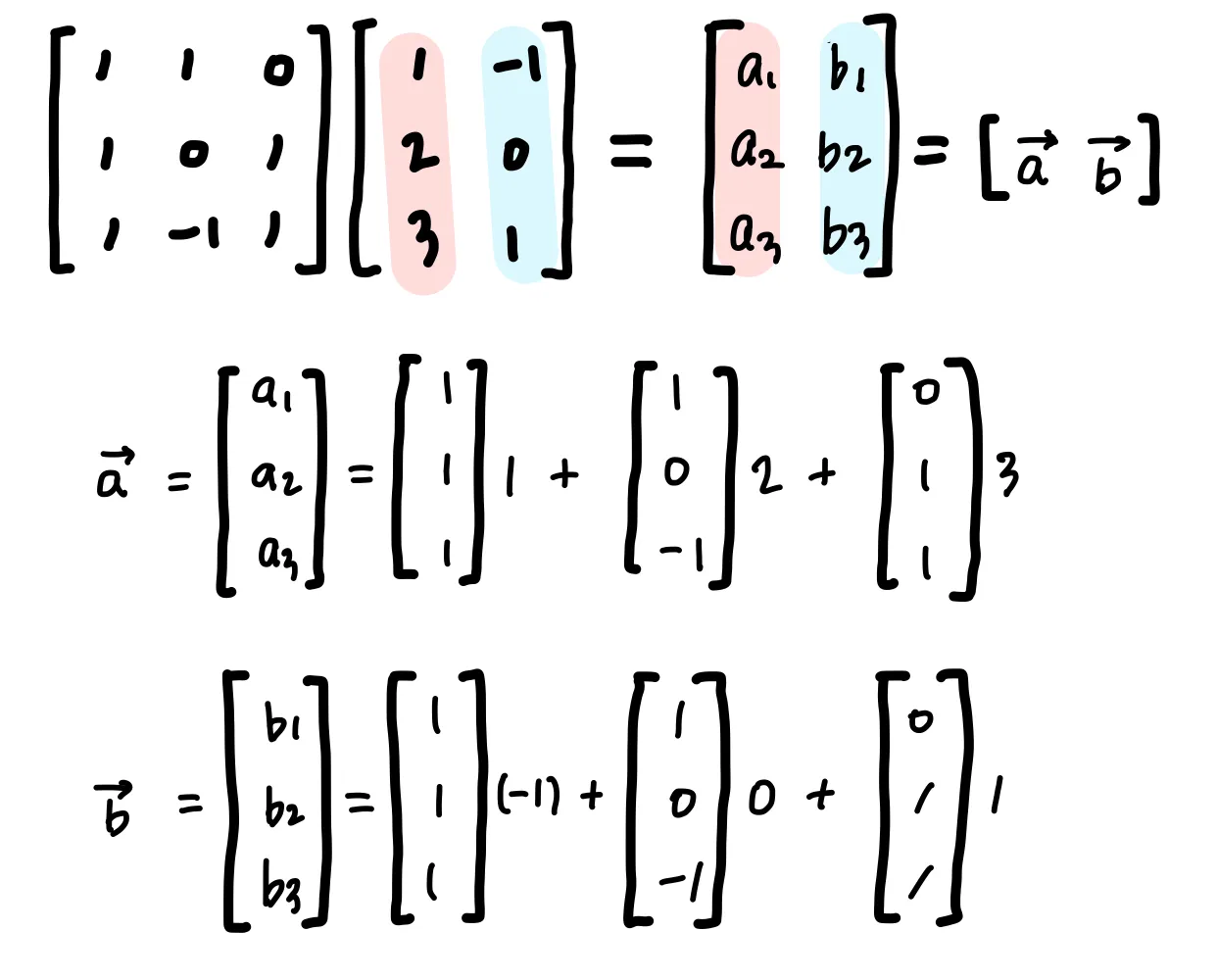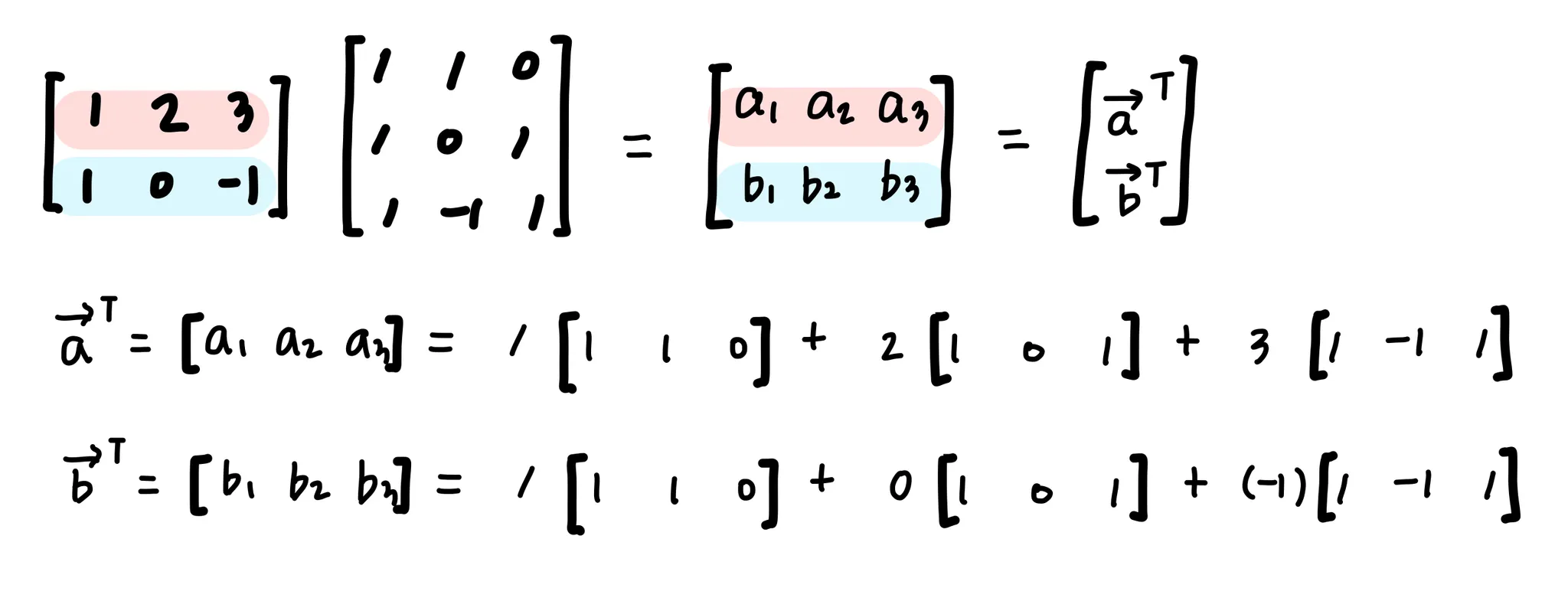Search

선형 결합 / vector equation / matrix multiplication의 다양한 관점

※ 주재걸 교수님의 인공지능을 위한 선형대수 강좌를 기반으로 작성되었습니다

선형결합 (Linear Combinations)

주어진 벡터 v1,v2,...,vp\bold{v}_1, \bold{v}_2, ...,\bold{v}_p in Rn\mathbb{R}^n 와 스칼라 c1,c2,…,cpc_1, c_2, … , c_p에 대해
c1v1+c2v2+c3v3+...+cpvpc_1\bold{v}_1+c_2\bold{v}_2 + c_3\bold{v}_3 + ... + c_p\bold{v}_p
를 v1,v2,...,vp\bold{v}_1, \bold{v}_2, ...,\bold{v}_p의 coefficients c1,c2,…,cpc_1, c_2, … , c_p와의 linear combiation이라 한다.
•
coefficients는 weights라고 할 수도 있으며, 스칼라값이다. zero를 포함한 모든 실수가 가능하다.
•
coefficients가 스칼라값이기에 선형결합의 결과도 ∈Rn\in \mathbb{R}^n

matrix equation을 vector equation으로 표현하기

personID
weight (kg)
height (ft)
is_smoking
life-span (year)
1
60
5.5
1
66
2
65
5.0
0
74
3
55
6.0
1
78
[605.51655.00556.01][x1x2x3]=[667478]\begin{bmatrix} 60&5.5&1 \\ 65&5.0&0 \\ 55&6.0&1\end{bmatrix}\begin{bmatrix} x_1\\x_2\\x_3\end{bmatrix} = \begin{bmatrix} 66 \\ 74 \\ 78 \end{bmatrix}는 matrix equation Ax=bA\bold{x} = \bold{b}이다.
이는 vector equation (벡터방정식)으로 변환될 수 있다
[606555]x1+[5.55.06.0]x2+[101]x3=[667478]\begin{bmatrix} 60\\65\\55\end{bmatrix}x_1+\begin{bmatrix} 5.5\\5.0\\6.0\end{bmatrix}x_2+\begin{bmatrix} 1\\0\\1\end{bmatrix}x_3 = \begin{bmatrix} 66\\74\\78\end{bmatrix}
⇒
60x1+5.5x2+1x3=6660 x_1 + 5.5x_2+ 1x_3 = 66 66x1+5.0x2+0x3=7466 x_1 + 5.0x_2+ 0x_3 = 74 55x1+6.0x2+1x3=7855 x_1 + 6.0x_2+ 1x_3 = 78
이는 다음과 같은 선형결합의 형태로 볼 수 있다
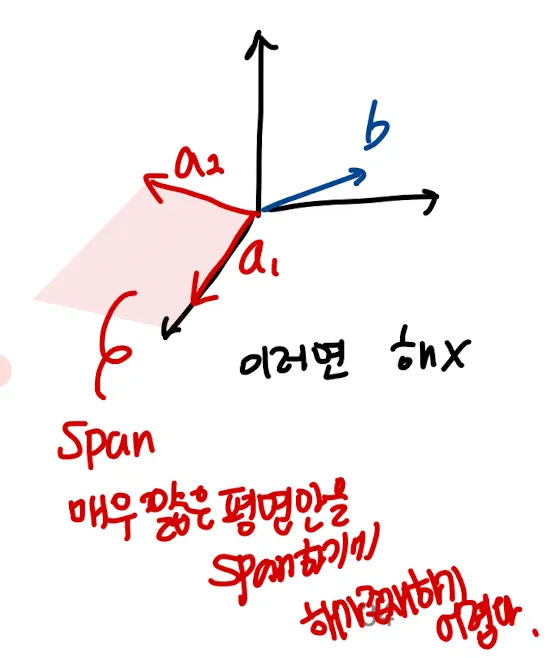
a1x1+a2x2+a3x3=b\bold{a}_1 x_1 + \bold{a}_2 x_2 + \bold{a}_3 x_3 = \bold{b}
이 vector equation을 고려했을 때 Ax=bA\bold{x} = \bold{b} 의 해는 언제 존재한다고 할 수 있을까?

Span

이 내용에 대해서는 이전 글에서 다뤘다
•
간단히 말해 span은 n차원의 유한한 벡터 p개가 주어졌을 떄 이 벡터들의 선형집합으로 만들어지는 공간
•
c1v1+c2v2+c3v3+...+cpvpc_1\bold{v}_1+c_2\bold{v}_2 + c_3\bold{v}_3 + ... + c_p\bold{v}_p 의 형태로 나타낼 수 있는 모든 벡터들의 모임
•
따라서 span은 n차원 공간의 부분집합이 된다
이전에 다룬 내용이기에 이정도만 설명한다

Vector Equation의 Geometric Interpretation

[606555]x1+[5.55.06.0]x2+[101]x3=[667478]\begin{bmatrix} 60\\65\\55\end{bmatrix}x_1+\begin{bmatrix} 5.5\\5.0\\6.0\end{bmatrix}x_2+\begin{bmatrix} 1\\0\\1\end{bmatrix}x_3 = \begin{bmatrix} 66\\74\\78\end{bmatrix}
a1x1+a2x2+a3x3=b\bold{a}_1 x_1 + \bold{a}_2 x_2 + \bold{a}_3 x_3 = \bold{b}
해가 존재한다 = a1,a2,a3\bold{a}_1, \bold{a}_2, \bold{a}_3의 선형결합으로 b\bold{b}를 구할 수 있다 = b\bold{b}가 Span{a1,a2,a3}Span\{\bold{a}_1, \bold{a}_2, \bold{a}_3\}에 속해야 해가 존재한다.
a1a_1과 a2a_2만 주어진 상황으로 단순화 했을 때

Matrix Equation을 vector의 선형결합으로 살펴보기

행렬과 행렬의 곱을 앞의 행렬의 row와 뒤의 행렬의 column의 inner product로 정의했었다.

1. 왼쪽 행렬의 columns의 선형결합이라 할 수 있다.

2. 오른쪽 행렬의 row의 선형결합이라 할 수 있다.

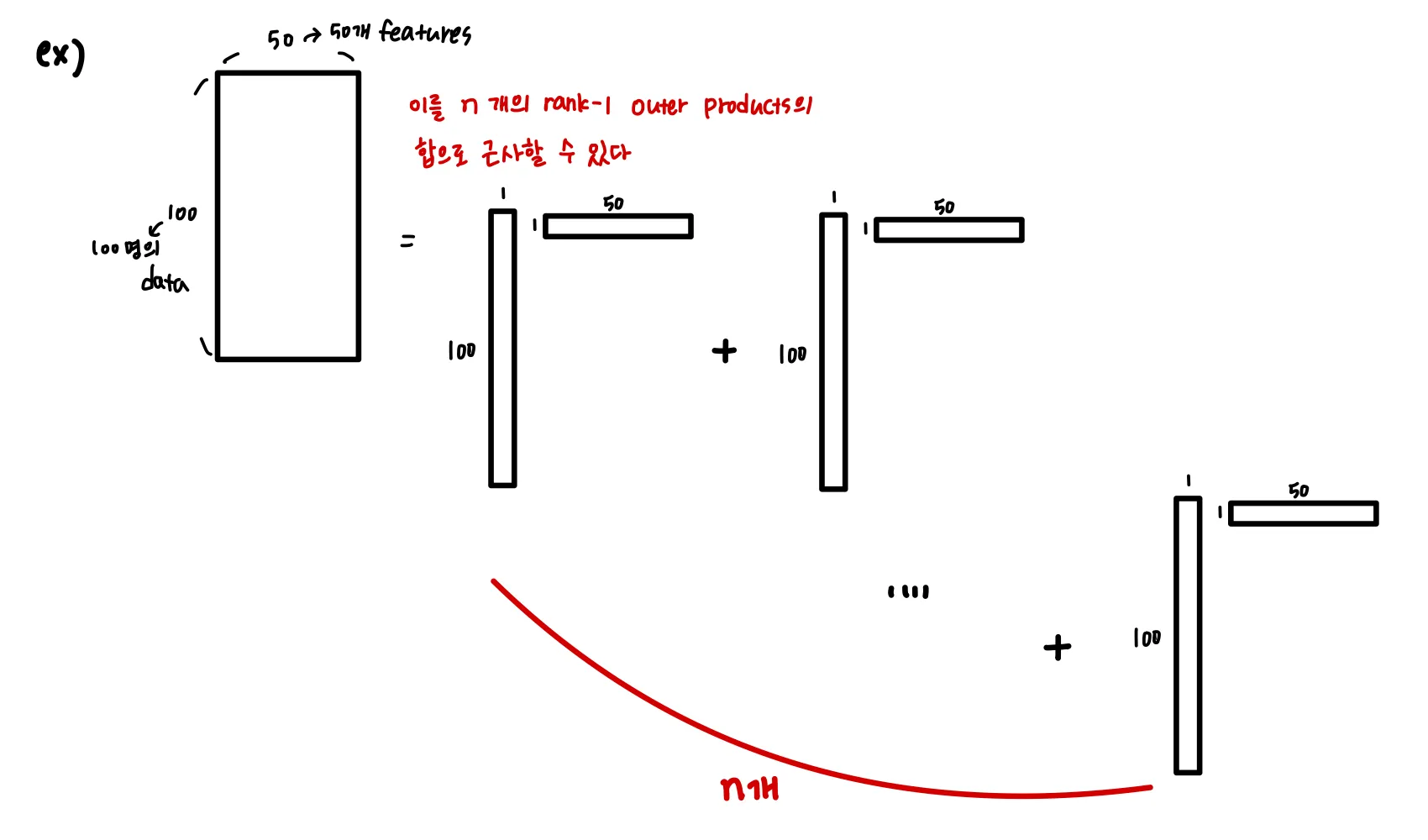
3. Sum of (Rank-1) Outer Products라 할 수 있다.

이 방식이 머신러닝과 가장 가까운 해석이라고 볼 수 있다.
word2vec, PCA, singular value decomposition 등에서 이러한 관점이 사용된다.
•
covariance matrix in multivariate guassian
•
gram matrix in style transfer
⇒ 근사적 표현으로 유용한 역할을 하는 벡터들을 찾을 수 있다.
Made with