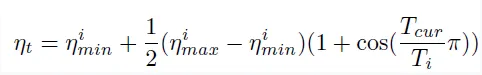Search

[lr scheduler] cosine annealing

Papers with Code - Cosine Annealing Explained
Cosine Annealing is a type of learning rate schedule that has the effect of starting with a large learning rate that is relatively rapidly decreased to a minimum value before being increased rapidly again.
https://paperswithcode.com/method/cosine-annealing
arxiv.org
https://arxiv.org/pdf/1608.03983v5.pdf

Learning rate란 ..

learning rate의 개념은 optimization에서 나온다
loss function / objective function을 optimizing 할 때 gradient descent 기반 optimization algorithm을 적용하는 경우 learning rate ( 학습률 ) η\eta 를 하나의 고정된 값으로 사용하지 않고, 학습 반복이 진행됨에 따라 정해놓은 규칙 / schedule대로 학습률을 늘리거나 줄이는 전략을 learning rate schedule / learning rate scheduler라고 한다.

lr schduler가 왜 필요할까

SGD방식의 업데이트 식
W←W−η∂L∂W\bold{W} \leftarrow \bold{W}-\eta \frac{\partial L}{\partial \bold{W}}
이 식을 따라 gradient descent의 weight update가 진행될 때 고정된 learning rate를 사용하면
•
η\eta 가 작으면 수렴속도가 느려진다. local minimum에 수렴되어버려 최적의 weight를 찾지 못한다.
•
η\eta 가 크면 local minimum은 쉽게 탈출해도 최적점( loss function의 최소지점 ) 근처에서 진동이 심해 수렴하지 못하거나 극단적인 경우 loss가 발산해버릴 수 있다.
그래서 효율적인 방식으로 local minimum은 피하면서 global minimum에 수렴하는 방법은
⇒ 학습 초기 큰 learning rate로 시작해 epoch가 진행됨에 따라 점차 줄여나가는 것.( decaying learning rate )
fixed learning rate보다 decaying learning rate가 일반적으로 더 최적점을 잘 찾아나갈 수 있다는 것이 알려져 있다.

Cosine Annealing with Warm Restart

나는 이 방식의 learning rate scheduling을 최근에 많이 사용하였다.
특히 transformer의 학습 예제 코드들을 보면 이 lr scheduler를 사용한 것을 볼 수 있다.
transformers.get_cosine_schedule_with_warmup
learning rate schedule 방식에는 여러 방식이 있다
•
power scheduling
•
exponential scheduling
•
piecewise constant scheduling
•
performance scheduling
•
1 cycle scheduling
데이터 / 모델 / task 등에 따라 어떠한 방식이 좋은지는 알 수 없다.
cosine decay는 restart를 제외하면 1 cycle scheduling과 유사하다
one-cycling scheduling
위에 나열한 방식들 중 다른 방식들은 학습률을 점점 감소시키는 방식의 scheduler들인데, one-cycle scheduling같은 경우에는 전체 학습 중 절반까지는 학습률을 선형적으로 증가시키고, 이후의 절반의 반복동안에는 학습률을 선형적으로 감소시킨다. 또한 마지막 몇 epoch동안에는 추가적으로 더 감소시킨다.
arxiv.org
https://arxiv.org/pdf/1803.09820.pdf
decay learning rate with a cosine annealing / cosine annealed warm restart learning schedule
•
warm restart : decaying하는 학습률이 주기적으로 initial value로 reset된다
•
cosine annealing : 학습률을 annealing(크게 시작해 작게 만든다)하기 위한 함수로 cosine 함수를 사용한다
논문에서 annealing에 선형함수를 사용하는 것보다는 cosine 함수를 사용하는게 더 좋은 성능을 보인다고 한다
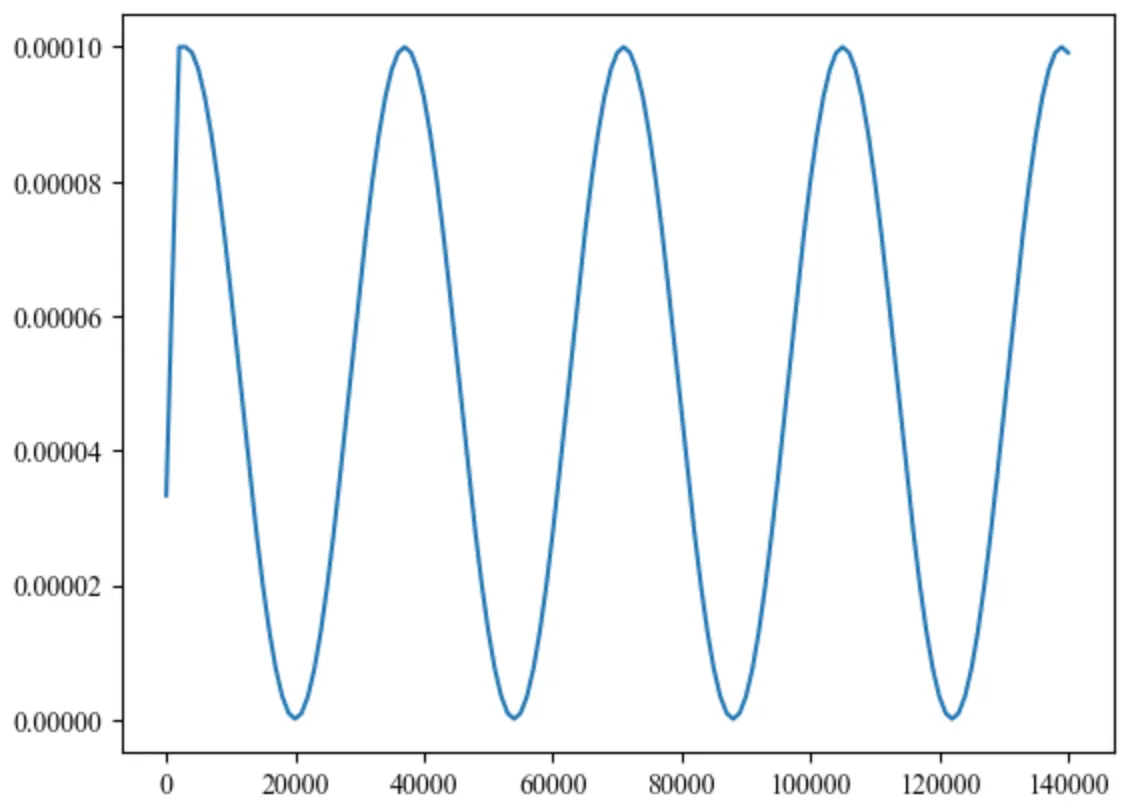
<실제로 학습에 사용했을 때 얻은 learning rate 변화 그래프>
<cosine annealing 학습률 감쇄 수식>
•
ii = annealing period
•
ηmini\eta_{min}^i , ηmaxi\eta_{max}^i : 주기별 최소 / 최대 학습률 → 주기마다 학습률 상/하한을 다르게 설정할 수 있다.
•
TiT_i : 각 주기의 step
•
TcurT_{cur} : 현재 주기에서의 iteration step
주기 ii의 tt번째 iteration에서의 학습률 ηt\eta_t 는 Tcur=0T_{cur}=0 일 때 ηmaxi\eta_{max}^i 가 되고, Tcur=TiT_{cur}=T_i일 때 ηmini\eta_{min}^i가 되어 해당 주기에 설정된 최대 학습률에서 최소 학습률까지 연속적으로 decay된다.
동일 길이 주기의 기본 annealing보다는 주기의 길이를 점차 늘리는 방법이 성능을 더 많이 향상시킨다고 한다.
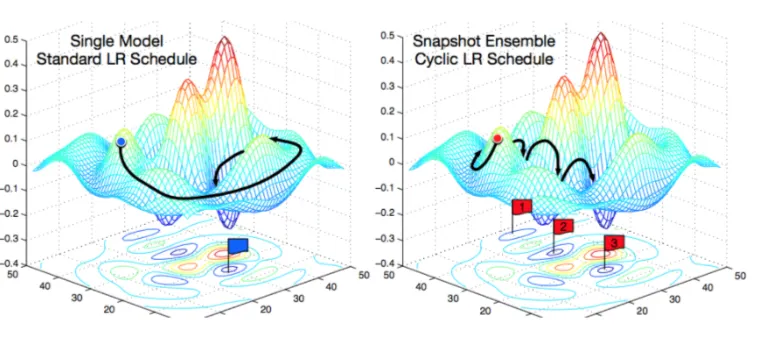
일반 lr scheduling과 cycle scheduling 방식의 차이
Made with