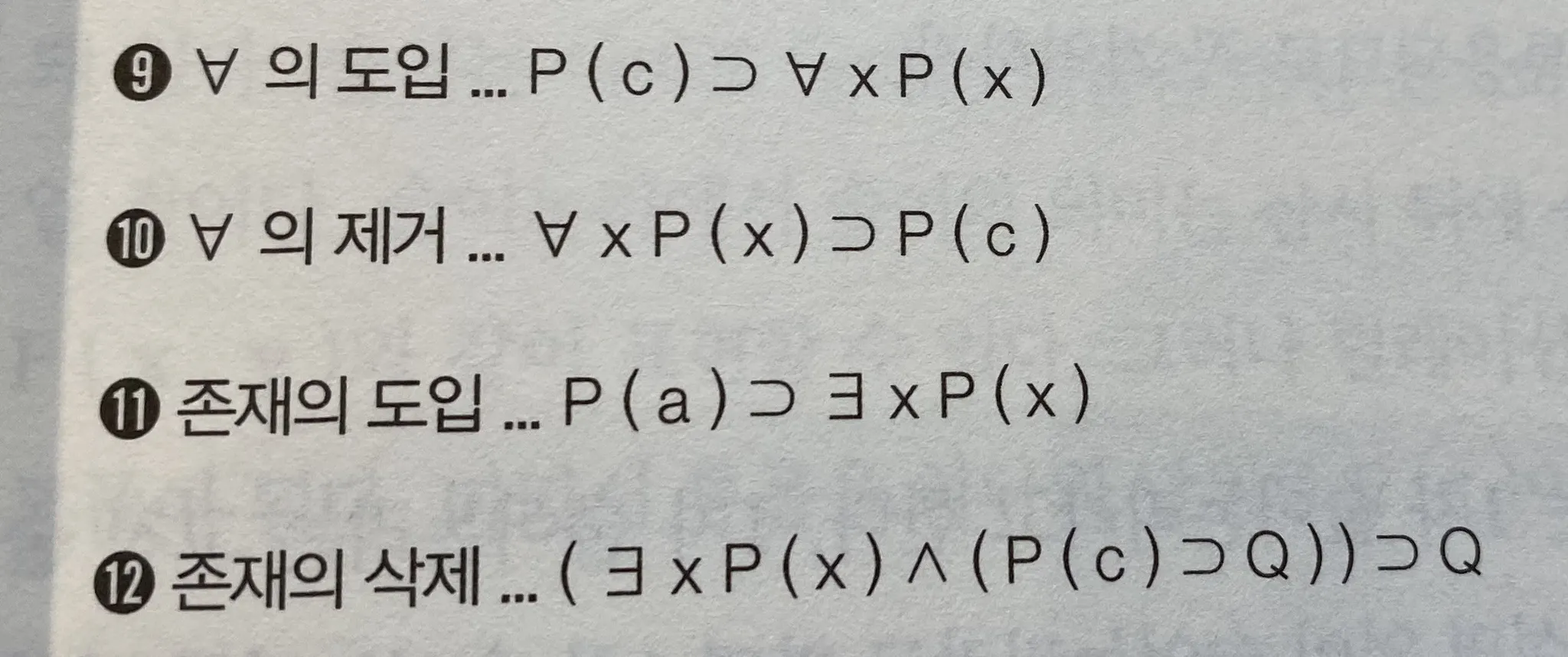관계형 모델 = 집합론을 기초로 한 데이터 모델 + 술어논리라는 논리학에 기초한 데이터 모델
술어논리 = 관계형 모델의 본질 → 정규화 & 정규화해야 하는 이유 이해에 필요
명제? 참인지 거짓인지 물을 수 있는 것 ex) 달은 행성이다. 타조는 날지 못한다.
명제논리? 어떤 명제(하나 or 여러개)의 참/거짓을 알고 있을 때 다른 명제의 참/거짓이 무엇인지 알아내는 데 특화된 학문
※ 명제논리에서 가장 중요한 점은 다른 명제의 참과 거짓 증명시 중요한 것은 명제들의 참/거짓 명제가 가진 다른 의미는 영향 xxxxx
(논리)연결자
복잡한 명제 ex) P이며 Q이다 = P라는 명제도 Q라는 명제도 둘 다 참이다 → '이며' : 연결자
대표적 논리 연결자들
1.
¬ (not)
2.
∧ (and)
3.
∨ (or)
4.
⊃(포함, IMP)
5.
≡ (동치, EQ)
6.
↑ (부정논리곱, NAND) → A NAND B = NOT (A AND B)
7.
↓ (부정논리합, NOR) → A NOR B = A NOR B = NOT (A OR B)
8.
⊻ (배타적 논리합, XOR)→ A XOR B = A'B+AB'
연결자 = 논리연산 :: 한가지 또는 두가지의 진리값으로 식 전체의 진리값을 고유하게 결정
→ 진리함수 → 진리표
동어 반복 & 정리
동어반복=항진식 식에 포함된 P, Q등의 명제의 값이 무엇이던지 전체의 참/거짓은 항상 참이 되는 경우
= 절대적인 법칙, 진리
어떤 설명이 바른지 아닌지 증명하거나, 참이 되는 논리식에서 다른 참이 되는 논리식 도출시에 사용
명제논리에서 동어 반복 = 정의 되어 있는 것
자주 사용되는 동어 반복으로는 동일법칙, 분배법칙, 드모르간 법칙 등이 있다.
명제논리와 공리계
한 서술을 참이라고 증명하고자 하면 참인 것을 보장하기 위한 전제가 되는 정리가 꼭 있어야 함
→ 어디까지 거슬러 올라가야 할까
공리
공리 = 아무런 전제 없이도 올바르다고 인정하자고 합의하에 정해진 다른 정리의 출발점
모든 정리의 출발점 = 공리
공리는
1.
하나뿐 아닌 여러 명제를 조합하여 성립
2.
공리로 정의된 명제끼리 모순이 있어선 안 됌 (무모순성)
3.
다뤄지는 주제가 전체를 포괄할 수 있음을 가정해 정의해야 함(완전성)
→ 이렇게 정한 공리의 집합 = 공리계
공리계의 예제
공리계 = 유일 x
무모순성/완전성 만족시키는 공리계는 몇몇 변종이 있을 수 있음 ( 명제논리도 마찬가지 )
명제논리의 공리계 중 대표적인 것 → 사실은 공리가 아닌 버전
공리는 정의되어 있지 않지만 기본적 4개의 연산자(¬, ∧, ∨, ⊃) 각각에 대해 도입/제거 위한 8가지의 도출규칙을 정의하여 공리계를 성립
(엄.....무슨말인지 모르겠음 사실... 그냥 논리연산시의 규칙..?이라고 생각하면 될 듯...)
어려운 3번(귀류법) 추가 설명
Q ^ ~Q? 말이 안 됌. 즉, 모순
명제 P는 참이라는 가정이 없으므로 P는 거짓이 되고 ~P가 참이 된다 (???)
→ 모순이 생기는 명제는 틀리다는 도출규칙 : 귀류법
공리계에는 증명의 도출점이 되는 공리가 없으므로 어떠한 가정을 도입하게 된다.
1.
P라는 가정 → 다른 명제 Q 도출 : 이 경우에는 1을 사용해 P ⊃ Q라는 명제 만들 수 있음.
2.
P라는 가정을 통해 모순되는 명제 Q ^ ~ Q 를 증명하면 3을 통해 ~P도출 가능
Principle of explosion 증명
(P ^ ~P) ⊃ Q
선언적 삼단논법이라는 다른 정리 사용
즉, Principle of explosion은 가정이 되는 명제에 모순이 있다면 어떤 결론도 도출할 수 없다는 것을 나타냄.
⇒ 공리계 자체에 모순이 있는 경우에도 마찬가지.
명제 논리의 한계와 양화논리(양한정)
세상에는 명제논리만으로 해결이 안되는 논리학적 문제 많음
명제논리의 한계
어떤 사실을 참/거짓을 가지는 명제로 표현하지 못 하는 경우도 있을 수 있음
ex) 이 마을의 모든 주민이 정직하다고 할 수 없다. → 어떤 논리식?
양화논리 : 집단을 대상으로 참고 거짓을 묻는 것
<술어논리에서의 양화논리 종류>
•
어떤 집단의 요소 전체가 어떠한 성질을 충족하는가? - 범용정량 ∀
•
어떤 집단의 요소는 어떠한 성질을 충족하는 것이 존재하는가? - 존재정량 ∃
정량자& 술어논리
이 마을의 주민은 모두 정직하다
→ x 는 정직하다 표현 함수 = F(x)라고 할 때, 이 마을의 주민은 모두 정직하다 = ∀ x F(x)
: 집단의 요소 전체(마을의 주민) 가 어떤 성질(정직함)을 충족한다는 것이니까.
이 마을에는 정직하지 않은 사람이 있다
→ ∃ x ¬ F(x)
: not F(x) = 정직하지 않음, 그리고 그런 사람이 있음을 ∃로 표현
: 집단의 요소(마을의 주민) 중 어떠한 성질(정직하지 않음)을 충족하는 것이 존재함.
정량자와 함께 사용하는 속박변수
왜 속박변수 일까? : 일반 변수처럼 보이지만 그 범위가 대상의 논리식 내로 한정되기 때문이다
ex) ∃ x F(x) ∧ ∀ x G(x) : x라는 공통 기호를 변수로 사용. 하지만 연결자 ∧ 앞 뒤 x의미가 다름 = 변수의 범위가 다름 = 정량자의 영향 범위에 속박되어 있음.
당연히 범용정량자의 영향범위와 존재정량자의 영향범위가 다르므로 속박변수 x의 의미가 다름
정량자를 사용하지 않는 자유변수
F(x)에서의 x는 변수지만 정량자를 사용하지 않는다 → 자유 변수
자유변수는 임의의 값을 얻을 때 정량자와 같은 범위에 속박되지 않음.
ex) F(x) ⊃ G(x)에서의 x는 모두 같은 x를 가리킴
그렇다면
F(x)처럼 자유변수를 포함한 식의 의미는?
→ x엔 임의의 값이 들어갈 가능성 O = x의 값 따라 F(x)의 값 바뀜
→ F(x)를 평가한 결과 = 참 또는 거짓
→ 자유변수를 인자로 받아 참 / 거짓을 반환하는 함수 = 명제함수
→ 명제함수 = 술어 = 주어가 되는 것이 변수 x고 함수 자체는 x대한 성질을 나타내기 때문
→ 술어를 이용한 논리 체계 = 술어논리
술어논리와 집합론
술어와 집합은 등가교환이 가능 = 술어를 집합으로 생각할 수 있음 = 집합을 술어로 생각할 수 있음
집합의 포함관계
SF는 SG의 subset(부분집합) & SG는 SF의 superset(상위 집합)
술어논리의 공리계
술어논리의 공리계 도출 규칙
= 앞에서의 명제논리와 공리계
+ 4가지 정량자 도출규칙
c = 임의의 값
※ P(c)는 임의의 값에 대해 보편적으로 P(x)가 성립한다는 의미
9 : 모든 값 대해 보편적으로 성립되는 규칙에서 범용기호를 통해 표현을 도출할 수 있다
10: 범용화된 술어는 임의의 값에 대해 성립되는 보편적 법칙이 도출되지 않아도 된다.
11: P(x) 를 만족하는 상수나 변수가 있으면 존재 정량자로 표현한 논리식을 도출해도 된다.
12: ∃ x P(x)라는 전제에 임의의 값 c에 대해 P(c) ⊃ Q라는 보편적 법칙이 성립한다면 Q라는 명제는 참이다.
! 근데 c가 임의의 값이라고 해서 정말 어떤 값을 대입해도 상관 없는 것은 아니다.
ex) 이 마을의 주민은 모두 정직하다고 할 수 없다 → 논의의 대상은 마을의 주민으로 한정
컵이나 꽃 이런 생명이 없는 것에 x는 정직하다는 술어를 적용할 수는 없다
→ 즉 술어논리는 논의의 대상이 되는 집합을 가정하는 것이 일반적이고, 이 집합을 도메인 이라고 한다.
도메인 개념은 (Domain of discourse) 관계형 모델에서도 통용됨
지금까지 소개한 술어논리 = 1차 술어논리 = 고전 술어논리
아무 설명 없이 술어논리라고 하면 1차 술어논리임.
1차 술어논리가 아닌 것 중 하나
2차 술어논리
술어의 특징을 표현하는 술어를 다룸
술어와 집합 = 1대1 대응
2차 술어 논리는 집합을 요소로 하는 집합을 다룸
1차 술어논리보다 표현할 수 있는 부분은 많으나 복잡함.
관계형 모델은 1차 술어논리를 바탕으로 디자인 된 데이터 모델
릴레이션의 참의 형태
릴레이션 = 집합
→ 집합은 1차 술어논리와 1대1 대응
→ 릴레이션에는 대응하는 술어가 존재