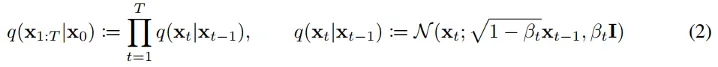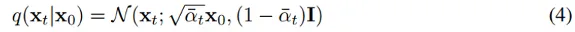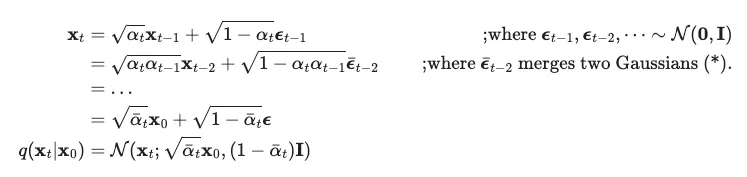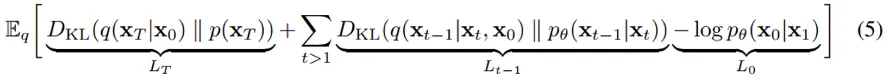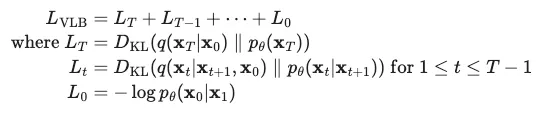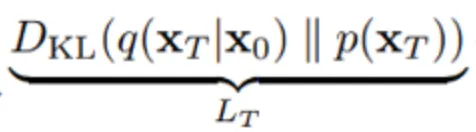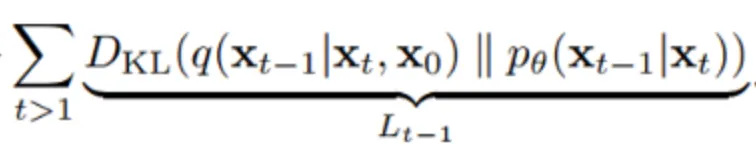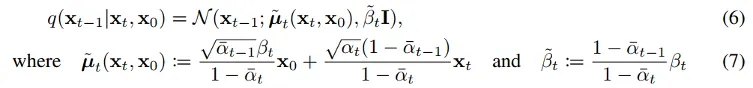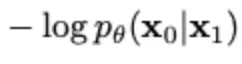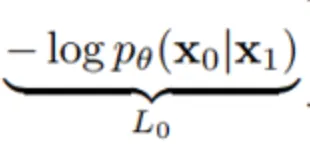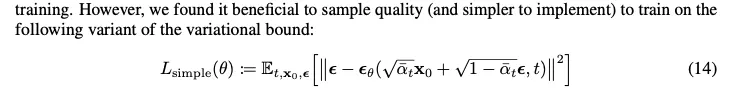//
Search
🔥

[diffusion model] Denoising Diffusion Probabilistic Models (Neurips 2020)

Denoising Diffusion Probabilistic Models
We present high quality image synthesis results using diffusion probabilistic models, a class of latent variable models inspired by considerations from nonequilibrium thermodynamics. Our best results are obtained by training on a weighted variational bound designed according to a novel connection between diffusion probabilistic models and denoising score matching with Langevin dynamics, and our models naturally admit a progressive lossy decompression scheme that can be interpreted as a generalization of autoregressive decoding.
https://arxiv.org/abs/2006.11239
요즘 Hot 한 diffusion model의 원조격인 논문이다. Novel ai 라는 곳에서 상용화하기도 한 모델이다. ( Stable Diffusion이라는 더 발전된 모델 ) 수식이 정말정말정말 많기 때문에 수식 하나하나를 다 이해하기 보다는 어떤 flow로 학습이 진행되는지, 기반이 되는 컨셉이 무엇인지, 구현은 어떤식으로 되어있는지 정도를 살펴보려고 한다.
기본적으로 diffusion model은 ‘생성’모델이다. 세상에 없는 어떤 새로운 것을 생성해내는 것이 목적이다.
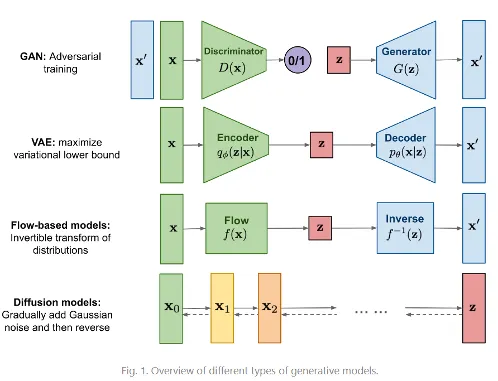
기존에 많이 사용되는 생성모델은 이렇게 4가지 정도로 추려볼 수 있다.
•
GAN
•
VAE
◦
관련 정리 자료 : VAE(Variational AutoEncoder)
•
Flow-based model
•
Diffusion model
•
최근 커뮤니티에서도 diffusion model이 성능이 좋다는 말이 많이 나오고 있고, 상용화도 되곤 하는 핫한 모델이다.
•
위 비교 그림에서 VAE와 Diffusion model을 비교해보면, VAE는 데이터의 분포를 잘 모델링한 latent variable z를 예측하는 방향으로 학습이 되지만, diffusion model은 데이터셋이 가지고 있는 multi-model distribution을 모델링하기 위해 gaussian noise를 활용한다.
•
GAN이나 VAE와 달리 latent space dimension이 input dimension과 동일하기 때문에 bottleneck구조에서 고려해야 하는 disentangled 속성이 없어서 DDPM은 좀 더 generative quality가 좋다고 할 수 있다. probabilistic model에 치중한 method이다.

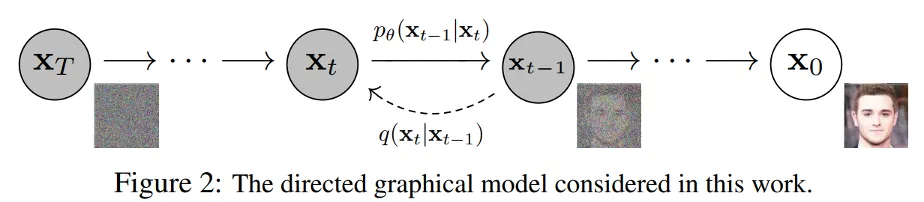
DDPM의 과정

논문에 첨부되어 있는 figure다. 기본적으로 x0→xT\bold{x}_0 → \bold{x}_T 과정을 forward process, xT→x0\bold{x}_T → \bold{x}_0 과정을 reverse process라고 정의한다. 주의할 점은 이 과정의 정의가 ‘training’과 관련된 것은 아니라는 것이다. 그냥 noise를 점점 더해주는 과정과 점점 없애주는 과정을 ‘용어로 정의’만 한 것 뿐이다.
timesteps는 보통 1000으로 정의한다. (github구현들)
•
Forward process : noise를 순차적으로 점점 더해주어 완전한 noise( 사람 그림의 의미가 완전히 깨질 때 까지 ) 로 만드는 과정. qq로 정의되어 있다.
◦
real data distribution에서 샘플링된 data point x0∼q(x)\bold{x}_0 \sim q(\bold{x}) 에 작은 Gaussian noise를 TT step만큼 더해준다. 그렇게 T개의 noisy samples를 생성한다. variance scheduling을 통해 step 당 더해줄 noise가 조절된다. {βt∈(0,1)}t=1T\{\beta_t \in (0, 1)\}_{t=1}^T linear하게 scheduling하기도 하고 cosine 함수의 일부분을 따서 하기도 한다.
◦
αt\alpha_t 를 통해 noise의 정도를 조절하며, 구현시 TT개만큼을 미리 정의해 둔다.
## pseudo code noise = torch.randn_like(x_0) # x_0의 size와 같은 gaussian 분포 생성 p_sample = sqrt(alpha_t)* x_0 + sqrt(1-alpha_t) * noise
Python
복사
이는 사실 reparameterization trick을 사용해 x0\bold{x}_0으로부터 xT\bold{x}_T를 생성해낸 것이다.
◦
αt=1−βt,      α‾t=∏t=1tαi\alpha_t = 1-\beta_t , \; \;\;\overline{\alpha}_t = \prod_{t=1}^t \alpha_i
두개의 분산이 다른 gaussian distribution을 더했을 때 ( 정규분포의 가법성 )
betas = torch.linspace(beta_start, beta_end, timesteps, dtype = torch.float64) # start값과 end값을 기준으로 step만큼의 값을 같은 간격으로 return alphas = 1. - betas alphas_cumprod = torch.cumprod(alphas, dim=0) # 누적곱을 return
Python
복사
•
Backward process : 완전한 noise 로부터 순차적으로 점점 original image로 복원해가는 과정. pθp_\theta 로 정의한다. q(xt−1∣xt)q(\bold{x}_{t-1}|\bold{x}_t) 를 예측하는 것이다. 그러나 이건 쉽지 않기 때문에 pθp_\theta 를 통해 conditional probabilities를 배워야 하는 것이다.
⇒ noise로부터 특정 시점 t의 noise xt\bold{x}_t를 예측
 reverse conditional probability는 x0\bold{x}_0 이 주어지면 다루기 쉽다 → q(xt−1∣xt,x0)=N(xt−1;μ~(xt,x0),β~tI)q(\bold{x}_{t-1}|\bold{x}_t, \bold{x}_0) = \mathcal{N}(\bold{x}_{t-1} ; \tilde{\mu}(\bold{x}_t, \bold{x}_0), \tilde{\beta}_t\bold{I})
p(xT)=N(xT;0,I)p(\bold{x}_T)=\mathcal{N}(\bold{x}_T;0, \bold{I}) 에서 시작하는 Markov chain with learned Gaussian transition으로 정의된 joint distribution pθ(x0:T)p_\theta(\bold{x}_{0:T})가 reverse process로 정의된다. ⇒ forward process에서 time step에 따라 추가된 gaussian noise의 평균과 분산을 알게 된다면 원래의 이미지 분포로 되돌아갈 수 있지 않을까?라는 개념인 듯 하다.
학습하는 과정을 보면 직관적으로 이해가 갈 것이다.

학습과정 (Loss)

Training과정은 usual variational bound on negative log likelihood를 optmizing하는 것으로 이루어진다.
여러 수식 정리를 통해 최종적으로 다음과 같은 형태로 정리된다.
이는 아래와 같이 KL divergence로 정리된다.
이 식은 실질적으로 사용되는 loss식이라기 보다는 이론적으로 나타낸 식이다.
LTL_T → forward process, t=Tt=T
p가 만드는 noisexT \bold{x}_T의 분포와 x0\bold{x}_0으로부터 q를 거쳐 만들어진 noise xT\bold{x}_T 사이의 KL divergence 를 최소화한다는 의미이다.
이 부분은 process를 많이 진행해 분모의 분포가 xT\bold{x}_T가 x0\bold{x}_0 과 독립적인 Gaussian distribution이라고 가정해 p도 Gaussian distribution에서 sampling하는 방식으로 여기서는 neural net이 학습되지 않는다.
그래서 구현을 보면 p로 들어가는 xTx_T input이 random하게 생성된다. ( torch.randn_like(x_0) )
L1:T−1L_{1:T-1}→ backward process, 1<t≤T1<t\leq T
1<t≤T1 < t \leq T 에 대한 pθ(xt−1∣xt)=N(xt−1;μθ(xt,t),∑θ(xt,t))p_\theta(\bold{x}_{t-1}|\bold{x}_t) = \mathcal{N}(\bold{x}_{t-1}; \bold{\mu}_\theta(\bold{x}_t, t), \sum_\theta(\bold{x}_t, t)) 의 선택에 대한 부분이다.
q가 gaussian process라면 reverse process는
다음과 같이 나타낼 수 있고 이로부터 위 loss term을 도출할 수 있다고 한다.
L0L_0 → Data scaling, reverse process decoder
VAE에서의 reconstruction loss와 같은 역할로, latent x1\bold{x}_1로부터 data인 x0\bold{x}_0을 추정하는 확률 모델의 parameter를 최적화하는 부분이다.
그러나 실제로 적용할 때에는 단순히 MSE Loss로 구현하였다. ( 식을 자세히 다루지 않은 이유… )
## p loss noise = torch.randn_like(x_0) x = q_t model = hybrid_Unet() p_t = model(x) target = noise loss = F.mse_loss(p_t, target)
Python
복사
## Training pseudo code for epoch in range(num_epochs): x_0 = next(dataloader).to(device) timesteps = 1000 timestep = torch.randint(1000) x_T = torch.randn_like(x_0) # 완전한 noise ( x_0과 관련 x ) x_t = q_sample(x_0, t=timestep) # q과정으로 t step의 x_0 + noise 이미지 추출 output = model(x_t, timestep) loss = p_loss(output, x_T) loss.backward()
Python
복사
이정도로 정리할 수 있을 것 같다.
그러니까 결과적으로 pθp_\theta (model) 에 p로 생성한 xt\bold{x}_t 가 들어가 생성한 noise와 랜덤하게 추출한 완전한 gaussian noise 사이의 차이를 줄이는 방향으로, input으로부터 생성된 noise로부터 완전한 noise를 만드는 것을 학습한다.
추가적인 training skills가 많이 있지만, 이 글에서는 DDPM의 기본적인 이론과 흐름만을 이해하는 것이 목표이기에 생략하겠다.

inference

inference는 다음과 같이 pseudo code를 살펴보면서 보는 것이 이해가 더 쉬울 듯 하다.
## Inference pseudo code ## 사전정의 beta와 alpha들 betas = torch.linspace(beta_start, beta_end, timesteps, dtype = torch.float64) # start값과 end값을 기준으로 step만큼의 값을 같은 간격으로 return alphas = 1. - betas alphas_cumprod = torch.cumprod(alphas, dim=0) # 누적곱을 return B, C, H, W = shape[:] img = torch.randn(shape, device=device) # 이부분은 사실 x_T를 지정하는 부분이라고 볼 수 있다. 무한한 timestep을 가정해 x_T는 x_0과 무관하다고 가정되기 때문이다. timesteps = torch.linspace(-1, T-1, steps=T+1) # [-1, 0, ..., T-1] timesteps = timesteps.int().tolist()[::-1] # [T-1, ..., -1] time_pairs = list(zip(timesteps[:-1], timesteps[1:])) # [(T-1, T-2), (T-2, T-3), ...., (1, 0), (0, -1)] for time, time_next in time_pars: target_time = torch.full((B, ), time) pred_noise = model(img, target_time) x_start = sqrt(1. / alphas_cumprod[time]) * img \ - sqrt(1./ alphas_cumprod[time] -1 )*pred_noise if time_next < 0 : img=x_0 continue alpha = alphas_cumprod[time] alpha_next = alphas_cumprod[time_next] sigma = ((1 - alpha / alpha_next) * (1 - alpha_next) / (1 - alpha)).sqrt() c = (1 - alpha_next - sigma ** 2).sqrt() noise = torch.randn_like(img) img = x_start * alpha_next.sqrt() + \ c * pred_noise + \ sigma * noise img = (img + 1) * 0.5 # [-1,1] -> [0, 1] return img
Python
복사
이 코드를 말로 설명해보겠다.
1.
일단 beta와 alpha값들은 timestep별로 미리 정의가 되어있다.
2.
img는 처음에 random한 gaussian noise로 정의된다. 이는 사실 xT\bold{x}_T를 의미한다. 왜냐하면 timesteps의 수가 큰 값이므로 무한한 것으로 가정하면서 xT\bold{x}_T는 x0\bold{x}_0과 관련 없는 독립적인 분포로 가정되기 때문이다.
3.
for문으로 들어가면서 xT−1\bold{x}_{T-1}부터 x0\bold{x}_0 까지를 순서대로 예측하게 된다. → 순차적으로 xt\bold{x}_t를 예측하는 과정
즉, xT\bold{x}_T로부터 xT−1\bold{x}_{T-1}을 예측하고, xT−1\bold{x}_{T-1}로부터 xT−2\bold{x}_{T-2}를 예측하고 … 반복하면서 마지막에 x1\bold{x}_1로부터 x0\bold{x}_0을 예측하게 된다. 이것이 우리가 원하는 최종 이미지가 되겠다.
4.
이렇게 각 xt \bold{x}_t를 예측할 때에, 보다싶이 수식이 들어간다.
•
model ( pθp_\theta )으로 예측한 pred_noise와 pred_noise를 이용해 예측한 x0\bold{x}_0 ( x_start )로부터 xt\bold{x}_t를 예측합니다.
•
xt\bold{x}_t 를 예측하는데에는 pp 에서 살펴보았던 reparameterization trick을 통해서xt \bold{x}_t가 x0\bold{x}_0과 ϵ\bold{\epsilon} 만으로 나타내지는 성질을 사용해 pred_noise와 x_start로 이루어진 수식으로 구현이 됩니다.
Made with